Beispiele für die Multiplikation gemischter Brüche. Regeln zum Multiplizieren von Brüchen mit Zahlen
§ 87. Addition von Brüchen.
Das Addieren von Brüchen hat viele Ähnlichkeiten mit dem Addieren ganzer Zahlen. Die Addition von Brüchen ist eine Aktion, die darin besteht, dass mehrere gegebene Zahlen (Terme) zu einer Zahl (Summe) zusammengefasst werden, die alle Einheiten und Brüche der Einheiten der Terme enthält.
Wir werden nacheinander drei Fälle betrachten:
1. Addition von Brüchen mit gleichen Nennern.
2. Addition von Brüchen mit unterschiedlichen Nennern.
3. Addition gemischter Zahlen.
1. Addition von Brüchen mit gleichen Nennern.
Betrachten Sie ein Beispiel: 1/5 + 2/5.
Nehmen wir das Segment AB (Abb. 17), nehmen Sie es als eins und teilen Sie es in 5 gleiche Teile, dann ist der Teil AC dieses Segments gleich 1/5 des Segments AB und der Teil desselben Segments CD ist gleich 2/5 AB.
Aus der Zeichnung geht hervor, dass, wenn wir das Segment AD nehmen, es gleich 3/5 AB ist; aber das Segment AD ist genau die Summe der Segmente AC und CD. Wir können also schreiben:
1 / 5 + 2 / 5 = 3 / 5
Wenn wir diese Terme und die resultierende Summe betrachten, sehen wir, dass der Zähler der Summe durch Addition der Zähler der Terme erhalten wurde und der Nenner unverändert blieb.
Daraus erhalten wir folgende Regel: Um Brüche mit demselben Nenner zu addieren, müssen Sie ihre Zähler addieren und denselben Nenner belassen.
Schauen wir uns ein Beispiel an:
2. Addition von Brüchen mit unterschiedlichen Nennern.
Addieren wir die Brüche: 3 / 4 + 3 / 8 Zuerst müssen sie auf den kleinsten gemeinsamen Nenner reduziert werden:
Der Zwischenlink 6/8 + 3/8 konnte nicht geschrieben werden; Aus Gründen der Klarheit haben wir es hier geschrieben.
Um Brüche mit unterschiedlichen Nennern zu addieren, müssen Sie sie zunächst auf den kleinsten gemeinsamen Nenner reduzieren, ihre Zähler addieren und den gemeinsamen Nenner beschriften.
Betrachten wir ein Beispiel (wir schreiben zusätzliche Faktoren über die entsprechenden Brüche):
3. Addition gemischter Zahlen.
Addieren wir die Zahlen: 2 3/8 + 3 5/6.
Bringen wir zunächst die Bruchteile unserer Zahlen auf einen gemeinsamen Nenner und schreiben sie noch einmal um:
![]()
Nun addieren wir nacheinander die ganzzahligen und gebrochenen Teile:
§ 88. Subtraktion von Brüchen.
Das Subtrahieren von Brüchen wird auf die gleiche Weise definiert wie das Subtrahieren ganzer Zahlen. Hierbei handelt es sich um eine Aktion, mit deren Hilfe aus der Summe zweier Terme und einem davon ein weiterer Term gefunden wird. Betrachten wir nacheinander drei Fälle:
1. Brüche mit gleichen Nennern subtrahieren.
2. Brüche mit unterschiedlichen Nennern subtrahieren.
3. Subtraktion gemischter Zahlen.
1. Brüche mit gleichen Nennern subtrahieren.
Schauen wir uns ein Beispiel an:
13 / 15 - 4 / 15
Nehmen wir das Segment AB (Abb. 18), nehmen es als Einheit und teilen es in 15 gleiche Teile; dann stellt der Teil AC dieses Segments 1/15 von AB dar und der Teil AD desselben Segments entspricht 13/15 AB. Lassen Sie uns ein weiteres Segment ED gleich 4/15 AB beiseite legen.
Wir müssen den Bruch 4/15 von 13/15 subtrahieren. In der Zeichnung bedeutet dies, dass das Segment ED vom Segment AD abgezogen werden muss. Dadurch bleibt das Segment AE erhalten, das 9/15 des Segments AB ausmacht. Wir können also schreiben:

Das von uns erstellte Beispiel zeigt, dass der Zähler der Differenz durch Subtrahieren der Zähler erhalten wurde, der Nenner jedoch derselbe blieb.
Um Brüche mit gleichen Nennern zu subtrahieren, müssen Sie daher den Zähler des Subtrahenden vom Zähler des Minuenden subtrahieren und den gleichen Nenner belassen.
2. Brüche mit unterschiedlichen Nennern subtrahieren.
Beispiel. 3/4 - 5/8
Lassen Sie uns zunächst diese Brüche auf den kleinsten gemeinsamen Nenner reduzieren:

Der Zwischentakt 6 / 8 - 5 / 8 ist hier der Übersichtlichkeit halber geschrieben, kann aber später übersprungen werden.
Um also einen Bruch von einem Bruch zu subtrahieren, müssen Sie diese zunächst auf den kleinsten gemeinsamen Nenner reduzieren, dann den Zähler des Minuenden vom Zähler des Minuenden subtrahieren und den gemeinsamen Nenner unter ihrer Differenz vorzeichen.
Schauen wir uns ein Beispiel an:
![]()
3. Subtraktion gemischter Zahlen.
Beispiel. 10 3/4 - 7 2/3.
Lassen Sie uns die Bruchteile von Minuend und Subtrahend auf den kleinsten gemeinsamen Nenner reduzieren:
Wir subtrahierten ein Ganzes von einem Ganzen und einen Bruch von einem Bruch. Es gibt jedoch Fälle, in denen der Nachkommateil des Subtrahends größer ist als der Nachkommateil des Minuenden. In solchen Fällen müssen Sie eine Einheit aus dem ganzen Teil des Minuends nehmen, sie in die Teile aufteilen, in denen der Bruchteil ausgedrückt wird, und sie zum Bruchteil des Minuends hinzufügen. Und dann wird die Subtraktion auf die gleiche Weise wie im vorherigen Beispiel durchgeführt:
§ 89. Multiplikation von Brüchen.
Beim Studium der Bruchmultiplikation werden wir die folgenden Fragen berücksichtigen:
1. Einen Bruch mit einer ganzen Zahl multiplizieren.
2. Ermitteln des Bruchteils einer bestimmten Zahl.
3. Eine ganze Zahl mit einem Bruch multiplizieren.
4. Einen Bruch mit einem Bruch multiplizieren.
5. Multiplikation gemischter Zahlen.
6. Der Begriff des Interesses.
7. Ermitteln des Prozentsatzes einer bestimmten Zahl. Betrachten wir sie der Reihe nach.
1. Einen Bruch mit einer ganzen Zahl multiplizieren.
Das Multiplizieren eines Bruchs mit einer ganzen Zahl hat die gleiche Bedeutung wie das Multiplizieren einer ganzen Zahl mit einer ganzen Zahl. Einen Bruch (Multiplikanden) mit einer ganzen Zahl (Faktor) zu multiplizieren bedeutet, eine Summe identischer Terme zu bilden, wobei jeder Term gleich dem Multiplikanden und die Anzahl der Terme gleich dem Multiplikator ist.
Das heißt, wenn Sie 1/9 mit 7 multiplizieren müssen, können Sie dies folgendermaßen tun:
Wir haben das Ergebnis leicht erhalten, da die Aktion auf das Addieren von Brüchen mit demselben Nenner reduziert wurde. Somit,
Die Betrachtung dieser Aktion zeigt, dass die Multiplikation eines Bruchs mit einer ganzen Zahl gleichbedeutend damit ist, diesen Bruch so oft zu erhöhen, wie es Einheiten in der ganzen Zahl gibt. Und da das Erhöhen eines Bruchs entweder durch Erhöhen seines Zählers erreicht wird
![]() oder durch Reduzierung seines Nenners
oder durch Reduzierung seines Nenners ![]() , dann können wir entweder den Zähler mit einer ganzen Zahl multiplizieren oder den Nenner durch diese dividieren, sofern eine solche Division möglich ist.
, dann können wir entweder den Zähler mit einer ganzen Zahl multiplizieren oder den Nenner durch diese dividieren, sofern eine solche Division möglich ist.
Von hier aus erhalten wir die Regel:
Um einen Bruch mit einer ganzen Zahl zu multiplizieren, multiplizieren Sie den Zähler mit dieser ganzen Zahl und lassen den Nenner gleich, oder dividieren, wenn möglich, den Nenner durch diese Zahl und lassen den Zähler unverändert.
Beim Multiplizieren sind Abkürzungen möglich, zum Beispiel:
2. Ermitteln des Bruchteils einer bestimmten Zahl. Es gibt viele Probleme, bei denen Sie einen Teil einer bestimmten Zahl finden oder berechnen müssen. Der Unterschied zwischen diesen Aufgaben und anderen besteht darin, dass sie die Anzahl einiger Objekte oder Maßeinheiten angeben und Sie einen Teil dieser Zahl finden müssen, der hier auch durch einen bestimmten Bruch angegeben wird. Um das Verständnis zu erleichtern, geben wir zunächst Beispiele für solche Probleme und stellen dann eine Methode zu deren Lösung vor.
Aufgabe 1. Ich hatte 60 Rubel; Ein Drittel dieses Geldes habe ich für den Kauf von Büchern ausgegeben. Wie viel haben die Bücher gekostet?
Aufgabe 2. Der Zug muss zwischen den Städten A und B eine Strecke von 300 km zurücklegen. Er hat bereits 2/3 dieser Strecke zurückgelegt. Wie viele Kilometer sind das?
Aufgabe 3. Es gibt 400 Häuser im Dorf, 3/4 davon sind aus Ziegeln, der Rest ist aus Holz. Wie viele Backsteinhäuser gibt es insgesamt?
Dies sind einige der vielen Probleme, auf die wir stoßen, wenn wir einen Teil einer bestimmten Zahl finden. Sie werden normalerweise als Probleme bezeichnet, um den Bruchteil einer bestimmten Zahl zu finden.
Lösung für Problem 1. Ab 60 Rubel. Ich habe 1/3 für Bücher ausgegeben; Das bedeutet, dass Sie die Zahl 60 durch 3 teilen müssen, um den Preis für Bücher zu ermitteln:
Lösung von Problem 2. Der Kern des Problems besteht darin, dass Sie 2/3 von 300 km finden müssen. Berechnen wir zunächst 1/3 von 300; Dies wird erreicht, indem man 300 km durch 3 teilt:
300: 3 = 100 (das ist 1/3 von 300).
Um zwei Drittel von 300 zu finden, müssen Sie den resultierenden Quotienten verdoppeln, also mit 2 multiplizieren:
100 x 2 = 200 (das sind 2/3 von 300).
Lösung von Problem 3. Hier müssen Sie die Anzahl der Backsteinhäuser bestimmen, die 3/4 von 400 ausmachen. Lassen Sie uns zunächst 1/4 von 400 ermitteln.
400: 4 = 100 (das ist 1/4 von 400).
Um drei Viertel von 400 zu berechnen, muss der resultierende Quotient verdreifacht, also mit 3 multipliziert werden:
100 x 3 = 300 (das sind 3/4 von 400).
Basierend auf der Lösung dieser Probleme können wir die folgende Regel ableiten:
Um den Wert eines Bruchs aus einer bestimmten Zahl zu ermitteln, müssen Sie diese Zahl durch den Nenner des Bruchs dividieren und den resultierenden Quotienten mit seinem Zähler multiplizieren.
3. Eine ganze Zahl mit einem Bruch multiplizieren.
Zuvor (§ 26) wurde festgelegt, dass unter der Multiplikation ganzer Zahlen die Addition identischer Terme zu verstehen ist (5 x 4 = 5+5 +5+5 = 20). In diesem Absatz (Punkt 1) wurde festgestellt, dass die Multiplikation eines Bruchs mit einer ganzen Zahl bedeutet, die Summe identischer Terme zu finden, die diesem Bruch entspricht.
In beiden Fällen bestand die Multiplikation darin, die Summe identischer Terme zu ermitteln.
Jetzt gehen wir dazu über, eine ganze Zahl mit einem Bruch zu multiplizieren. Hier stoßen wir zum Beispiel auf die Multiplikation: 9 2 / 3. Es ist klar, dass die vorherige Definition der Multiplikation auf diesen Fall nicht anwendbar ist. Dies wird aus der Tatsache deutlich, dass wir eine solche Multiplikation nicht durch Addition gleicher Zahlen ersetzen können.
Aus diesem Grund müssen wir die Multiplikation neu definieren, also mit anderen Worten die Frage beantworten, was unter Multiplikation mit einem Bruch zu verstehen ist und wie diese Aktion zu verstehen ist.
Die Bedeutung der Multiplikation einer ganzen Zahl mit einem Bruch wird aus der folgenden Definition deutlich: Eine ganze Zahl (Multiplikand) mit einem Bruch (Multiplikand) zu multiplizieren bedeutet, diesen Bruchteil des Multiplikanden zu finden.
Das heißt, 9 mit 2/3 zu multiplizieren bedeutet, 2/3 von neun Einheiten zu finden. Im vorherigen Absatz wurden solche Probleme gelöst; Es ist also leicht herauszufinden, dass wir am Ende bei 6 landen.
Doch nun stellt sich eine interessante und wichtige Frage: Warum werden solche scheinbar unterschiedlichen Operationen, wie das Ermitteln der Summe gleicher Zahlen und das Ermitteln des Bruchteils einer Zahl, in der Arithmetik mit demselben Wort „Multiplikation“ genannt?
Dies geschieht, weil die vorherige Aktion (mehrmaliges Wiederholen einer Zahl mit Begriffen) und die neue Aktion (Ermitteln des Bruchteils einer Zahl) Antworten auf homogene Fragen geben. Das heißt, wir gehen hier von der Überlegung aus, dass homogene Fragestellungen oder Aufgaben durch die gleiche Handlung gelöst werden.
Um dies zu verstehen, betrachten Sie das folgende Problem: „1 m Stoff kostet 50 Rubel. Wie viel kosten 4 m eines solchen Stoffes?
Dieses Problem wird gelöst, indem man die Anzahl der Rubel (50) mit der Anzahl der Meter (4) multipliziert, also 50 x 4 = 200 (Rubel).
Nehmen wir das gleiche Problem, aber darin wird die Stoffmenge als Bruchteil ausgedrückt: „1 m Stoff kostet 50 Rubel. Wie viel werden 3/4 m dieses Stoffes kosten?“
Dieses Problem muss auch gelöst werden, indem die Anzahl der Rubel (50) mit der Anzahl der Meter (3/4) multipliziert wird.
Sie können die darin enthaltenen Zahlen noch mehrmals ändern, ohne die Bedeutung der Aufgabe zu ändern, z. B. 9/10 m oder 2 3/10 m usw.
Da diese Probleme den gleichen Inhalt haben und sich nur in der Zahl unterscheiden, nennen wir die zu ihrer Lösung verwendeten Aktionen das gleiche Wort – Multiplikation.
Wie multipliziert man eine ganze Zahl mit einem Bruch?
Nehmen wir die im letzten Problem gefundenen Zahlen:
Laut Definition müssen wir 3/4 von 50 finden. Finden wir zuerst 1/4 von 50 und dann 3/4.
1/4 von 50 ist 50/4;
3/4 der Zahl 50 ist .
Somit.
Betrachten wir ein anderes Beispiel: 12 5 / 8 =?
1/8 der Zahl 12 ist 12/8,
5/8 der Zahl 12 ist .
Somit,
Von hier aus erhalten wir die Regel:
Um eine ganze Zahl mit einem Bruch zu multiplizieren, müssen Sie die ganze Zahl mit dem Zähler des Bruchs multiplizieren, dieses Produkt zum Zähler machen und den Nenner dieses Bruchs als Nenner vorzeichen.
Schreiben wir diese Regel mit Buchstaben:
Um diese Regel vollständig zu verdeutlichen, sollte man bedenken, dass ein Bruch als Quotient betrachtet werden kann. Daher ist es sinnvoll, die gefundene Regel mit der in § 38 dargelegten Regel zur Multiplikation einer Zahl mit einem Quotienten zu vergleichen
Es ist wichtig, sich daran zu erinnern, dass Sie (wenn möglich) vor der Multiplikation Folgendes tun sollten: Ermäßigungen, Zum Beispiel:
4. Einen Bruch mit einem Bruch multiplizieren. Das Multiplizieren eines Bruchs mit einem Bruch hat die gleiche Bedeutung wie das Multiplizieren einer ganzen Zahl mit einem Bruch, d. h. wenn Sie einen Bruch mit einem Bruch multiplizieren, müssen Sie den Bruch ermitteln, der im Faktor des ersten Bruchs (dem Multiplikanden) enthalten ist.
Das heißt, die Multiplikation von 3/4 mit 1/2 (die Hälfte) bedeutet, die Hälfte von 3/4 zu finden.
Wie multipliziert man einen Bruch mit einem Bruch?
Nehmen wir ein Beispiel: 3/4 multipliziert mit 5/7. Das bedeutet, dass Sie 5/7 von 3/4 finden müssen. Finden wir zuerst 1/7 von 3/4 und dann 5/7
1/7 der Zahl 3/4 wird wie folgt ausgedrückt:
5/7 Zahlen 3/4 werden wie folgt ausgedrückt:
Auf diese Weise,
![]()
Ein weiteres Beispiel: 5/8 multipliziert mit 4/9.
1/9 von 5/8 ist,
4/9 der Zahl 5/8 ist .
Auf diese Weise, ![]()
Aus diesen Beispielen lässt sich folgende Regel ableiten:
Um einen Bruch mit einem Bruch zu multiplizieren, müssen Sie den Zähler mit dem Zähler und den Nenner mit dem Nenner multiplizieren und das erste Produkt zum Zähler und das zweite Produkt zum Nenner des Produkts machen.
Diese Regel kann in allgemeiner Form wie folgt geschrieben werden:
![]()
Bei der Multiplikation müssen (wenn möglich) Kürzungen vorgenommen werden. Schauen wir uns Beispiele an:

5. Multiplikation gemischter Zahlen. Da gemischte Zahlen leicht durch unechte Brüche ersetzt werden können, wird dieser Umstand meist bei der Multiplikation gemischter Zahlen genutzt. Das bedeutet, dass in den Fällen, in denen der Multiplikand oder der Multiplikator oder beide Faktoren als gemischte Zahlen ausgedrückt werden, diese durch unechte Brüche ersetzt werden. Lassen Sie uns zum Beispiel gemischte Zahlen multiplizieren: 2 1/2 und 3 1/5. Lassen Sie uns jeden von ihnen in einen unechten Bruch umwandeln und dann die resultierenden Brüche gemäß der Regel zum Multiplizieren eines Bruchs mit einem Bruch multiplizieren:
Regel. Um gemischte Zahlen zu multiplizieren, müssen Sie sie zunächst in unechte Brüche umwandeln und diese dann gemäß der Regel zum Multiplizieren von Brüchen mit Brüchen multiplizieren.
Notiz. Ist einer der Faktoren eine ganze Zahl, dann kann die Multiplikation nach dem Verteilungsgesetz wie folgt durchgeführt werden:
6. Der Begriff des Interesses. Beim Lösen von Problemen und bei der Durchführung verschiedener praktischer Berechnungen verwenden wir alle Arten von Brüchen. Es muss jedoch berücksichtigt werden, dass viele Größen nicht irgendwelche, sondern natürliche Unterteilungen zulassen. Sie können zum Beispiel ein Hundertstel (1/100) eines Rubels nehmen, es wird eine Kopeke sein, zwei Hundertstel sind 2 Kopeken, drei Hundertstel sind 3 Kopeken. Sie können 1/10 eines Rubels nehmen, es sind „10 Kopeken“ oder ein Zehn-Kopeken-Stück. Sie können einen viertel Rubel nehmen, also 25 Kopeken, einen halben Rubel, also 50 Kopeken (fünfzig Kopeken). Aber Sie nehmen es praktisch nicht, zum Beispiel 2/7 eines Rubels, weil der Rubel nicht in Siebtel unterteilt ist.
Bei der Gewichtseinheit Kilogramm sind vor allem Dezimalteilungen möglich, zum Beispiel 1/10 kg oder 100 g. Auch Bruchteile eines Kilogramms wie 1/6, 1/11, 1/13 sind nicht üblich.
Im Allgemeinen sind unsere (metrischen) Maße dezimal und erlauben Dezimalteilungen.
Es ist jedoch zu beachten, dass es in den unterschiedlichsten Fällen äußerst nützlich und praktisch ist, die gleiche (einheitliche) Methode zur Unterteilung von Mengen zu verwenden. Die langjährige Erfahrung hat gezeigt, dass eine solche wohlbegründete Teilung die „hundertste“ Teilung ist. Betrachten wir einige Beispiele aus den unterschiedlichsten Bereichen menschlicher Praxis.
1. Der Preis für Bücher ist um 12/100 des vorherigen Preises gesunken.
Beispiel. Der vorherige Preis des Buches betrug 10 Rubel. Es verringerte sich um 1 Rubel. 20 Kopeken
2. Sparkassen zahlen den Einlegern 2/100 des im Laufe des Jahres eingezahlten Sparbetrags.
Beispiel. 500 Rubel werden in die Kasse eingezahlt, der Jahreserlös aus diesem Betrag beträgt 10 Rubel.
3. Die Zahl der Absolventen einer Schule betrug 5/100 der Gesamtzahl der Schüler.
BEISPIEL Es gab nur 1.200 Schüler an der Schule, von denen 60 ihren Abschluss machten.
Der Hundertstelteil einer Zahl wird als Prozentsatz bezeichnet.
Das Wort „Prozent“ ist dem Lateinischen entlehnt und seine Wurzel „Cent“ bedeutet einhundert. Zusammen mit der Präposition (pro centum) bedeutet dieses Wort „für hundert“. Die Bedeutung eines solchen Ausdrucks ergibt sich aus der Tatsache, dass zunächst in antikes Rom Zinsen waren das Geld, das der Schuldner dem Kreditgeber „pro Hundert“ zahlte. Das Wort „Cent“ hört man in so vertrauten Worten: Centner (einhundert Kilogramm), Centimeter (sagen wir Zentimeter).
Anstatt beispielsweise zu sagen, dass das Werk im letzten Monat 1/100 aller von ihm hergestellten Produkte fehlerhaft war, sagen wir Folgendes: Im vergangenen Monat produzierte das Werk ein Prozent der von ihm hergestellten Produkte. Anstatt zu sagen: Das Werk hat 4/100 Produkte mehr produziert als der festgelegte Plan, sagen wir: Das Werk hat den Plan um 4 Prozent übertroffen.
Die obigen Beispiele können unterschiedlich ausgedrückt werden:
1. Der Preis für Bücher ist um 12 Prozent des vorherigen Preises gesunken.
2. Sparkassen zahlen den Einlegern jährlich 2 Prozent auf den eingezahlten Sparbetrag.
3. Die Zahl der Absolventen einer Schule betrug 5 Prozent aller Schüler.
Um den Buchstaben zu verkürzen, ist es üblich, anstelle des Wortes „Prozentsatz“ das %-Symbol zu schreiben.
Sie müssen jedoch bedenken, dass das %-Zeichen in Berechnungen normalerweise nicht geschrieben wird; es kann in der Problemstellung und im Endergebnis geschrieben werden. Bei Berechnungen müssen Sie mit diesem Symbol einen Bruch mit dem Nenner 100 anstelle einer ganzen Zahl schreiben.
Sie müssen in der Lage sein, eine ganze Zahl mit dem angegebenen Symbol durch einen Bruch mit dem Nenner 100 zu ersetzen:
Umgekehrt müssen Sie sich daran gewöhnen, eine ganze Zahl mit dem angegebenen Symbol anstelle eines Bruchs mit dem Nenner 100 zu schreiben:
7. Ermitteln des Prozentsatzes einer bestimmten Zahl.
Aufgabe 1. Die Schule erhielt 200 Kubikmeter. m Brennholz, davon 30 % Birkenbrennholz. Wie viel Birkenbrennholz gab es?
Die Bedeutung dieses Problems besteht darin, dass Birkenbrennholz nur einen Teil des an die Schule gelieferten Brennholzes ausmachte und dieser Teil im Bruchteil 30/100 ausgedrückt wird. Das bedeutet, dass wir die Aufgabe haben, den Bruchteil einer Zahl zu finden. Um es zu lösen, müssen wir 200 mit 30/100 multiplizieren (Probleme, den Bruch einer Zahl zu finden, werden gelöst, indem man die Zahl mit dem Bruch multipliziert).
Das bedeutet, dass 30 % von 200 60 ergeben.
Der in diesem Problem vorkommende Bruch 30/100 kann um 10 reduziert werden. Es wäre möglich, diese Reduzierung von Anfang an vorzunehmen; an der Lösung des Problems hätte sich nichts geändert.
Aufgabe 2. Im Lager befanden sich 300 Kinder unterschiedlichen Alters. Kinder im Alter von 11 Jahren machten 21 % aus, Kinder im Alter von 12 Jahren machten 61 % aus und schließlich machten Kinder im Alter von 13 Jahren 18 % aus. Wie viele Kinder jeden Alters gab es im Lager?
Bei dieser Aufgabe müssen Sie drei Berechnungen durchführen, d. h. nacheinander die Anzahl der Kinder im Alter von 11 Jahren, dann im Alter von 12 Jahren und schließlich im Alter von 13 Jahren ermitteln.
Das bedeutet, dass Sie hier dreimal den Bruchteil der Zahl ermitteln müssen. Lass es uns tun:
1) Wie viele 11-jährige Kinder gab es?
2) Wie viele 12-jährige Kinder gab es?
3) Wie viele 13-jährige Kinder gab es?
Nach Lösung des Problems ist es sinnvoll, die gefundenen Zahlen zu addieren; ihre Summe sollte 300 betragen:
63 + 183 + 54 = 300
Es ist auch zu beachten, dass die Summe der in der Problemstellung angegebenen Prozentsätze 100 beträgt:
21% + 61% + 18% = 100%
Das deutet darauf hin Gesamtzahl Kinder im Lager wurden zu 100 % berücksichtigt.
3 a d a h a 3. Der Arbeiter erhielt 1.200 Rubel pro Monat. Davon gab er 65 % für Lebensmittel, 6 % für Wohnungen und Heizung, 4 % für Gas, Strom und Radio, 10 % für kulturelle Zwecke und 15 % für Ersparnisse aus. Wie viel Geld wurde für die im Problem angegebenen Bedürfnisse ausgegeben?
Um dieses Problem zu lösen, müssen Sie den Bruchteil von 1.200 fünfmal ermitteln. Lassen Sie uns Folgendes tun.
1) Wie viel Geld wurde für Lebensmittel ausgegeben? Das Problem besagt, dass dieser Aufwand 65 % des Gesamteinkommens ausmacht, also 65/100 der Zahl 1.200. Machen wir die Rechnung:
![]()
2) Wie viel Geld haben Sie für eine Wohnung mit Heizung bezahlt? Wenn wir ähnlich wie zuvor argumentieren, kommen wir zu folgender Berechnung:
3) Wie viel Geld haben Sie für Gas, Strom und Radio bezahlt?
4) Wie viel Geld wurde für kulturelle Zwecke ausgegeben?
5) Wie viel Geld hat der Arbeitnehmer gespart?
Um dies zu überprüfen, ist es sinnvoll, die in diesen 5 Fragen gefundenen Zahlen zu addieren. Der Betrag sollte 1.200 Rubel betragen. Alle Einnahmen werden als 100 % angenommen, was sich leicht überprüfen lässt, indem man die in der Problemstellung angegebenen Prozentzahlen addiert.
Wir haben drei Probleme gelöst. Obwohl es sich bei diesen Problemen um unterschiedliche Dinge handelte (Lieferung von Brennholz für die Schule, Anzahl der Kinder unterschiedlichen Alters, Kosten des Arbeiters), wurden sie auf die gleiche Weise gelöst. Dies geschah, weil es bei allen Aufgaben notwendig war, mehrere Prozent der gegebenen Zahlen zu finden.
§ 90. Division von Brüchen.
Während wir uns mit der Division von Brüchen befassen, werden wir die folgenden Fragen berücksichtigen:
1. Teilen Sie eine ganze Zahl durch eine ganze Zahl.
2. Einen Bruch durch eine ganze Zahl dividieren
3. Eine ganze Zahl durch einen Bruch dividieren.
4. Einen Bruch durch einen Bruch dividieren.
5. Division gemischter Zahlen.
6. Finden einer Zahl aus ihrem gegebenen Bruch.
7. Eine Zahl anhand ihres Prozentsatzes ermitteln.
Betrachten wir sie der Reihe nach.
1. Teilen Sie eine ganze Zahl durch eine ganze Zahl.
Wie bereits in der Abteilung für ganze Zahlen erwähnt, ist Division die Aktion, die darin besteht, dass aus dem Produkt zweier Faktoren (Dividende) und einem dieser Faktoren (Divisor) ein anderer Faktor gefunden wird.
Wir haben uns im Abschnitt über ganze Zahlen mit der Division einer ganzen Zahl durch eine ganze Zahl befasst. Wir sind dort auf zwei Fälle von Division gestoßen: Division ohne Rest oder „ganz“ (150: 10 = 15) und Division mit Rest (100: 9 = 11 und 1 Rest). Wir können daher sagen, dass im Bereich der ganzen Zahlen eine exakte Division nicht immer möglich ist, da der Dividend nicht immer das Produkt des Divisors durch die ganze Zahl ist. Nachdem wir die Multiplikation mit einem Bruch eingeführt haben, können wir jeden Fall der Division von ganzen Zahlen als möglich betrachten (nur die Division durch Null ist ausgeschlossen).
Wenn man beispielsweise 7 durch 12 dividiert, findet man eine Zahl, deren Produkt durch 12 7 ergibt. Eine solche Zahl ist der Bruch 7 / 12, weil 7 / 12 · 12 = 7. Ein weiteres Beispiel: 14: 25 = 14 / 25, weil 14 / 25 25 = 14.
Um also eine ganze Zahl durch eine ganze Zahl zu dividieren, müssen Sie einen Bruch bilden, dessen Zähler gleich dem Dividenden und dessen Nenner gleich dem Divisor ist.
2. Einen Bruch durch eine ganze Zahl dividieren.
Teilen Sie den Bruch 6 / 7 durch 3. Gemäß der oben gegebenen Divisionsdefinition haben wir hier das Produkt (6 / 7) und einen der Faktoren (3); Es ist erforderlich, einen zweiten Faktor zu finden, der bei Multiplikation mit 3 das gegebene Produkt 6/7 ergeben würde. Offensichtlich sollte es dreimal kleiner sein als dieses Produkt. Das bedeutet, dass die vor uns liegende Aufgabe darin bestand, den Bruch 6/7 um das Dreifache zu reduzieren.
Wir wissen bereits, dass die Reduzierung eines Bruchs entweder durch Verringern seines Zählers oder durch Erhöhen seines Nenners erfolgen kann. Daher können Sie schreiben:
![]()
IN in diesem Fall Der Zähler von 6 ist durch 3 teilbar, daher sollte der Zähler halbiert werden.
Nehmen wir ein anderes Beispiel: 5 / 8 geteilt durch 2. Hier ist der Zähler 5 nicht durch 2 teilbar, was bedeutet, dass der Nenner mit dieser Zahl multipliziert werden muss:
![]()
Darauf aufbauend lässt sich eine Regel aufstellen: Um einen Bruch durch eine ganze Zahl zu dividieren, müssen Sie den Zähler des Bruchs durch diese ganze Zahl dividieren.(wenn möglich), Belassen Sie den gleichen Nenner oder multiplizieren Sie den Nenner des Bruchs mit dieser Zahl und lassen Sie den gleichen Zähler übrig.
3. Eine ganze Zahl durch einen Bruch dividieren.
Es sei notwendig, 5 durch 1/2 zu dividieren, d. h. eine Zahl zu finden, die nach Multiplikation mit 1/2 das Produkt 5 ergibt. Offensichtlich muss diese Zahl größer als 5 sein, da 1/2 ein echter Bruch ist , und beim Multiplizieren einer Zahl muss das Produkt eines echten Bruchs kleiner sein als das zu multiplizierende Produkt. Um dies klarer zu machen, schreiben wir unsere Aktionen wie folgt: 5: 1 / 2 = X , was x 1 / 2 = 5 bedeutet.
Wir müssen eine solche Zahl finden X , was, wenn es mit 1/2 multipliziert würde, 5 ergeben würde. Da das Multiplizieren einer bestimmten Zahl mit 1/2 bedeutet, die Hälfte dieser Zahl zu finden, dann also die Hälfte der unbekannten Zahl X ist gleich 5 und die ganze Zahl X doppelt so viel, also 5 2 = 10.
Also 5: 1 / 2 = 5 · 2 = 10
Lass uns das Prüfen: ![]()
Schauen wir uns ein anderes Beispiel an. Nehmen wir an, Sie möchten 6 durch 2/3 teilen. Versuchen wir zunächst anhand der Zeichnung (Abb. 19) das gewünschte Ergebnis zu finden.
Abb.19
Zeichnen wir ein Segment AB mit 6 Einheiten und teilen wir jede Einheit in 3 gleiche Teile. In jeder Einheit sind drei Drittel (3/3) des gesamten Segments AB sechsmal größer, d. h. B. 18/3. Mit kleinen Klammern verbinden wir die 18 resultierenden Segmente von 2; Es wird nur 9 Segmente geben. Das bedeutet, dass der Bruch 2/3 9-mal in 6 Einheiten enthalten ist, oder anders ausgedrückt, der Bruch 2/3 ist 9-mal kleiner als 6 ganze Einheiten. Somit,
Wie kommt man zu diesem Ergebnis ohne eine Zeichnung allein durch Berechnungen? Lassen Sie uns so argumentieren: Wir müssen 6 durch 2/3 dividieren, d. h. wir müssen die Frage beantworten, wie oft 2/3 in 6 enthalten ist. Lassen Sie uns zunächst herausfinden: Wie oft ist 1/3 in 6 enthalten? In einer ganzen Einheit gibt es 3 Drittel, und in 6 Einheiten sind es 6 mal mehr, also 18 Drittel; Um diese Zahl zu finden, müssen wir 6 mit 3 multiplizieren. Das bedeutet, dass 1/3 18-mal in b-Einheiten enthalten ist und 2/3 nicht 18-mal, sondern halb so oft in b-Einheiten enthalten ist, also 18:2 = 9 Deshalb haben wir bei der Division von 6 durch 2/3 Folgendes getan:
![]()
Von hier aus erhalten wir die Regel zum Teilen einer ganzen Zahl durch einen Bruch. Um eine ganze Zahl durch einen Bruch zu dividieren, müssen Sie diese ganze Zahl mit dem Nenner des gegebenen Bruchs multiplizieren und dieses Produkt zum Zähler machen und es durch den Zähler des gegebenen Bruchs dividieren.
Schreiben wir die Regel mit Buchstaben:
Um diese Regel vollständig zu verdeutlichen, sollte man bedenken, dass ein Bruch als Quotient betrachtet werden kann. Daher ist es sinnvoll, die gefundene Regel mit der in § 38 dargelegten Regel zur Division einer Zahl durch einen Quotienten zu vergleichen. Bitte beachten Sie, dass dort die gleiche Formel erhalten wurde.
Beim Dividieren sind Abkürzungen möglich, zum Beispiel:
4. Einen Bruch durch einen Bruch dividieren.
Nehmen wir an, wir müssen 3/4 durch 3/8 teilen. Was bedeutet die Zahl, die sich aus der Division ergibt? Es wird die Frage beantworten, wie oft der Bruch 3/8 im Bruch 3/4 enthalten ist. Um dieses Problem zu verstehen, erstellen wir eine Zeichnung (Abb. 20).

Nehmen wir ein Segment AB, nehmen es als Ganzes, teilen es in 4 gleiche Teile und markieren 3 solcher Teile. Segment AC entspricht 3/4 von Segment AB. Teilen wir nun jedes der vier ursprünglichen Segmente in zwei Hälften, dann wird das Segment AB in 8 gleiche Teile geteilt und jeder dieser Teile entspricht 1/8 des Segments AB. Verbinden wir 3 solcher Segmente mit Bögen, dann ist jedes der Segmente AD und DC gleich 3/8 des Segments AB. Die Zeichnung zeigt, dass ein Segment gleich 3/8 genau zweimal in einem Segment gleich 3/4 enthalten ist; Das bedeutet, dass das Ergebnis der Division wie folgt geschrieben werden kann:
3 / 4: 3 / 8 = 2
Schauen wir uns ein anderes Beispiel an. Nehmen wir an, wir müssen 15/16 durch 3/32 teilen:
Wir können so argumentieren: Wir müssen eine Zahl finden, die nach Multiplikation mit 3/32 ein Produkt von 15/16 ergibt. Schreiben wir die Berechnungen so:
15 / 16: 3 / 32 = X
3 / 32 X = 15 / 16
3/32 unbekannte Nummer X sind 15/16
1/32 einer unbekannten Zahl X Ist ,
32 / 32 Zahlen X bilden .
Somit,
![]()
Um also einen Bruch durch einen Bruch zu dividieren, müssen Sie den Zähler des ersten Bruchs mit dem Nenner des zweiten multiplizieren und den Nenner des ersten Bruchs mit dem Zähler des zweiten multiplizieren und das erste Produkt zum Zähler machen. und der zweite der Nenner.
Schreiben wir die Regel mit Buchstaben:
Beim Dividieren sind Abkürzungen möglich, zum Beispiel:
5. Division gemischter Zahlen.
Bei der Division gemischter Zahlen müssen diese zunächst in unechte Brüche umgewandelt werden und anschließend müssen die resultierenden Brüche gemäß den Regeln für die Division von Brüchen dividiert werden. Schauen wir uns ein Beispiel an:
Lassen Sie uns gemischte Zahlen in unechte Brüche umwandeln:
![]()
Teilen wir nun:
Um gemischte Zahlen zu dividieren, müssen Sie sie also in unechte Brüche umwandeln und dann mit der Regel zum Dividieren von Brüchen dividieren.
6. Finden einer Zahl aus ihrem gegebenen Bruch.
Unter den verschiedenen Bruchproblemen gibt es manchmal solche, bei denen der Wert eines Bruchs einer unbekannten Zahl angegeben ist und Sie diese Zahl finden müssen. Diese Art von Problem ist die Umkehrung des Problems, den Bruchteil einer gegebenen Zahl zu finden; dort wurde eine Zahl angegeben und es galt, einen Bruchteil dieser Zahl zu finden, hier wurde ein Bruchteil einer Zahl angegeben und es galt, diese Zahl selbst zu finden. Diese Idee wird noch deutlicher, wenn wir uns der Lösung dieser Art von Problemen zuwenden.
Aufgabe 1. Am ersten Tag verglasten die Glaser 50 Fenster, also 1/3 aller Fenster des gebauten Hauses. Wie viele Fenster gibt es in diesem Haus?
Lösung. Das Problem besagt, dass 50 verglaste Fenster 1/3 aller Fenster des Hauses ausmachen, was bedeutet, dass insgesamt dreimal mehr Fenster vorhanden sind, d. h.
Das Haus hatte 150 Fenster.
Aufgabe 2. Der Laden verkaufte 1.500 kg Mehl, was 3/8 des gesamten Mehlvorrats des Ladens entspricht. Wie hoch war der anfängliche Mehlvorrat des Geschäfts?
Lösung. Aus der Problemlage geht hervor, dass 1.500 kg verkauftes Mehl 3/8 des Gesamtbestandes ausmachen; Das bedeutet, dass 1/8 dieser Reserve dreimal weniger ist, d. h. um sie zu berechnen, müssen Sie 1500 um das Dreifache reduzieren:
1.500: 3 = 500 (das ist 1/8 der Reserve).
Offensichtlich wird der gesamte Vorrat achtmal größer sein. Somit,
500 8 = 4.000 (kg).
Der anfängliche Mehlvorrat im Lager betrug 4.000 kg.
Aus der Betrachtung dieses Problems lässt sich die folgende Regel ableiten.
Um aus einem gegebenen Wert seines Bruchs eine Zahl zu ermitteln, genügt es, diesen Wert durch den Zähler des Bruchs zu dividieren und das Ergebnis mit dem Nenner des Bruchs zu multiplizieren.
Wir haben zwei Probleme beim Finden einer Zahl mit gegebenem Bruch gelöst. Solche Probleme werden, wie aus dem letzten besonders deutlich hervorgeht, durch zwei Aktionen gelöst: Division (wenn ein Teil gefunden wird) und Multiplikation (wenn die ganze Zahl gefunden wird).
Nachdem wir jedoch die Division von Brüchen gelernt haben, können die oben genannten Probleme mit einer Aktion gelöst werden, nämlich: Division durch einen Bruch.
Die letzte Aufgabe kann beispielsweise in einer Aktion wie folgt gelöst werden:
In Zukunft werden wir Probleme lösen, eine Zahl aus ihrem Bruch mit einer Aktion zu finden – der Division.
7. Eine Zahl anhand ihres Prozentsatzes ermitteln.
Bei diesen Aufgaben müssen Sie eine Zahl finden, die einige Prozent dieser Zahl kennt.
Aufgabe 1. Anfang dieses Jahres habe ich 60 Rubel von der Sparkasse erhalten. Einnahmen aus dem Betrag, den ich vor einem Jahr angespart habe. Wie viel Geld habe ich bei der Sparkasse eingezahlt? (Die Kassen geben den Einlegern eine Rendite von 2 % pro Jahr.)
Der Kern des Problems besteht darin, dass ich einen bestimmten Geldbetrag auf eine Sparkasse gelegt habe und dort ein Jahr geblieben bin. Nach einem Jahr erhielt ich 60 Rubel von ihr. Einkommen, das 2/100 des Geldes beträgt, das ich eingezahlt habe. Wie viel Geld habe ich eingezahlt?
Wenn wir also einen Teil dieses Geldes kennen, der auf zwei Arten ausgedrückt wird (in Rubel und Bruchteilen), müssen wir den gesamten, noch unbekannten Betrag ermitteln. Dies ist ein gewöhnliches Problem beim Finden einer Zahl mit gegebenem Bruchteil. Folgende Probleme werden durch Division gelöst:
Das bedeutet, dass 3.000 Rubel bei der Sparkasse eingezahlt wurden.
Aufgabe 2. Die Fischer erfüllten den Monatsplan in zwei Wochen um 64 % und ernteten 512 Tonnen Fisch. Was war ihr Plan?
Aus den Bedingungen des Problems geht hervor, dass die Fischer einen Teil des Plans umgesetzt haben. Dieser Teil entspricht 512 Tonnen, was 64 % des Plans entspricht. Wir wissen nicht, wie viele Tonnen Fisch laut Plan zubereitet werden müssen. Das Finden dieser Nummer wird die Lösung des Problems sein.
Solche Probleme werden durch Division gelöst:
Das bedeutet, dass laut Plan 800 Tonnen Fisch zubereitet werden müssen.
Aufgabe 3. Der Zug fuhr von Riga nach Moskau. Als er den 276. Kilometer hinter sich hatte, fragte einer der Passagiere einen vorbeikommenden Schaffner, wie viel von der Strecke sie bereits zurückgelegt hätten. Darauf antwortete der Schaffner: „Wir haben bereits 30 % der gesamten Fahrt zurückgelegt.“ Wie weit ist es von Riga nach Moskau?
Aus den Problembedingungen geht hervor, dass 30 % der Strecke von Riga nach Moskau 276 km lang sind. Wir müssen die gesamte Entfernung zwischen diesen Städten ermitteln, d. h. für diesen Teil das Ganze:
§ 91. Reziproke Zahlen. Division durch Multiplikation ersetzen.
Nehmen wir den Bruch 2/3 und ersetzen wir den Zähler durch den Nenner, wir erhalten 3/2. Wir haben die Umkehrung dieses Bruchs erhalten.
Um einen Bruch zu erhalten, der die Umkehrung eines bestimmten Bruchs ist, müssen Sie seinen Zähler anstelle des Nenners und den Nenner anstelle des Zählers einsetzen. Auf diese Weise können wir den Kehrwert eines beliebigen Bruchs ermitteln. Zum Beispiel:
3/4, umgekehrt 4/3; 5/6, umgekehrt 6/5
Man nennt zwei Brüche, die die Eigenschaft haben, dass der Zähler des ersten der Nenner des zweiten und der Nenner des ersten der Zähler des zweiten ist gegenseitig umgekehrt.
Lassen Sie uns nun darüber nachdenken, welcher Bruch der Kehrwert von 1/2 sein wird. Offensichtlich wird es 2 / 1 sein, oder einfach 2. Indem wir nach dem Umkehrbruch der gegebenen Eins suchen, erhalten wir eine ganze Zahl. Und dieser Fall ist kein Einzelfall; im Gegenteil, für alle Brüche mit einem Zähler von 1 (eins) sind die Kehrwerte ganze Zahlen, zum Beispiel:
1/3, rückwärts 3; 1/5, umgekehrt 5
Da wir bei der Suche nach Kehrbrüchen auch auf ganze Zahlen gestoßen sind, werden wir im Folgenden nicht von Kehrbrüchen, sondern von Kehrzahlen sprechen.
Lassen Sie uns herausfinden, wie man die Umkehrung einer ganzen Zahl schreibt. Bei Brüchen kann dies einfach gelöst werden: Sie müssen den Nenner anstelle des Zählers einsetzen. Auf die gleiche Weise können Sie die Umkehrung einer ganzen Zahl erhalten, da jede ganze Zahl einen Nenner von 1 haben kann. Das bedeutet, dass die Umkehrung von 7 1/7 sein wird, weil 7 = 7/1; für die Zahl 10 ist die Umkehrung 1/10, da 10 = 10/1
Diese Idee kann anders ausgedrückt werden: Den Kehrwert einer gegebenen Zahl erhält man, indem man eins durch eine gegebene Zahl dividiert. Diese Aussage gilt nicht nur für ganze Zahlen, sondern auch für Brüche. Wenn wir tatsächlich die Umkehrung des Bruchs 5/9 schreiben müssen, können wir 1 nehmen und durch 5/9 dividieren, d. h.

Lassen Sie uns nun auf eines hinweisen Eigentum reziproke Zahlen, die für uns nützlich sein werden: Das Produkt der reziproken Zahlen ist gleich eins. Tatsächlich:
Mithilfe dieser Eigenschaft können wir auf folgende Weise reziproke Zahlen ermitteln. Nehmen wir an, wir müssen die Umkehrung von 8 finden.
Bezeichnen wir es mit dem Buchstaben X , dann 8 X = 1, also X = 1/8. Suchen wir eine andere Zahl, die die Umkehrung von 7/12 ist, und bezeichnen sie mit dem Buchstaben X , dann 7/12 X = 1, also X = 1: 7 / 12 oder X = 12 / 7 .
Wir haben hier das Konzept der reziproken Zahlen eingeführt, um die Informationen zum Teilen von Brüchen etwas zu ergänzen.
Wenn wir die Zahl 6 durch 3/5 teilen, machen wir Folgendes:
![]()
Bitte zahlen Sie Besondere Aufmerksamkeit zum Ausdruck und vergleiche ihn mit dem angegebenen: .
Wenn wir den Ausdruck separat nehmen, ohne Verbindung zum vorherigen, ist es unmöglich, die Frage zu lösen, woher er kommt: aus der Division von 6 durch 3/5 oder aus der Multiplikation von 6 mit 5/3. In beiden Fällen passiert das Gleiche. Deshalb können wir sagen dass die Division einer Zahl durch eine andere durch Multiplikation des Dividenden mit dem Kehrwert des Divisors ersetzt werden kann.
Die unten aufgeführten Beispiele bestätigen diese Schlussfolgerung voll und ganz.
Eine ganze Zahl mit einem Bruch zu multiplizieren ist keine schwierige Aufgabe. Aber es gibt Feinheiten, die Sie wahrscheinlich in der Schule verstanden, aber inzwischen vergessen haben.
Wie man eine ganze Zahl mit einem Bruch multipliziert – ein paar Begriffe
Wenn Sie sich daran erinnern, was ein Zähler und ein Nenner sind und wie sich ein echter Bruch von einem unechten Bruch unterscheidet, überspringen Sie diesen Absatz. Es ist für diejenigen, die die Theorie völlig vergessen haben.
Der Zähler ist der obere Teil des Bruchs – was wir dividieren. Der Nenner ist kleiner. Das ist es, wonach wir dividieren.
Ein echter Bruch ist ein Bruch, dessen Zähler kleiner als sein Nenner ist. Ein unechter Bruch ist ein Bruch, dessen Zähler größer oder gleich seinem Nenner ist.
So multiplizieren Sie eine ganze Zahl mit einem Bruch
Die Regel zum Multiplizieren einer ganzen Zahl mit einem Bruch ist sehr einfach: Wir multiplizieren den Zähler mit der ganzen Zahl, berühren aber nicht den Nenner. Zum Beispiel: zwei multipliziert mit einem Fünftel – wir erhalten zwei Fünftel. Vier multipliziert mit drei Sechzehnteln ergibt zwölf Sechzehntel.


Die Ermäßigung
Im zweiten Beispiel kann der resultierende Bruch reduziert werden.
Was bedeutet das? Bitte beachten Sie, dass sowohl der Zähler als auch der Nenner dieses Bruchs durch vier teilbar sind. Die Division beider Zahlen durch einen gemeinsamen Teiler nennt man Bruchreduzierung. Wir bekommen drei Viertel.


Unechte Brüche
Aber nehmen wir an, wir multiplizieren vier mit zwei Fünfteln. Es stellte sich heraus, dass es acht Fünftel waren. Dies ist ein unechter Bruch.
Es muss unbedingt in die richtige Form gebracht werden. Dazu müssen Sie ein ganzes Teil daraus auswählen.
Hier müssen Sie eine Division mit Rest verwenden. Als Rest erhalten wir eins und drei.
Ein ganzes und drei Fünftel ist unser echter Bruchteil.
Etwas schwieriger ist es, fünfunddreißig Achtel in die richtige Form zu bringen. Die Zahl, die der Zahl siebenunddreißig am nächsten kommt und durch acht teilbar ist, ist zweiunddreißig. Bei der Teilung erhalten wir vier. Subtrahieren Sie zweiunddreißig von fünfunddreißig, erhalten Sie drei. Ergebnis: vier ganze und drei Achtel.


Gleichheit von Zähler und Nenner. Und hier ist alles sehr einfach und schön. Wenn Zähler und Nenner gleich sind, ist das Ergebnis einfach eins.
Wir werden die Multiplikation gewöhnlicher Brüche in mehreren möglichen Varianten betrachten.
Einen gewöhnlichen Bruch mit einem Bruch multiplizieren
Dies ist der einfachste Fall, in dem Sie Folgendes verwenden müssen Regeln für die Multiplikation von Brüchen.
Zu Bruch mit Bruch multiplizieren, notwendig:
- Multiplizieren Sie den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs und schreiben Sie ihr Produkt in den Zähler des neuen Bruchs.
- Multiplizieren Sie den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs und schreiben Sie ihr Produkt in den Nenner des neuen Bruchs.
- Brüche mit gleichem Nenner addieren
- Brüche mit unterschiedlichen Nennern addieren
Bevor Sie Zähler und Nenner multiplizieren, prüfen Sie, ob sich die Brüche reduzieren lassen. Durch die Reduzierung von Brüchen in Berechnungen werden Ihre Berechnungen erheblich einfacher.

Einen Bruch mit einer natürlichen Zahl multiplizieren
Einen Bruch machen mit einer natürlichen Zahl multiplizieren Sie müssen den Zähler des Bruchs mit dieser Zahl multiplizieren und den Nenner des Bruchs unverändert lassen.
Wenn das Ergebnis der Multiplikation ein unechter Bruch ist, vergessen Sie nicht, ihn in eine gemischte Zahl umzuwandeln, d. h. den ganzen Teil hervorzuheben.

Gemischte Zahlen multiplizieren
Um gemischte Zahlen zu multiplizieren, müssen Sie sie zunächst in unechte Brüche umwandeln und dann gemäß der Regel zur Multiplikation gewöhnlicher Brüche multiplizieren.

Eine andere Möglichkeit, einen Bruch mit einer natürlichen Zahl zu multiplizieren
Manchmal ist es bei Berechnungen bequemer, eine andere Multiplikationsmethode zu verwenden gemeinsamer Bruch pro Nummer.
Um einen Bruch mit einer natürlichen Zahl zu multiplizieren, müssen Sie den Nenner des Bruchs durch diese Zahl dividieren und den Zähler gleich lassen.

Wie aus dem Beispiel hervorgeht, ist diese Version der Regel bequemer anzuwenden, wenn der Nenner des Bruchs ohne Rest durch eine natürliche Zahl teilbar ist.
Operationen mit Brüchen
Brüche mit gleichem Nenner addieren
Es gibt zwei Arten der Addition von Brüchen:
Lassen Sie uns zunächst die Addition von Brüchen mit gleichen Nennern lernen. Hier ist alles einfach. Um Brüche mit demselben Nenner zu addieren, müssen Sie deren Zähler addieren und den Nenner unverändert lassen. Addieren wir zum Beispiel die Brüche und . Addieren Sie die Zähler und lassen Sie den Nenner unverändert:

Dieses Beispiel lässt sich leicht verstehen, wenn wir uns an die Pizza erinnern, die in vier Teile geteilt ist. Wenn man Pizza zu Pizza hinzufügt, erhält man Pizza:
Beispiel 2. Addiere Brüche und .
Auch hier addieren wir die Zähler und lassen den Nenner unverändert:

Es stellte sich heraus, dass die Antwort ein unechter Bruch war. Am Ende der Aufgabe ist es üblich, unechte Brüche loszuwerden. Um einen unechten Bruch loszuwerden, müssen Sie den ganzen Teil davon auswählen. In unserem Fall lässt sich der ganze Teil leicht isolieren – zwei geteilt durch zwei ergibt eins:

Dieses Beispiel lässt sich leicht verstehen, wenn wir uns an eine Pizza erinnern, die in zwei Teile geteilt ist. Wenn man der Pizza noch mehr Pizza hinzufügt, erhält man eine ganze Pizza:
Beispiel 3. Addiere Brüche und .
![]()
Dieses Beispiel lässt sich leicht verstehen, wenn wir uns an die Pizza erinnern, die in drei Teile geteilt ist. Wenn man der Pizza noch mehr Pizza hinzufügt, erhält man Pizza:
Beispiel 4. Finden Sie den Wert eines Ausdrucks 
Dieses Beispiel wird genauso gelöst wie die vorherigen. Die Zähler müssen addiert und der Nenner unverändert gelassen werden:
Versuchen wir, unsere Lösung anhand einer Zeichnung darzustellen. Wenn Sie einer Pizza Pizzen hinzufügen und weitere Pizzen hinzufügen, erhalten Sie 1 ganze Pizza und weitere Pizzen.
Wie Sie sehen, ist das Addieren von Brüchen mit demselben Nenner nicht kompliziert. Es reicht aus, die folgenden Regeln zu verstehen:
- Um Brüche mit demselben Nenner zu addieren, müssen Sie deren Zähler addieren und den Nenner gleich lassen;
- Wenn sich herausstellt, dass die Antwort ein unechter Bruch ist, müssen Sie den gesamten Teil davon hervorheben.
- Finden Sie den LCM der Nenner von Brüchen.
- Teilen Sie den LCM durch den Nenner jedes Bruchs und erhalten Sie einen zusätzlichen Faktor für jeden Bruch.
- Multiplizieren Sie die Zähler und Nenner von Brüchen mit ihren zusätzlichen Faktoren;
- Addiere Brüche, die den gleichen Nenner haben;
- Wenn sich herausstellt, dass die Antwort ein unechter Bruch ist, wählen Sie seinen ganzen Teil aus.
- Brüche mit gleichem Nenner subtrahieren
- Brüche mit unterschiedlichen Nennern subtrahieren
Brüche mit unterschiedlichen Nennern addieren
Jetzt lernen wir, wie man Brüche mit unterschiedlichen Nennern addiert. Beim Addieren von Brüchen müssen die Nenner der Brüche gleich sein. Aber sie sind nicht immer gleich.
Brüche können beispielsweise addiert werden, weil sie den gleichen Nenner haben.
Aber Brüche können nicht sofort addiert werden, da diese Brüche verschiedene Nenner. In solchen Fällen müssen Brüche auf den gleichen (gemeinsamen) Nenner reduziert werden.
Es gibt mehrere Möglichkeiten, Brüche auf denselben Nenner zu reduzieren. Heute werden wir uns nur eine davon ansehen, da die anderen Methoden für einen Anfänger möglicherweise kompliziert erscheinen.
Der Kern dieser Methode besteht darin, dass wir zunächst nach dem kleinsten gemeinsamen Vielfachen (LCM) der Nenner beider Brüche suchen. Der LCM wird dann durch den Nenner des ersten Bruchs dividiert, um den ersten zusätzlichen Faktor zu erhalten. Das Gleiche machen sie mit dem zweiten Bruch – der LCM wird durch den Nenner des zweiten Bruchs dividiert und man erhält einen zweiten zusätzlichen Faktor.
Anschließend werden Zähler und Nenner der Brüche mit ihren zusätzlichen Faktoren multipliziert. Als Ergebnis dieser Aktionen werden Brüche mit unterschiedlichen Nennern zu Brüchen mit demselben Nenner. Und wir wissen bereits, wie man solche Brüche addiert.
Beispiel 1. Addieren wir die Brüche und
Diese Brüche haben unterschiedliche Nenner, daher müssen Sie sie auf denselben (gemeinsamen) Nenner reduzieren.
Zunächst ermitteln wir das kleinste gemeinsame Vielfache der Nenner beider Brüche. Der Nenner des ersten Bruchs ist die Zahl 3 und der Nenner des zweiten Bruchs ist die Zahl 2. Das kleinste gemeinsame Vielfache dieser Zahlen ist 6
LCM (2 und 3) = 6
Kommen wir nun zurück zu den Brüchen und . Teilen Sie zunächst den LCM durch den Nenner des ersten Bruchs und erhalten Sie den ersten zusätzlichen Faktor. LCM ist die Zahl 6 und der Nenner des ersten Bruchs ist die Zahl 3. Teilen Sie 6 durch 3, wir erhalten 2.
Die resultierende Zahl 2 ist der erste zusätzliche Multiplikator. Wir schreiben es bis zum ersten Bruch auf. Machen Sie dazu einen kleinen schrägen Strich über den Bruch und notieren Sie den darüber liegenden Zusatzfaktor:
Dasselbe machen wir mit dem zweiten Bruch. Wir dividieren den LCM durch den Nenner des zweiten Bruchs und erhalten den zweiten zusätzlichen Faktor. LCM ist die Zahl 6 und der Nenner des zweiten Bruchs ist die Zahl 2. Teilen Sie 6 durch 2, wir erhalten 3.
Die resultierende Zahl 3 ist der zweite zusätzliche Multiplikator. Wir schreiben es bis zum zweiten Bruch auf. Wieder machen wir einen kleinen schrägen Strich über den zweiten Bruch und notieren den darüber liegenden zusätzlichen Faktor:
Jetzt haben wir alles zum Hinzufügen bereit. Es bleibt noch, die Zähler und Nenner der Brüche mit ihren zusätzlichen Faktoren zu multiplizieren:

Schauen Sie sich genau an, wozu wir gekommen sind. Wir kamen zu dem Schluss, dass Brüche mit unterschiedlichen Nennern zu Brüchen mit gleichen Nennern wurden. Und wir wissen bereits, wie man solche Brüche addiert. Lassen Sie uns dieses Beispiel bis zum Ende durchgehen:

Damit ist das Beispiel abgeschlossen. Es stellt sich heraus, hinzuzufügen.
Versuchen wir, unsere Lösung anhand einer Zeichnung darzustellen. Wenn man einer Pizza Pizza hinzufügt, erhält man eine ganze Pizza und ein weiteres Sechstel einer Pizza:
Auch das Zusammenführen von Brüchen auf den gleichen (gemeinsamen) Nenner kann mit einem Bild dargestellt werden. Indem wir die Brüche und auf einen gemeinsamen Nenner reduzieren, erhalten wir die Brüche und . Diese beiden Brüche werden durch die gleichen Pizzastücke repräsentiert. Der einzige Unterschied besteht darin, dass sie diesmal in gleiche Anteile aufgeteilt (auf den gleichen Nenner reduziert) werden.

Die erste Zeichnung stellt einen Bruch dar (vier von sechs Teilen), und die zweite Zeichnung stellt einen Bruch dar (drei von sechs Teilen). Wenn wir diese Teile addieren, erhalten wir (sieben von sechs Teilen). Dieser Bruch ist unechten, daher haben wir den gesamten Teil hervorgehoben. Als Ergebnis bekamen wir (eine ganze Pizza und eine weitere sechste Pizza).
Bitte beachten Sie, was wir beschrieben haben dieses Beispiel zu detailliert. IN Bildungsinstitutionen Es ist nicht üblich, so ausführlich zu schreiben. Sie müssen in der Lage sein, schnell den LCM beider Nenner und zusätzlicher Faktoren zu finden und die gefundenen zusätzlichen Faktoren schnell mit Ihren Zählern und Nennern zu multiplizieren. Wenn wir in der Schule wären, müssten wir dieses Beispiel wie folgt schreiben:

Aber es gibt auch eine andere Seite der Medaille. Wenn man sich in den ersten Phasen des Mathematikstudiums keine detaillierten Notizen macht, tauchen solche Fragen auf. „Woher kommt diese Zahl?“, „Warum werden Brüche plötzlich zu ganz anderen Brüchen?“ «.
Um das Addieren von Brüchen mit unterschiedlichen Nennern zu erleichtern, können Sie die folgende Schritt-für-Schritt-Anleitung verwenden:
Beispiel 2. Finden Sie den Wert eines Ausdrucks  .
.
Verwenden wir das oben bereitgestellte Diagramm.
Schritt 1. Finden Sie den LCM für die Nenner der Brüche
Finden Sie den LCM für die Nenner beider Brüche. Die Nenner der Brüche sind die Zahlen 2, 3 und 4. Sie müssen den LCM für diese Zahlen ermitteln:
Schritt 2. Teilen Sie den LCM durch den Nenner jedes Bruchs und erhalten Sie einen zusätzlichen Faktor für jeden Bruch
Teilen Sie den LCM durch den Nenner des ersten Bruchs. LCM ist die Zahl 12 und der Nenner des ersten Bruchs ist die Zahl 2. Teilen Sie 12 durch 2, wir erhalten 6. Wir erhalten den ersten zusätzlichen Faktor 6. Wir schreiben ihn über den ersten Bruch:
Nun dividieren wir den LCM durch den Nenner des zweiten Bruchs. LCM ist die Zahl 12 und der Nenner des zweiten Bruchs ist die Zahl 3. Teilen Sie 12 durch 3, wir erhalten 4. Wir erhalten den zweiten zusätzlichen Faktor 4. Wir schreiben ihn über den zweiten Bruch:
Nun dividieren wir den LCM durch den Nenner des dritten Bruchs. LCM ist die Zahl 12 und der Nenner des dritten Bruchs ist die Zahl 4. Teilen Sie 12 durch 4, wir erhalten 3. Wir erhalten den dritten zusätzlichen Faktor 3. Wir schreiben ihn über den dritten Bruch:
Schritt 3. Multiplizieren Sie die Zähler und Nenner der Brüche mit ihren zusätzlichen Faktoren
Wir multiplizieren die Zähler und Nenner mit ihren zusätzlichen Faktoren:
Schritt 4. Addiere Brüche mit demselben Nenner
Wir kamen zu dem Schluss, dass Brüche mit unterschiedlichen Nennern zu Brüchen mit demselben (gemeinsamen) Nenner wurden. Jetzt müssen nur noch diese Brüche addiert werden. Addiere es zusammen:

Der Zusatz passte nicht in eine Zeile, daher haben wir den verbleibenden Ausdruck in die nächste Zeile verschoben. Das ist in der Mathematik erlaubt. Wenn ein Ausdruck nicht in eine Zeile passt, wird er in die nächste Zeile verschoben, und am Ende der ersten Zeile und am Anfang der neuen Zeile muss ein Gleichheitszeichen (=) eingefügt werden. Das Gleichheitszeichen in der zweiten Zeile zeigt an, dass es sich um eine Fortsetzung des Ausdrucks aus der ersten Zeile handelt.
Schritt 5. Wenn sich herausstellt, dass die Antwort ein unechter Bruch ist, markieren Sie seinen gesamten Teil
Es stellte sich heraus, dass unsere Antwort ein unechter Bruch war. Wir müssen einen ganzen Teil davon hervorheben. Wir heben hervor:

Wir haben eine Antwort erhalten
Brüche mit gleichem Nenner subtrahieren
Es gibt zwei Arten der Subtraktion von Brüchen:
Lassen Sie uns zunächst lernen, wie man Brüche mit gleichen Nennern subtrahiert. Hier ist alles einfach. Um einen anderen von einem Bruch zu subtrahieren, müssen Sie den Zähler des zweiten Bruchs vom Zähler des ersten Bruchs subtrahieren, den Nenner jedoch gleich lassen.
Lassen Sie uns zum Beispiel den Wert des Ausdrucks ermitteln. Um dieses Beispiel zu lösen, müssen Sie den Zähler des zweiten Bruchs vom Zähler des ersten Bruchs subtrahieren und den Nenner gleich lassen. Lass uns das machen:

Dieses Beispiel lässt sich leicht verstehen, wenn wir uns an die Pizza erinnern, die in vier Teile geteilt ist. Wenn man aus einer Pizza Pizzen schneidet, erhält man Pizzen:
Beispiel 2. Finden Sie den Wert des Ausdrucks.
Subtrahieren Sie erneut vom Zähler des ersten Bruchs den Zähler des zweiten Bruchs und lassen Sie den Nenner gleich:

Dieses Beispiel lässt sich leicht verstehen, wenn wir uns an die Pizza erinnern, die in drei Teile geteilt ist. Wenn man aus einer Pizza Pizzen schneidet, erhält man Pizzen:
Beispiel 3. Finden Sie den Wert eines Ausdrucks 
Dieses Beispiel wird genauso gelöst wie die vorherigen. Vom Zähler des ersten Bruchs müssen Sie die Zähler der übrigen Brüche subtrahieren:

Die Antwort war ein unechter Bruch. Wenn das Beispiel abgeschlossen ist, ist es üblich, den unechten Bruch zu entfernen. Lassen Sie uns den unechten Bruch in der Antwort loswerden. Wählen wir dazu den gesamten Teil aus:
Wie Sie sehen, ist das Subtrahieren von Brüchen mit demselben Nenner nichts Kompliziertes. Es reicht aus, die folgenden Regeln zu verstehen:
Brüche mit unterschiedlichen Nennern subtrahieren
Sie können beispielsweise einen Bruch von einem Bruch subtrahieren, weil die Brüche den gleichen Nenner haben. Sie können jedoch keinen Bruch von einem Bruch subtrahieren, da diese Brüche unterschiedliche Nenner haben. In solchen Fällen müssen Brüche auf den gleichen (gemeinsamen) Nenner reduziert werden.
Der gemeinsame Nenner wird nach dem gleichen Prinzip ermittelt, das wir bei der Addition von Brüchen mit unterschiedlichen Nennern verwendet haben. Ermitteln Sie zunächst den LCM der Nenner beider Brüche. Dann wird der LCM durch den Nenner des ersten Bruchs dividiert und man erhält den ersten zusätzlichen Faktor, der über dem ersten Bruch geschrieben wird. Ebenso wird der LCM durch den Nenner des zweiten Bruchs dividiert und man erhält einen zweiten zusätzlichen Faktor, der über dem zweiten Bruch geschrieben wird.
Die Brüche werden dann mit ihren zusätzlichen Faktoren multipliziert. Als Ergebnis dieser Operationen werden Brüche mit unterschiedlichen Nennern in Brüche mit gleichen Nennern umgewandelt. Und wir wissen bereits, wie man solche Brüche subtrahiert.
Beispiel 1. Finden Sie die Bedeutung des Ausdrucks:
Zuerst ermitteln wir den LCM der Nenner beider Brüche. Der Nenner des ersten Bruchs ist die Zahl 3 und der Nenner des zweiten Bruchs ist die Zahl 4. Das kleinste gemeinsame Vielfache dieser Zahlen ist 12
LCM (3 und 4) = 12
Kommen wir nun zurück zu den Brüchen und
Suchen wir einen zusätzlichen Faktor für den ersten Bruch. Teilen Sie dazu den LCM durch den Nenner des ersten Bruchs. LCM ist die Zahl 12 und der Nenner des ersten Bruchs ist die Zahl 3. Teilen Sie 12 durch 3, wir erhalten 4. Schreiben Sie eine Vier über den ersten Bruch:
Dasselbe machen wir mit dem zweiten Bruch. Teilen Sie den LCM durch den Nenner des zweiten Bruchs. LCM ist die Zahl 12 und der Nenner des zweiten Bruchs ist die Zahl 4. Teilen Sie 12 durch 4, wir erhalten 3. Schreiben Sie eine Drei über den zweiten Bruch:
Jetzt sind wir bereit für die Subtraktion. Es bleibt noch, die Brüche mit ihren zusätzlichen Faktoren zu multiplizieren:

Wir kamen zu dem Schluss, dass Brüche mit unterschiedlichen Nennern zu Brüchen mit gleichen Nennern wurden. Und wir wissen bereits, wie man solche Brüche subtrahiert. Lassen Sie uns dieses Beispiel bis zum Ende durchgehen:

Wir haben eine Antwort erhalten
Versuchen wir, unsere Lösung anhand einer Zeichnung darzustellen. Wenn man aus einer Pizza Pizza schneidet, erhält man Pizza
Dies ist die detaillierte Version der Lösung. Wenn wir in der Schule wären, müssten wir dieses Beispiel kürzer lösen. Eine solche Lösung würde so aussehen:

Auch das Zusammenführen von Brüchen auf einen gemeinsamen Nenner lässt sich anhand eines Bildes veranschaulichen. Wenn wir diese Brüche auf einen gemeinsamen Nenner bringen, erhalten wir die Brüche und . Diese Brüche werden durch die gleichen Pizzastücke dargestellt, dieses Mal werden sie jedoch in gleiche Anteile aufgeteilt (auf den gleichen Nenner reduziert):

Das erste Bild zeigt einen Bruch (acht von zwölf Stücken), und das zweite Bild zeigt einen Bruch (drei von zwölf Stücken). Indem wir aus acht Stücken drei Stücke schneiden, erhalten wir fünf aus zwölf Stücken. Der Bruch beschreibt diese fünf Teile.
Beispiel 2. Finden Sie den Wert eines Ausdrucks 
Diese Brüche haben unterschiedliche Nenner, daher müssen Sie sie zunächst auf denselben (gemeinsamen) Nenner reduzieren.
Lassen Sie uns den LCM der Nenner dieser Brüche ermitteln.
Die Nenner der Brüche sind die Zahlen 10, 3 und 5. Das kleinste gemeinsame Vielfache dieser Zahlen ist 30
LCM(10, 3, 5) = 30
Jetzt finden wir für jeden Bruch zusätzliche Faktoren. Teilen Sie dazu den LCM durch den Nenner jedes Bruchs.
Suchen wir einen zusätzlichen Faktor für den ersten Bruch. LCM ist die Zahl 30 und der Nenner des ersten Bruchs ist die Zahl 10. Teilen Sie 30 durch 10, wir erhalten den ersten zusätzlichen Faktor 3. Wir schreiben ihn über den ersten Bruch:
Nun finden wir einen zusätzlichen Faktor für den zweiten Bruch. Teilen Sie den LCM durch den Nenner des zweiten Bruchs. LCM ist die Zahl 30 und der Nenner des zweiten Bruchs ist die Zahl 3. Teilen Sie 30 durch 3, wir erhalten den zweiten zusätzlichen Faktor 10. Wir schreiben ihn über den zweiten Bruch:
Nun finden wir einen zusätzlichen Faktor für den dritten Bruch. Teilen Sie den LCM durch den Nenner des dritten Bruchs. LCM ist die Zahl 30 und der Nenner des dritten Bruchs ist die Zahl 5. Teilen Sie 30 durch 5, wir erhalten den dritten zusätzlichen Faktor 6. Wir schreiben ihn über den dritten Bruch:
Jetzt ist alles zur Subtraktion bereit. Es bleibt noch, die Brüche mit ihren zusätzlichen Faktoren zu multiplizieren:
Wir kamen zu dem Schluss, dass Brüche mit unterschiedlichen Nennern zu Brüchen mit demselben (gemeinsamen) Nenner wurden. Und wir wissen bereits, wie man solche Brüche subtrahiert. Lassen Sie uns dieses Beispiel beenden.
Die Fortsetzung des Beispiels passt nicht in eine Zeile, daher verschieben wir die Fortsetzung in die nächste Zeile. Vergessen Sie nicht das Gleichheitszeichen (=) in der neuen Zeile:

Es stellte sich heraus, dass die Antwort ein regulärer Bruch war, und alles scheint zu uns zu passen, aber es ist zu umständlich und hässlich. Es wäre notwendig, es einfacher und ästhetisch ansprechender zu machen. Was kann getan werden? Sie können diesen Bruch kürzen. Denken Sie daran, dass die Reduzierung eines Bruchs die Division von Zähler und Nenner durch den größten gemeinsamen Teiler von Zähler und Nenner ist.
Um einen Bruch korrekt zu reduzieren, müssen Sie seinen Zähler und Nenner durch den größten gemeinsamen Teiler (GCD) der Zahlen 20 und 30 dividieren.
GCD sollte nicht mit NOC verwechselt werden. Der häufigste Fehler vieler Anfänger. GCD ist der größte gemeinsame Teiler. Wir finden es, um einen Bruch zu reduzieren.
Und LCM ist das kleinste gemeinsame Vielfache. Wir finden es, um Brüche auf den gleichen (gemeinsamen) Nenner zu bringen.
Jetzt ermitteln wir den größten gemeinsamen Teiler (GCD) der Zahlen 20 und 30.
Also finden wir GCD für die Nummern 20 und 30:
GCD (20 und 30) = 10
Nun kehren wir zu unserem Beispiel zurück und dividieren Zähler und Nenner des Bruchs durch 10:

Wir haben eine schöne Antwort erhalten
Einen Bruch mit einer Zahl multiplizieren
Um einen Bruch mit einer Zahl zu multiplizieren, müssen Sie den Zähler des gegebenen Bruchs mit dieser Zahl multiplizieren und den Nenner gleich lassen.
Beispiel 1. Multiplizieren Sie einen Bruch mit der Zahl 1.
Multiplizieren Sie den Zähler des Bruchs mit der Zahl 1
![]()
Die Aufnahme kann als Halbzeitaufnahme verstanden werden. Wer zum Beispiel einmal Pizza isst, bekommt Pizza

Aus den Gesetzen der Multiplikation wissen wir, dass sich das Produkt nicht ändert, wenn der Multiplikand und der Faktor vertauscht werden. Wenn der Ausdruck als geschrieben wird, ist das Produkt immer noch gleich. Auch hier gilt die Regel zum Multiplizieren einer ganzen Zahl und eines Bruchs:
![]()
Diese Notation kann so verstanden werden, dass sie die Hälfte von eins nimmt. Wenn es zum Beispiel eine ganze Pizza gibt und wir die Hälfte davon nehmen, dann haben wir Pizza:

Beispiel 2. Finden Sie den Wert eines Ausdrucks
Multiplizieren Sie den Zähler des Bruchs mit 4
![]()
![]()
Der Ausdruck kann so verstanden werden, dass er zwei Viertel viermal einnimmt. Wenn Sie beispielsweise 4 Pizzen nehmen, erhalten Sie zwei ganze Pizzen

Und wenn wir den Multiplikanden und den Multiplikator vertauschen, erhalten wir den Ausdruck. Es wird auch gleich 2 sein. Dieser Ausdruck kann so verstanden werden, dass man aus vier ganzen Pizzen zwei Pizzen nimmt:

Brüche multiplizieren
Um Brüche zu multiplizieren, müssen Sie deren Zähler und Nenner multiplizieren. Wenn sich herausstellt, dass die Antwort ein unechter Bruch ist, müssen Sie den ganzen Teil davon hervorheben.
Beispiel 1. Finden Sie den Wert des Ausdrucks.
![]()
Wir haben eine Antwort erhalten. Es empfiehlt sich, diesen Anteil zu reduzieren. Der Bruch kann um 2 reduziert werden. Dann wird die endgültige Lösung die folgende Form annehmen:

Der Ausdruck kann so verstanden werden, dass man aus einer halben Pizza eine Pizza nimmt. Nehmen wir an, wir haben eine halbe Pizza:
Wie nimmt man aus dieser Hälfte zwei Drittel? Zuerst müssen Sie diese Hälfte in drei gleiche Teile teilen:

Und nimm zwei von diesen drei Teilen:

Wir machen Pizza. Denken Sie daran, wie Pizza aussieht, wenn sie in drei Teile geteilt wird:

Ein Stück dieser Pizza und die beiden Stücke, die wir genommen haben, werden die gleichen Abmessungen haben:

Mit anderen Worten, es handelt sich um eine Pizza gleicher Größe. Daher ist der Wert des Ausdrucks

Beispiel 2. Finden Sie den Wert eines Ausdrucks
Multiplizieren Sie den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs und den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs:

Die Antwort war ein unechter Bruch. Lassen Sie uns den gesamten Teil davon hervorheben:
![]()
Beispiel 3. Finden Sie den Wert eines Ausdrucks
![]()
Es stellte sich heraus, dass die Antwort ein regulärer Bruch war, aber es wäre gut, wenn er gekürzt würde. Um diesen Bruch zu reduzieren, muss er durch den ggT von Zähler und Nenner dividiert werden. Lassen Sie uns also den gcd der Zahlen 105 und 450 ermitteln:
Der GCD für (105 und 150) beträgt 15
Jetzt dividieren wir Zähler und Nenner unserer Antwort durch ggT:
Darstellung einer ganzen Zahl als Bruch
Jede ganze Zahl kann als Bruch dargestellt werden. Beispielsweise kann die Zahl 5 als dargestellt werden. Dies ändert nichts an der Bedeutung von fünf, da der Ausdruck „die Zahl fünf geteilt durch eins“ bedeutet und dies, wie wir wissen, gleich fünf ist:
Reziproke Zahlen
Jetzt werden wir uns sehr kennenlernen interessantes Thema in Mathematik. Es heißt „umgekehrte Zahlen“.
Definition. Umgekehrt zur Nummer A ist eine Zahl, die multipliziert mit A gibt einen.
Ersetzen wir in dieser Definition die Variable A Nummer 5 und versuchen Sie, die Definition zu lesen:
Umgekehrt zur Nummer 5 ist eine Zahl, die multipliziert mit 5 gibt einen.
Ist es möglich, eine Zahl zu finden, die, wenn man sie mit 5 multipliziert, eins ergibt? Es stellt sich heraus, dass es möglich ist. Stellen wir uns fünf als Bruch vor:
Dann multiplizieren Sie diesen Bruch mit sich selbst, indem Sie einfach Zähler und Nenner vertauschen. Mit anderen Worten: Multiplizieren Sie einen Bruch mit sich selbst, nur umgekehrt:
Was wird dadurch passieren? Wenn wir dieses Beispiel weiter lösen, erhalten wir eines:
![]()
Das bedeutet, dass die Umkehrung der Zahl 5 die Zahl ist, denn wenn man 5 mit multipliziert, erhält man eins.
Der Kehrwert einer Zahl kann auch für jede andere ganze Zahl ermittelt werden.
- Der Kehrwert von 3 ist ein Bruch
- Der Kehrwert von 4 ist ein Bruch
Sie können auch den Kehrwert jedes anderen Bruchs ermitteln. Drehen Sie es dazu einfach um.
KOMMEN SIE SCHON ÜBER DIESE RECHEN AB! 🙂
Brüche multiplizieren und dividieren.
Aufmerksamkeit!
Es gibt noch weitere
Materialien im Sonderabschnitt 555.
Für diejenigen, die sehr „nicht sehr“ sind. »
Und für diejenigen, die „sehr sehr.“ ")
Diese Operation ist viel angenehmer als Addition und Subtraktion! Weil es einfacher ist. Zur Erinnerung: Um einen Bruch mit einem Bruch zu multiplizieren, müssen Sie die Zähler (dies ist der Zähler des Ergebnisses) und die Nenner (dies ist der Nenner) multiplizieren. Also:


Alles ist extrem einfach. Und bitte nicht nach einem gemeinsamen Nenner suchen! Hier ist er nicht nötig...
Um einen Bruch durch einen Bruch zu dividieren, müssen Sie umkehren zweite(Das ist wichtig!) Brüche und multipliziere sie, d. h.:


Wenn Sie auf Multiplikation oder Division mit ganzen Zahlen und Brüchen stoßen, ist das in Ordnung. Wie bei der Addition bilden wir aus einer ganzen Zahl mit Eins im Nenner einen Bruch – und machen Sie weiter! Zum Beispiel:

In der Oberstufe muss man sich oft mit dreistöckigen (oder sogar vierstöckigen!) Brüchen auseinandersetzen. Zum Beispiel:
Wie kann ich diesen Bruch anständig aussehen lassen? Ja, ganz einfach! Verwenden Sie die Zweipunktdivision:

Aber vergessen Sie nicht die Reihenfolge der Teilung! Im Gegensatz zur Multiplikation ist dies hier sehr wichtig! Natürlich werden wir 4:2 oder 2:4 nicht verwechseln. Aber in einem dreistöckigen Bruchteil kann man leicht einen Fehler machen. Bitte beachten Sie zum Beispiel:
Im ersten Fall (Ausdruck links):

Im zweiten (Ausdruck rechts):

Spüren Sie den Unterschied? 4 und 1/9!
Was bestimmt die Reihenfolge der Teilung? Entweder mit Klammern, oder (wie hier) mit der Länge horizontaler Linien. Entwickeln Sie Ihr Auge. Und wenn es keine Klammern oder Bindestriche gibt, wie zum Beispiel:
dann dividieren und multiplizieren der Reihe nach von links nach rechts!
Und auch sehr einfach und wichtige Technik. Bei Aktionen mit Abschlüssen wird es Ihnen sehr nützlich sein! Teilen wir eins durch einen beliebigen Bruch, zum Beispiel durch 13/15:

Der Schuss ist umgekippt! Und das passiert immer. Wenn man 1 durch einen beliebigen Bruch dividiert, ist das Ergebnis derselbe Bruch, nur umgekehrt.
Das ist alles für Operationen mit Brüchen. Die Sache ist ganz einfach, aber es gibt mehr als genug Fehler. Berücksichtigen Sie praktische Ratschläge und es wird weniger (Fehler) geben!
1. Das Wichtigste bei der Arbeit mit gebrochenen Ausdrücken ist Genauigkeit und Aufmerksamkeit! Es ist nicht gebräuchliche Worte, keine guten Wünsche! Das ist eine dringende Notwendigkeit! Führen Sie alle Berechnungen zum Einheitlichen Staatsexamen als vollwertige Aufgabe, konzentriert und klar durch. Es ist besser, zwei zusätzliche Zeilen in Ihren Entwurf zu schreiben, als bei den mentalen Berechnungen Fehler zu machen.
2. In Beispielen mit verschiedene Typen Brüche – Fahren Sie mit gewöhnlichen Brüchen fort.
3. Wir reduzieren alle Brüche bis zum Anschlag.
4. Wir reduzieren mehrstufige Bruchausdrücke auf gewöhnliche Ausdrücke, indem wir die Division durch zwei Punkte verwenden (wir folgen der Divisionsreihenfolge!).
Hier sind die Aufgaben, die Sie unbedingt erledigen müssen. Nach allen Aufgaben werden Antworten gegeben. Nutzen Sie die Materialien zu diesem Thema und praktische Tipps. Schätzen Sie, wie viele Beispiele Sie richtig lösen konnten. Das erste Mal! Ohne Taschenrechner! Und ziehen Sie die richtigen Schlussfolgerungen.
Denken Sie daran – die richtige Antwort lautet ab dem zweiten (besonders dem dritten) Mal erhaltenen Informationen zählen nicht! So ist das harte Leben.
Also, im Prüfungsmodus lösen ! Das ist übrigens schon eine Vorbereitung auf das Einheitliche Staatsexamen. Wir lösen das Beispiel, überprüfen es und lösen das nächste. Wir haben alles entschieden - von Anfang bis Ende noch einmal überprüft. Und nur Dann Schauen Sie sich die Antworten an.


Wir suchen nach Antworten, die zu Ihren passen. Ich habe sie absichtlich unordentlich aufgeschrieben, sozusagen fernab der Versuchung. Hier sind sie, die Antworten, durch Semikolons getrennt.
0; 17/22; 3/4; 2/5; 1; 25.
Jetzt ziehen wir Schlussfolgerungen. Wenn alles geklappt hat, freue ich mich für dich! Einfache Berechnungen mit Brüchen sind nicht Ihr Problem! Sie können ernstere Dinge tun. Wenn nicht.
Sie haben also eines von zwei Problemen. Oder beides gleichzeitig.) Mangelndes Wissen und (oder) Unaufmerksamkeit. Aber. Das lösbar Probleme.
Alle diese (und mehr!) Beispiele werden im Sonderabschnitt 555 „Brüche“ besprochen. Mit ausführlichen Erklärungen zum Was, Warum und Wie. Diese Analyse hilft sehr bei mangelndem Wissen und Können!
Ja, und zum zweiten Problem gibt es da etwas.) Ganz praktische Ratschläge, wie man aufmerksamer wird. Ja Ja! Ratschläge, die angewendet werden können jeden.
Erfolg erfordert neben Wissen und Aufmerksamkeit auch eine gewisse Automatismus. Wo kann ich das bekommen? Ich höre ein schweres Seufzen... Ja, nur in der Praxis, nirgendwo anders.
Für Schulungen können Sie die Website 321start.ru besuchen. Dort gibt es in der Option „Ausprobieren“ 10 Beispiele für jeden. Mit sofortiger Verifizierung. Für registrierte Benutzer - 34 Beispiele von einfach bis schwer. Dies geschieht nur in Bruchteilen.
Wenn Ihnen diese Seite gefällt.
Übrigens habe ich noch ein paar weitere interessante Seiten für Sie.)
Hier können Sie das Lösen von Beispielen üben und Ihr Niveau herausfinden. Testen mit sofortiger Verifizierung. Lasst uns lernen – mit Interesse!)
Und hier können Sie Funktionen und Ableitungen kennenlernen.
Regel 1.
Um einen Bruch mit einer natürlichen Zahl zu multiplizieren, müssen Sie seinen Zähler mit dieser Zahl multiplizieren und den Nenner unverändert lassen.
Regel 2.
So multiplizieren Sie einen Bruch mit einem Bruch:
1. Finden Sie das Produkt der Zähler und das Produkt der Nenner dieser Brüche
2. Schreiben Sie das erste Produkt als Zähler und das zweite als Nenner.
Regel 3.
Um gemischte Zahlen zu multiplizieren, müssen Sie sie als unechte Brüche schreiben und dann die Regel zum Multiplizieren von Brüchen verwenden.
Regel 4.
Um einen Bruch durch einen anderen zu dividieren, müssen Sie den Dividenden mit dem Kehrwert des Divisors multiplizieren.
Beispiel 1.
Berechnung

Beispiel 2.
Berechnung
![]()
Beispiel 3.
Berechnung
Beispiel 4.
Berechnung
Mathematik. Andere Materialien
Erhöhen einer Zahl auf eine rationale Potenz. (
Eine Zahl zu einer natürlichen Potenz erhöhen. (
Verallgemeinerte Intervallmethode zur Lösung algebraischer Ungleichungen (Autor A.V. Kolchanov)
Methode zum Ersetzen von Faktoren beim Lösen algebraischer Ungleichungen (Autor Kolchanov A.V.)
Zeichen der Teilbarkeit (Lungu Alena)
Testen Sie sich zum Thema „Multiplikation und Division gewöhnlicher Brüche“
Brüche multiplizieren
Wir werden die Multiplikation gewöhnlicher Brüche in mehreren möglichen Varianten betrachten.
Einen gewöhnlichen Bruch mit einem Bruch multiplizieren
Dies ist der einfachste Fall, in dem Sie Folgendes verwenden müssen Regeln für die Multiplikation von Brüchen.
Zu Bruch mit Bruch multiplizieren, notwendig:
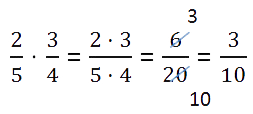
Bevor Sie Zähler und Nenner multiplizieren, prüfen Sie, ob sich die Brüche reduzieren lassen. Durch die Reduzierung von Brüchen in Berechnungen werden Ihre Berechnungen erheblich einfacher.

Einen Bruch mit einer natürlichen Zahl multiplizieren
Einen Bruch machen mit einer natürlichen Zahl multiplizieren Sie müssen den Zähler des Bruchs mit dieser Zahl multiplizieren und den Nenner des Bruchs unverändert lassen.
Wenn das Ergebnis der Multiplikation ein unechter Bruch ist, vergessen Sie nicht, ihn in eine gemischte Zahl umzuwandeln, d. h. den ganzen Teil hervorzuheben.

Gemischte Zahlen multiplizieren
Um gemischte Zahlen zu multiplizieren, müssen Sie sie zunächst in unechte Brüche umwandeln und dann gemäß der Regel zur Multiplikation gewöhnlicher Brüche multiplizieren.

Eine andere Möglichkeit, einen Bruch mit einer natürlichen Zahl zu multiplizieren
Bei Berechnungen ist es manchmal bequemer, eine andere Methode zur Multiplikation eines gewöhnlichen Bruchs mit einer Zahl zu verwenden.
Um einen Bruch mit einer natürlichen Zahl zu multiplizieren, müssen Sie den Nenner des Bruchs durch diese Zahl dividieren und den Zähler gleich lassen.

Wie aus dem Beispiel hervorgeht, ist diese Version der Regel bequemer anzuwenden, wenn der Nenner des Bruchs ohne Rest durch eine natürliche Zahl teilbar ist.
Einen Bruch durch eine Zahl dividieren
Wie dividiert man einen Bruch am schnellsten durch eine Zahl? Lassen Sie uns die Theorie analysieren, eine Schlussfolgerung ziehen und anhand von Beispielen sehen, wie die Division eines Bruchs durch eine Zahl mithilfe einer neuen Kurzregel erfolgen kann.
Normalerweise folgt die Division eines Bruchs durch eine Zahl der Regel zum Teilen von Brüchen. Wir multiplizieren die erste Zahl (Bruch) mit dem Kehrwert der zweiten. Da die zweite Zahl eine ganze Zahl ist, ist ihr Kehrwert ein Bruch, dessen Zähler gleich eins und dessen Nenner gleich der gegebenen Zahl ist. Schematisch sieht die Division eines Bruchs durch eine natürliche Zahl so aus:
![]()
Daraus schließen wir:
Um einen Bruch durch eine Zahl zu dividieren, müssen Sie den Nenner mit dieser Zahl multiplizieren und den Zähler gleich lassen. Die Regel lässt sich noch kürzer formulieren:
Wenn man einen Bruch durch eine Zahl dividiert, geht die Zahl in den Nenner ein.
Teilen Sie einen Bruch durch eine Zahl:

Um einen Bruch durch eine Zahl zu dividieren, schreiben wir den Zähler unverändert um und multiplizieren den Nenner mit dieser Zahl. Wir reduzieren 6 und 3 um 3.

Wenn wir einen Bruch durch eine Zahl dividieren, schreiben wir den Zähler um und multiplizieren den Nenner mit dieser Zahl. Wir reduzieren 16 und 24 um 8.

Wenn man einen Bruch durch eine Zahl dividiert, geht die Zahl in den Nenner ein, also lassen wir den Zähler gleich und multiplizieren den Nenner mit dem Divisor. Wir reduzieren 21 und 35 um 7.
Brüche multiplizieren und dividieren
Beim letzten Mal haben wir gelernt, wie man Brüche addiert und subtrahiert (siehe Lektion „Brüche addieren und subtrahieren“). Der schwierigste Teil dieser Aktionen bestand darin, Brüche auf einen gemeinsamen Nenner zu bringen.
Jetzt ist es an der Zeit, sich mit Multiplikation und Division zu befassen. Die gute Nachricht ist, dass diese Operationen noch einfacher sind als Addition und Subtraktion. Betrachten wir zunächst den einfachsten Fall, wenn es zwei positive Brüche ohne getrennten ganzzahligen Teil gibt.
Um zwei Brüche zu multiplizieren, müssen Sie deren Zähler und Nenner getrennt multiplizieren. Die erste Zahl ist der Zähler des neuen Bruchs und die zweite der Nenner.
Um zwei Brüche zu dividieren, müssen Sie den ersten Bruch mit dem „invertierten“ zweiten Bruch multiplizieren.
Aus der Definition folgt, dass die Division von Brüchen auf eine Multiplikation reduziert wird. Um einen Bruch umzudrehen, tauschen Sie einfach Zähler und Nenner aus. Daher werden wir uns in der gesamten Lektion hauptsächlich mit der Multiplikation befassen.
Durch die Multiplikation kann ein reduzierbarer Bruch entstehen (und entsteht oft auch) – dieser muss natürlich gekürzt werden. Sollte sich nach all den Kürzungen herausstellen, dass der Bruch falsch ist, sollte der ganze Teil hervorgehoben werden. Aber was bei der Multiplikation definitiv nicht passieren wird, ist die Reduktion auf einen gemeinsamen Nenner: keine Kreuzmethoden, größte Faktoren und kleinste gemeinsame Vielfache.
Aufgabe. Finden Sie die Bedeutung des Ausdrucks:
Per Definition haben wir:

Brüche mit ganzen Teilen und negativen Brüchen multiplizieren
Wenn Brüche einen ganzzahligen Teil enthalten, müssen sie in unechte umgewandelt und erst dann nach den oben beschriebenen Schemata multipliziert werden.
Steht im Zähler eines Bruchs, im Nenner oder davor ein Minus, kann es nach folgenden Regeln aus der Multiplikation herausgenommen oder ganz entfernt werden:
- Plus durch Minus ergibt Minus;
- Zwei Negative ergeben ein Bejahendes.
- Wir streichen die Negative paarweise durch, bis sie vollständig verschwinden. Im Extremfall kann ein Minus überleben – dasjenige, für das es keinen Partner gab;
- Wenn keine Minuspunkte mehr übrig sind, ist die Operation abgeschlossen – Sie können mit der Multiplikation beginnen. Wenn das letzte Minus nicht durchgestrichen ist, weil es dafür kein Paar gab, nehmen wir es außerhalb der Multiplikationsgrenzen. Das Ergebnis ist ein negativer Bruch.
Bisher sind diese Regeln nur beim Addieren und Subtrahieren negativer Brüche anzutreffen, wenn es darum ging, den ganzen Teil loszuwerden. Für eine Arbeit können sie verallgemeinert werden, um mehrere Nachteile gleichzeitig zu „verbrennen“:
Wir wandeln alle Brüche in unechte Brüche um und entfernen dann die Minuspunkte aus der Multiplikation. Was übrig bleibt, multiplizieren wir nach den üblichen Regeln. Wir bekommen:

Ich möchte Sie noch einmal daran erinnern, dass das Minuszeichen, das vor dem Bruch erscheint, hervorgehoben ist ganzer Teil bezieht sich speziell auf den gesamten Bruch und nicht nur auf seinen ganzen Teil (dies gilt für die letzten beiden Beispiele).
Beachten Sie auch negative Zahlen: Beim Multiplizieren werden sie in Klammern gesetzt. Dies geschieht, um die Minuszeichen von den Multiplikationszeichen zu trennen und die gesamte Notation genauer zu machen.
Brüche im laufenden Betrieb reduzieren
Die Multiplikation ist ein sehr arbeitsintensiver Vorgang. Die Zahlen fallen hier recht groß aus, und um das Problem zu vereinfachen, können Sie versuchen, den Bruch weiter zu reduzieren vor der Multiplikation. Tatsächlich sind Zähler und Nenner von Brüchen im Wesentlichen gewöhnliche Faktoren und können daher mithilfe der Grundeigenschaft eines Bruchs reduziert werden. Schauen Sie sich die Beispiele an:
![]()

In allen Beispielen sind die reduzierten Zahlen und deren Reste rot markiert.
Bitte beachten Sie: Im ersten Fall wurden die Multiplikatoren vollständig reduziert. An ihre Stelle treten Einheiten, die im Allgemeinen nicht geschrieben werden müssen. Im zweiten Beispiel konnte zwar keine vollständige Reduzierung erreicht werden, der Gesamtaufwand an Berechnungen verringerte sich aber dennoch.
Wenden Sie diese Technik jedoch niemals beim Addieren und Subtrahieren von Brüchen an! Ja, manchmal gibt es ähnliche Zahlen, die man einfach reduzieren möchte. Hier, schau:
Das kannst du nicht machen!
Der Fehler tritt auf, weil beim Addieren der Zähler eines Bruchs eine Summe und kein Produkt von Zahlen ergibt. Folglich ist es unmöglich, die Grundeigenschaft eines Bruchs anzuwenden, da es sich bei dieser Eigenschaft speziell um die Multiplikation von Zahlen handelt.
Es gibt einfach keine anderen Gründe, Brüche zu kürzen, daher sieht die richtige Lösung des vorherigen Problems so aus:
Wie Sie sehen, war die richtige Antwort nicht so schön. Seien Sie im Allgemeinen vorsichtig.
Brüche dividieren.
Einen Bruch durch eine natürliche Zahl dividieren.
Beispiele für die Division eines Bruchs durch eine natürliche Zahl
Division einer natürlichen Zahl durch einen Bruch.
Beispiele für die Division einer natürlichen Zahl durch einen Bruch
Division gewöhnlicher Brüche.
Beispiele für die Division gewöhnlicher Brüche
Gemischte Zahlen dividieren.
- Um eine gemischte Zahl durch eine andere zu dividieren, müssen Sie Folgendes tun:
- gemischte Brüche in unechte Brüche umwandeln;
- Multipliziere den ersten Bruch mit dem Kehrwert des zweiten;
- den resultierenden Bruch reduzieren;
- Wenn Sie einen unechten Bruch erhalten, wandeln Sie den unechten Bruch in einen gemischten Bruch um.
- gemischte Brüche in unechte Brüche umwandeln;
- Multiplizieren der Zähler und Nenner von Brüchen;
- Reduziere den Bruch;
- Wenn Sie einen unechten Bruch erhalten, wandeln wir den unechten Bruch in einen gemischten Bruch um.
- Unter und unter Überarbeitetes Lied „Frühlingstango“ (Die Zeit kommt – Vögel fliegen aus dem Süden) – Musik. Valery Milyaev Ich habe nicht genug gehört, ich habe es nicht verstanden, ich habe es nicht verstanden, in dem Sinne, dass ich es nicht erraten habe, ich habe alle Verben untrennbar mit geschrieben, ich wusste nichts über das Präfix nedo. Es passiert, […]
- Seite nicht gefunden In der dritten Schlusslesung wurde ein Paket von Regierungsdokumenten angenommen, die die Schaffung von Sonderverwaltungsregionen (SAR) vorsehen. Durch den Austritt aus der Europäischen Union wird das Vereinigte Königreich nicht in den europäischen Mehrwertsteuerraum einbezogen und […]
- Der Gemeinsame Untersuchungsausschuss wird im Herbst erscheinen. Der Gemeinsame Untersuchungsausschuss wird im Herbst erscheinen. Die Ermittlungen aller Strafverfolgungsbehörden werden im vierten Anlauf unter einem Dach zusammengefasst. Bereits im Herbst 2014, so Iswestija, Präsident Wladimir Putin [ …]
- Patent für einen Algorithmus Wie ein Patent für einen Algorithmus aussieht Wie ein Patent für einen Algorithmus erstellt wird Vorbereitung technische Beschreibungen Methoden zur Speicherung, Verarbeitung und Übertragung von Signalen und/oder Daten speziell für Patentierungszwecke bereiten in der Regel keine besonderen Schwierigkeiten und […]
- Was ist über den neuen Gesetzentwurf zu Renten vom 12. Dezember 1993 zu wissen? Verfassung der Russischen Föderation (unter Berücksichtigung der Änderungen durch die Gesetze der Russischen Föderation über Änderungen der Verfassung der Russischen Föderation vom 30. Dezember 2008 N 6- FKZ, vom 30.12.2008 N 7-FKZ, […]
- Lustige Lieder über die Rente einer Frau für den Helden des Tages, Männer für den Helden des Tages, Männer - im Chor für den Helden des Tages, Frauen - Widmung an Rentner, Frauen, humorvoll. Wettbewerbe für Rentner werden interessant sein. Moderator : Liebe Freunde! Einen Augenblick! Sensation! Nur […]
Beispiele für die Division gemischter Zahlen
1 1 2: 2 2 3 = 1 2 + 1 2: 2 3 + 2 3 = 3 2: 8 3 = 3 2 3 8 = 3 3 2 8 = 9 16
2 1 7: 3 5 = 2 7 + 1 7: 3 5 = 15 7: 3 5 = 15 7 5 3 = 15 5 7 3 = 5 5 7 = 25 7 = 7 3 + 4 7 = 3 4 7
Alle obszönen Kommentare werden gelöscht und ihre Autoren werden auf die schwarze Liste gesetzt!
Willkommen bei OnlineMSchool.
Mein Name ist Dovzhik Mikhail Viktorovich. Ich bin der Besitzer und Autor dieser Seite, ich habe das gesamte theoretische Material geschrieben und außerdem Online-Übungen und Taschenrechner entwickelt, die Sie zum Mathematiklernen verwenden können.
Brüche. Brüche multiplizieren und dividieren.
Einen gewöhnlichen Bruch mit einem Bruch multiplizieren.
Um gewöhnliche Brüche zu multiplizieren, müssen Sie den Zähler mit dem Zähler (wir erhalten den Zähler des Produkts) und den Nenner mit dem Nenner (wir erhalten den Nenner des Produkts) multiplizieren.
Formel zur Multiplikation von Brüchen:


Bevor Sie mit der Multiplikation von Zählern und Nennern beginnen, müssen Sie prüfen, ob der Bruch reduziert werden kann. Wenn Sie den Bruch reduzieren können, können Sie weitere Berechnungen einfacher durchführen.
Beachten Sie! Hier muss nicht nach einem gemeinsamen Nenner gesucht werden!!
Einen gemeinsamen Bruch durch einen Bruch dividieren.
Die Division eines gewöhnlichen Bruchs in einen Bruch erfolgt folgendermaßen: Drehen Sie den zweiten Bruch um (d. h. ändern Sie Zähler und Nenner) und anschließend werden die Brüche multipliziert.
Formel zum Teilen gewöhnlicher Brüche:


Einen Bruch mit einer natürlichen Zahl multiplizieren.
Beachten Sie! Bei der Multiplikation eines Bruchs mit einer natürlichen Zahl wird der Zähler des Bruchs mit unserer natürlichen Zahl multipliziert und der Nenner des Bruchs bleibt gleich. Wenn das Ergebnis des Produkts ein unechter Bruch ist, markieren Sie unbedingt den gesamten Teil und verwandeln Sie den unechten Bruch in einen gemischten Bruch.

Division von Brüchen mit natürlichen Zahlen.
Es ist nicht so beängstigend, wie es scheint. Wie bei der Addition wandeln wir die ganze Zahl in einen Bruch mit Eins im Nenner um. Zum Beispiel:

Gemischte Brüche multiplizieren.
Regeln zum Multiplizieren von Brüchen (gemischt):
Beachten Sie! Um einen gemischten Bruch mit einem anderen gemischten Bruch zu multiplizieren, müssen Sie ihn zunächst in die Form unechter Brüche umwandeln und dann gemäß der Regel zur Multiplikation gewöhnlicher Brüche multiplizieren.

Die zweite Möglichkeit, einen Bruch mit einer natürlichen Zahl zu multiplizieren.
Es kann bequemer sein, die zweite Methode zu verwenden, bei der ein gemeinsamer Bruch mit einer Zahl multipliziert wird.
Beachten Sie! Um einen Bruch mit einer natürlichen Zahl zu multiplizieren, müssen Sie den Nenner des Bruchs durch diese Zahl dividieren und den Zähler unverändert lassen.

Aus dem obigen Beispiel wird deutlich, dass diese Option bequemer zu verwenden ist, wenn der Nenner eines Bruchs ohne Rest durch eine natürliche Zahl dividiert wird.
Mehrstöckige Brüche.
In der Oberstufe trifft man häufig auf dreistöckige (oder mehrstöckige) Brüche. Beispiel:
Um einen solchen Bruch in seine übliche Form zu bringen, verwenden Sie die Division durch 2 Punkte:

Beachten Sie! Bei der Division von Brüchen ist die Reihenfolge der Division sehr wichtig. Seien Sie vorsichtig, hier kann man leicht verwirrt werden.
Beachten Sie, Zum Beispiel:
Wenn man eins durch einen beliebigen Bruch dividiert, ist das Ergebnis derselbe Bruch, nur invertiert:
Praktische Tipps zum Multiplizieren und Dividieren von Brüchen:
1. Das Wichtigste bei der Arbeit mit gebrochenen Ausdrücken ist Genauigkeit und Aufmerksamkeit. Führen Sie alle Berechnungen sorgfältig und genau, konzentriert und klar durch. Es ist besser, ein paar zusätzliche Zeilen in Ihren Entwurf zu schreiben, als sich in gedanklichen Berechnungen zu verlieren.
2. Wechseln Sie bei Aufgaben mit verschiedenen Brucharten zu den gewöhnlichen Brüchen.
3. Wir reduzieren alle Brüche, bis eine Reduzierung nicht mehr möglich ist.
4. Wir wandeln mehrstufige Bruchausdrücke durch Division durch 2 Punkte in gewöhnliche um.




