Isolierter Funktionspunkt. Laurent-Reihe isolierte singuläre Punkte und ihre Klassifizierung

Taylor rangiert beim Aufschlag wirksame Mittel zum Studium analytischer Funktionen in einem Kreis zol Für das Studium analytischer Funktionen in einem Ringgebiet erweist es sich als möglich, Entwicklungen in positiven und negativen Potenzen (z - zq) der Form zu konstruieren, die Taylor-Entwicklungen verallgemeinern. Die Reihe (1), verstanden als Summe zweier Reihen, wird Laurent-Reihe genannt. Es ist klar, dass der Konvergenzbereich der Reihe (1) der gemeinsame Teil der Konvergenzbereiche jeder Reihe (2) ist. Lasst uns sie finden. Der Konvergenzbereich der ersten Reihe ist ein Kreis, dessen Radius durch die Cauchy-Hadamard-Formel bestimmt wird. Innerhalb des Konvergenzkreises konvergiert die Reihe (3) zu einer analytischen Funktion und in jedem Kreis mit kleinerem Radius konvergiert sie absolut und gleichmäßig. Die zweite Reihe ist eine Potenzreihe bezüglich einer Variablen. Reihe (5) konvergiert innerhalb ihres Konvergenzkreises gegen die analytische Funktion einer komplexen Variablen m-*oo, und in jedem Kreis mit kleinerem Radius konvergiert sie absolut und gleichmäßig, was bedeutet, dass der Konvergenzbereich der Reihen (4) das Äußere des Kreises ist – wenn dann ein gemeinsamer Konvergenzbereich der Reihen (3) und (4) vorhanden ist – ein Kreisring, in dem Reihe (1) konvergiert zu einer analytischen Funktion. Darüber hinaus konvergiert es in jedem Ring absolut und gleichmäßig. Beispiel 1. Bestimmen Sie den Konvergenzbereich der Rad-Laurent-Reihe. Isolierte singuläre Punkte und ihre Klassifizierung M. Der Konvergenzbereich der ersten Reihe ist das Äußere des Kreises und der Konvergenzbereich der zweiten Reihe ist das Innere des Kreises. Somit gilt: diese Reihe konvergiert zu Kreisen Satz 15. Jede Funktion f (z), eindeutig und unpolitisch in einem Kreisring, kann in diesem Ring als Summe einer konvergenten Reihe dargestellt werden, deren Koeffizienten Cn eindeutig bestimmt und nach den Formeln berechnet werden wobei 7p ein Kreis mit dem Radius m ist. Lassen Sie uns einen beliebigen Punkt z innerhalb des Rings R festlegen. Konstruieren wir Kreise mit Mittelpunkten im Punkt r, deren Radien die Ungleichungen erfüllen, und betrachten wir einen neuen Ring. Unter Verwendung des Integralsatzes von Cauchy für einen mehrfach zusammenhängenden Bereich haben wir Folgendes: Wir transformieren jedes der Integrale in der Summe (8) separat. Für alle Punkte £ entlang des Kreises 7d* ist die Summenrelation der gleichmäßig konvergenten Reihe 1 1 erfüllt. Daher kann der Bruch ^ durch vi- /" / Multiplikation beider Teile mit dargestellt werden kontinuierliche Funktion (O und die Term-für-Term-Integration entlang des Kreises durchführen, stellen wir fest, dass wir die Transformation des zweiten Integrals auf etwas andere Weise durchführen werden. Für alle Punkte £ auf dem Kreis ir> ist die Beziehung erfüllt. Daher gilt: Der Bruch ^ kann als Summe einer gleichmäßig konvergenten Reihe dargestellt werden. Durch Multiplikation beider Teile mit einer stetigen Funktion und termweiser Integration entlang des Kreises 7/ erhalten wir Folgendes: Beachten Sie, dass die Integranden in den Formeln (10) und (12) analytische Funktionen sind in einem kreisförmigen Ring. Daher ändern sich aufgrund des Satzes von Cauchy die Werte der entsprechenden Integrale nicht, wenn wir die Kreise 7/r und 7r/ durch einen beliebigen Kreis ersetzen. Dadurch können wir die Formeln (10) und (12) kombinieren. Durch Ersetzen der Integrale auf der rechten Seite der Formel (8) durch ihre Ausdrücke (9) bzw. (11) erhalten wir die erforderliche Entwicklung. Da z beliebig ist Punkt des Rings folgt daraus, dass die Reihe ( 14) überall in diesem Ring gegen die Funktion f(z) konvergiert, und in jedem Ring konvergiert die Reihe absolut und gleichmäßig gegen diese Funktion. Beweisen wir nun, dass die Zerlegung der Form (6) eindeutig ist. Nehmen wir an, dass es eine weitere Entwicklung gibt. Dann gilt überall im Ring R: Auf dem Kreis konvergieren die Reihen (15) gleichmäßig. Multiplizieren wir beide Seiten der Gleichheit (wobei m eine feste ganze Zahl ist) und integrieren wir beide Reihen Term für Term. Als Ergebnis erhalten wir auf der linken Seite und auf der rechten Seite - Sch. Also (4, = St. Da m ist eine beliebige Zahl, die letzte Gleichheit beweist die Eindeutigkeit der Entwicklung. Die Reihe (6), deren Koeffizienten mit den Formeln (7) berechnet werden, wird als Laurent-Reihe der Funktion f(z) im Ring bezeichnet. Die Die Menge der Terme dieser Reihe mit nichtnegativen Potenzen wird als regulärer Teil der Laurent-Reihe bezeichnet, und mit negativen als deren Hauptteil. Formeln ( 7) für die Koeffizienten der Laurent-Reihe werden in der Praxis selten verwendet, weil, als In der Regel erfordern sie umständliche Berechnungen. Normalerweise werden, wenn möglich, vorgefertigte Taylor-Entwicklungen von Elementarfunktionen verwendet. Basierend auf der Eindeutigkeit der Entwicklung führt jede legale Technik zum gleichen Ergebnis. Beispiel 2 Betrachten Sie die Laurent-Reihenentwicklungen von Funktionen in verschiedenen Bereichen, vorausgesetzt, dass f(r) zwei singuläre Punkte hat: Folglich gibt es drei ringförmige Bereiche, die im Punkt r = 0 zentriert sind. In jedem von ihnen ist die Funktion f(r) analytisch: a ) Kreisring außerhalb des Kreis (Abb. 27). Finden wir die Laurent-Entwicklungen der Funktion /(z) in jedem dieser Bereiche. Stellen wir /(z) als Summe elementarer Brüche dar a) Kreis Wir transformieren Beziehung (16) wie folgt. Unter Verwendung der Formel für die Summe der Terme einer geometrischen Folge erhalten wir. Ersetzen Sie die gefundenen Erweiterungen in Formel (17) : Diese Entwicklung ist die Taylor-Reihe der Funktion /(z). b) Der Ring für die Funktion -r bleibt in diesem Ring konvergent, da Reihe (19) für die Funktion j^j für |z| > 1 divergiert. Daher transformieren wir die Funktion /(z) wie folgt: Wiederum unter Anwendung der Formel (19) erhalten wir, dass diese Reihe für konvergiert. Wenn wir die Erweiterungen (18) und (21) in die Beziehung (20) einsetzen, erhalten wir c) Das Äußere des Kreises für die Funktion -z für |z| > 2 divergiert, und Reihe (21) für die Funk- Stellen wir die Funktion /(z) in der folgenden Form dar: /<*>Mit den Formeln (18) und (19) erhalten wir OR 1. Dieses Beispiel zeigt, dass die Laurent-Entwicklung im Allgemeinen für dieselbe Funktion f(z) gilt andere Art für verschiedene Ringe. Beispiel 3. Finden Sie die Entwicklung der 8. Laurent-Reihe einer Funktion Laurent-Reihe. Isolierte singuläre Punkte und ihre Klassifizierung in einem Ringbereich A. Wir verwenden die Darstellung der Funktion f(z) in der folgenden Form: und transformieren den zweiten Term mit Formel für die Summe der Terme einer geometrischen Folge erhalten wir. Wenn wir die gefundenen Ausdrücke in die Formel (22) einsetzen, erhalten wir Beispiel 4. Erweitern Sie die Funktion in der Laurent-Reihe am Punkt zq = 0. Für jeden Komplex haben wir Put This Die Erweiterung gilt für jeden Punkt z Ф 0. In in diesem Fall Der ringförmige Bereich stellt die gesamte komplexe Ebene mit einem herausgeworfenen Punkt z - 0 dar. Dieser Bereich kann durch die folgende Beziehung definiert werden: Diese Funktion ist im Bereich analytisch. Aus den Formeln (13) für die Koeffizienten der Laurent-Reihe unter Verwendung derselben Wenn man wie im vorherigen Absatz argumentiert, kann man die Ungleichungen Kouiw erhalten. wenn die Funktion f(z) auf einem Kreis beschränkt ist, wobei M eine Konstante ist), dann Isolierte singuläre Punkte Der Punkt zo heißt isolierter singulärer Punkt der Funktion f(z), wenn es eine Ringumgebung des Punktes gibt ( Diese Menge wird manchmal als punktierte Umgebung des Punktes 2o bezeichnet, in der die Funktion f(z) eindeutig und analytisch ist. Am Punkt zo selbst ist die Funktion entweder undefiniert oder nicht eindeutig und analytisch. Abhängig vom Verhalten der Funktion /(r) bei Annäherung an den Punkt zo werden drei Arten von singulären Punkten unterschieden. Ein isolierter singulärer Punkt heißt: 1) entfernbar, wenn es einen endlichen gibt, 2) pmusach, wenn 3) ein im Wesentlichen singulärer Punkt, wenn die Funktion f(z) keinen Grenzwert hat. Der Typ eines isolierten singulären Punktes hängt eng mit dem zusammen Natur der Laurent-Erweiterung der Funktion durch das punktierte Zentrum von . Satz 16. Ein isolierter singulärer Punkt z0 einer Funktion f(z) ist genau dann ein entfernbarer singulärer Punkt, wenn die Laurent-Entwicklung der Funktion f(z) in einer Umgebung des Punktes zo keinen Hauptteil enthält, d. h. hat die Form Sei zo ein entfernbarer singulärer Punkt. Dann gibt es eine endliche Funktion, daher ist die Funktion f(z) in einer prokologischen Umgebung des Punktes z beschränkt. Wir setzen: Aufgrund der Cauchyschen Ungleichungen können alle Koeffizienten bei negativen Potenzen (z - 20) gleich Null sind: Umgekehrt sei Laurent, dass die Entwicklung der Funktion /(r) in einer Umgebung des Punktes zq nur den richtigen Teil enthält, das heißt, sie hat die Form (23) und ist daher Taylor. Es ist leicht zu erkennen, dass für z -* z0 die Funktion /(z) einen Grenzwert hat: Satz 17. Ein isolierter singulärer Punkt zq der Funktion f(z) ist genau dann entfernbar, wenn die Funktion J(z) ist in einer punktierten Umgebung des Punktes zq begrenzt, Zgmechai nicht. Sei r ein abnehmbarer singulärer Punkt der Funktion /(r). Nehmen wir an, wir erhalten, dass die Funktion /(r) in einem Kreis analytisch ist, dessen Mittelpunkt im Punkt r liegt. Dies bestimmt den Namen des Punktes – entfernbar. Satz 18. Ein isolierter singulärer Punkt zq einer Funktion f(z) ist genau dann ein Pol, wenn der Hauptteil der Laurent-Entwicklung der Funktion f(z) in einer Umgebung des Punktes eine endliche (und positive) Zahl enthält von Termen ungleich Null, d.h. e. hat die Form 4 Sei z0 ein Pol. Seitdem gibt es eine punktierte Umgebung des Punktes z0, in der die Funktion f(z) analytisch und ungleich Null ist. Dann wird in dieser Umgebung eine analytische Funktion definiert und daher ist der Punkt zq ein entfernbarer singulärer Punkt (Nullpunkt) der Funktion oder wobei h(z) eine analytische Funktion ist, h(z0) Φ 0. Dann ist h(zo) Φ 0 ebenfalls analytisch ist, dann ist die Funktion φ in einer Umgebung des Punktes zq analytisch, und daher erhalten wir daraus Folgendes: Nehmen wir nun an, dass die Funktion f(z) eine Entwicklung der Form (24) in einer punktierten Umgebung von hat der Punkt zо. Dies bedeutet, dass in dieser Umgebung die Funktion f(z) zusammen mit der Funktion analytisch ist. Für die Funktion g(z) gilt die Entwicklung, aus der ersichtlich ist, dass zq ein entfernbarer singulärer Punkt der Funktion g(z) ist und existiert. Dann ist die Funktion bei 0 tendenziell der Pol der Funktion. Dort ist eine weitere einfache Tatsache. Der Punkt Zq ist genau dann ein Pol der Funktion f(z), wenn die Funktion g(z) = yj durch Setzen von g(z0) = 0 auf eine analytische Funktion in einer Umgebung des Punktes zq erweitert werden kann. Die Ordnung des Pols der Funktion f(z) heißt nullte Ordnung der Funktion jfa. Die folgende Aussage ergibt sich aus den Sätzen 16 und 18. Satz 19. Ein isolierter singulärer Punkt ist genau dann im Wesentlichen singulär, wenn der Hauptteil der Laurent-Entwicklung in einer punktierten Umgebung dieses Punktes unendlich viele von Null verschiedene Terme enthält. Beispiel 5. Der singuläre Punkt der Funktion ist zo = 0. Wir haben isolierte singuläre Punkte der Laurent-Reihe und ihre Klassifizierung. Daher ist zo = O ein entfernbarer singulärer Punkt. Die Entwicklung der Funktion /(z) zu einer Laurent-Reihe in der Nähe des Nullpunktes enthält nur den richtigen Teil: Beispiel7. /(z) = Der singuläre Punkt der Funktion f(z) ist zq = 0. Betrachten wir das Verhalten dieser Funktion auf der realen und imaginären Achse: auf der realen Achse bei x 0, auf der imaginären Achse Folglich dort ist weder ein endlicher noch ein unendlicher Grenzwert für f(z) bei z -* 0 existiert nicht. Das bedeutet, dass der Punkt r = 0 ein im Wesentlichen singulärer Punkt der Funktion f(z) ist. Finden wir die Laurent-Entwicklung der Funktion f(z) in der Nähe des Nullpunkts. Für jedes komplexe C gilt Set. Dann enthält die Laurent-Entwicklung unendlich viele Terme mit negativen Potenzen von z.

Grundlegende Konzepte und Definitionen:

Der Nullpunkt der analytischen Funktion f(z) ist der Punkt „a“, für den f(a)=0.

Eine Nullstelle der Ordnung „n“ einer Funktion f(z) ist ein Punkt „a“, wenn fn(a)¹0.

Ein singulärer Punkt „a“ heißt isolierter singulärer Punkt einer Funktion f(z), wenn es eine Umgebung dieses Punktes gibt, in der es außer „a“ keine singulären Punkte gibt.

Es gibt drei Arten isolierter singulärer Punkte: .

1 abnehmbare Einzelpunkte;

3 im Wesentlichen einzigartige Punkte.

Der Typ des singulären Punktes kann anhand des Verhaltens einer gegebenen Funktion am gefundenen singulären Punkt sowie anhand der Form der Laurent-Reihe bestimmt werden, die für die Funktion in der Umgebung des gefundenen singulären Punktes erhalten wurde.

Bestimmen des Typs eines singulären Punktes anhand des Verhaltens der Funktion an ihm.

1. Abnehmbare Einzelpunkte.

Ein isolierter singulärer Punkt a einer Funktion f(z) heißt abnehmbar, wenn es einen endlichen Grenzwert gibt.

2.Pole.

Ein isolierter singulärer Punkt a einer Funktion f(z) heißt Pol if .

3. Im Wesentlichen singuläre Punkte.

Ein isolierter singulärer Punkt a einer Funktion f(z) heißt im Wesentlichen singulärer Punkt, wenn weder endlich noch unendlich existiert.

Zwischen den Nullstellen und Polen der Funktion besteht die folgende Beziehung.

Damit Punkt a ein Pol der Ordnung n der Funktion f(Z) ist, ist es notwendig und ausreichend, dass dieser Punkt eine Nullstelle der Ordnung n für die Funktion ist.

Wenn n=1, heißt der Pol einfach.

Definition: Ein isolierter singulärer Punkt eindeutiger Natur heißt:

a) entfernbar, wenn der Hauptteil der Zerlegung fehlt;

b) ein Pol, wenn der Hauptteil endlich viele Terme enthält;

c) ein im Wesentlichen singulärer Punkt, wenn der Hauptteil unendlich viele Terme enthält.

a) In der Umgebung eines entfernbaren singulären Punktes hat die Entwicklung also die Form:

es drückt die Funktion an allen Punkten des Kreises |z-a| aus

Im Zentrum z=a ist die Gleichheit nicht wahr, weil Die Funktion bei z=a hat eine Diskontinuität und die rechte Seite ist stetig. Wenn der Wert der Funktion in der Mitte geändert wird, sodass er dem Wert auf der rechten Seite entspricht, wird die Lücke beseitigt – daher der Name – entfernbar.

b) In der Umgebung eines Pols der Ordnung m hat die Laurent-Reihenentwicklung die Form:

c) In der Nähe eines einfachen Pols

Abzüge und Formeln zu ihrer Berechnung.

Der Rest einer analytischen Funktion f(z) an einem isolierten singulären Punkt z 0 ist eine komplexe Zahl, die dem Wert des Integrals entspricht , genommen in positiver Richtung entlang des Kreises L mit Mittelpunkt im Punkt z 0, der im Analysebereich der Funktion f(z) liegt (d. h. im Ring 0).<|z-z0|

Der Rest der Funktion f(z) an einem isolierten singulären Punkt z 0 wird mit dem Symbol Res f(z 0) oder Res (f(z); z 0) bezeichnet. Auf diese Weise,

Res f(z 0)= . (22.15.1)

Wenn wir n=-1 in Formel (22.15.1) einsetzen, erhalten wir:

C -1 =

oder Res f(z 0)= C -1 ,

diese. der Rest der Funktion f(z) in Bezug auf den singulären Punkt z 0 ist gleich dem Koeffizienten des ersten Termes mit negativem Exponenten in der Entwicklung der Funktion f(z) in der Laurent-Reihe.

Berechnung der Abzüge.

Regelmäßige oder abnehmbare Einzelpunkte. Wenn z=z 0 ein regulärer oder entfernbarer singulärer Punkt der Funktion f(z) ist, dann ist Res f(z 0)=0 (der Laurent-Entwicklung fehlt in diesen Fällen der Hauptteil, also c-1=0) .

Pole. Der Punkt z 0 sei ein einfacher Pol der Funktion f(z). Dann hat die Laurent-Reihe für die Funktion f(z) in der Nähe des Punktes z 0 die Form:

Von hier

Wenn wir also diese Gleichheit an den Grenzwert bei z - z 0 übergeben, erhalten wir

Res f(z0)=

Im Wesentlichen ein besonderer Punkt. Wenn der Punkt z 0 ein im Wesentlichen singulärer Punkt der Funktion f(z) ist, wird zur Berechnung des Rests der Funktion an diesem Punkt normalerweise der Koeffizient c-1 in der Laurent-Reihenentwicklung der Funktion direkt bestimmt.

Klassifizierung von Ereignissen. Summe, Produkt von Ereignissen, ihre Eigenschaften, grafische Darstellung.

Die Veranstaltungen sind unterteilt in:

1. Zufällig

2. Zuverlässig

3. Unmöglich

Zuverlässig ist ein Ereignis, das unter bestimmten Bedingungen (die Nacht folgt dem Morgen) notwendigerweise eintritt.

Ein Zufallsereignis ist ein Ereignis, das eintreten kann oder auch nicht (das Bestehen einer Prüfung).

Ein unmögliches Ereignis ist ein Ereignis, das unter bestimmten Bedingungen nicht eintreten wird (ein grüner Stift aus einer Schachtel mit nur roten Stiften).

Modelle, die durch Systeme zweier autonomer Differentialgleichungen beschrieben werden.

Phasenebene. Phasenporträt. Isoclin-Methode. Hauptisoklinen. Stabilität des stationären Zustands. Lineare Systeme. Arten von singulären Punkten: Knoten, Sattel, Fokus, Zentrum. Beispiel: Chemische Reaktionen erster Ordnung.

Die interessantesten Ergebnisse zur qualitativen Modellierung der Eigenschaften biologischer Systeme wurden mit Modellen zweier Differentialgleichungen erzielt, die eine qualitative Forschung mit der Methode ermöglichen Phasenebene. Betrachten wir ein System aus zwei autonomen gewöhnlichen Differentialgleichungen allgemeiner Form

(4.1)

P(x,y), Q(x,y)- Kontinuierliche Funktionen, die in einem bestimmten Bereich definiert sind G Euklidische Ebene ( x,y- Kartesische Koordinaten) und in diesem Bereich stetige Ableitungen der Ordnung haben, die nicht niedriger als die erste sind.

Region G kann entweder unbegrenzt oder begrenzt sein. Wenn die Variablen x, y haben eine bestimmte biologische Bedeutung (Stoffkonzentrationen, Artenzahlen), am häufigsten das Gebiet G stellt den positiven Quadranten der rechten Halbebene dar:

0 £ X< ¥ ,0 £ j< ¥ .

Konzentrationen von Stoffen oder Artenzahlen können auch von oben durch das Volumen des Gefäßes oder die Fläche des Lebensraums begrenzt werden. Dann hat der Variablenbereich die Form:

0 £ X< x 0 , 0 £ j< y 0 .

Variablen x, y zeitliche Änderung gemäß dem Gleichungssystem (4.1), so dass jeder Zustand des Systems einem Paar variabler Werte entspricht ( x, y).

Umgekehrt ist jedes Variablenpaar ( x, y) entspricht einem bestimmten Zustand des Systems.

Stellen Sie sich eine Ebene mit Koordinatenachsen vor, auf der die Werte der Variablen aufgetragen sind x,y. Jeder Punkt M Diese Ebene entspricht einem bestimmten Zustand des Systems. Diese Ebene wird Phasenebene genannt und stellt die Gesamtheit aller Zustände des Systems dar. Der Punkt M(x,y) wird als darstellender oder darstellender Punkt bezeichnet.

Lassen Sie es im ersten Moment der Zeit t=t 0 Koordinaten des darstellenden Punktes M 0 (X(T 0), ja(T 0)). In jedem nächsten Moment T Der darstellende Punkt verschiebt sich entsprechend den Änderungen der Werte der Variablen X(T), ja(T). Sammeln von Punkten M(X(T), y(t)) auf der Phasenebene, deren Position den Zuständen des Systems im Prozess der zeitlichen Änderung von Variablen entspricht x(t), y(t) nach den Gleichungen (4.1) heißt Phasenbahn.

Der Satz von Phasentrajektorien für verschiedene Anfangswerte der Variablen ergibt ein gut sichtbares „Porträt“ des Systems. Konstruktion Phasenporträt ermöglicht es Ihnen, Rückschlüsse auf die Art von Änderungen in Variablen zu ziehen x, y ohne Kenntnis analytischer Lösungen des ursprünglichen Gleichungssystems(4.1).

Um ein Phasenporträt darzustellen, ist es notwendig, an jedem Punkt der Phasenebene ein Vektorfeld der Richtungen der Systemtrajektorien zu konstruieren. Schrittweite einstellenD t>0,wir erhalten die entsprechenden Inkremente D X Und D j aus Ausdrücken:

D x=P(x,y)D T,

D y=Q(x,y)D T.

Vektorrichtung dy/dx am Punkt ( x, y) hängt vom Vorzeichen der Funktionen ab P(x, y), Q(x, y) und kann durch eine Tabelle angegeben werden:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Lösung dieser Gleichung y = y(x,c), oder implizit F(x,y)=c, Wo Mit– Integrationskonstante, ergibt die Familie der Integralkurven der Gleichung (4.2) – Phasentrajektorien System (4.1) im Flugzeug x, y.

Isoklinenmethode

Um ein Phasenporträt zu erstellen, verwenden sie Isoklinenmethode – Auf der Phasenebene werden Linien gezeichnet, die die Integralkurven in einem bestimmten Winkel schneiden. Die Isoklinengleichung lässt sich leicht aus (4.2) erhalten. Lasst uns

Wo A– einen bestimmten konstanten Wert. Bedeutung A stellt den Tangens des Neigungswinkels der Tangente an die Phasentrajektorie dar und kann Werte annehmen von –¥ bis + ¥ . Stattdessen ersetzen dy/dx in (4.2) die Menge A wir erhalten die Isoklinengleichung:

.(4.3)

Gleichung (4.3) definiert an jedem Punkt der Ebene eine eindeutige Tangente an die entsprechende Integralkurve, mit Ausnahme des Punktes wo P(x,y)= 0, Q (x,y) = 0 , bei dem die Richtung der Tangente unsicher wird, da der Wert der Ableitung unsicher wird:

Dieser Punkt ist der Schnittpunkt aller Isoklinen - besonderer Punkt. Dabei verschwinden gleichzeitig die zeitlichen Ableitungen der Variablen X Und j.

Somit sind an einem singulären Punkt die Änderungsraten der Variablen Null. Folglich entspricht der singuläre Punkt der Differentialgleichungen der Phasentrajektorien (4.2). stationärer Zustand des Systems(4.1) und seine Koordinaten sind die stationären Werte der Variablen x, y.

Von besonderem Interesse sind Hauptisoklinen:

dy/dx=0, P(x,y)=0 – Isokline horizontaler Tangenten und

dy/dx=¥ ,Q(x,y)=0 – Isokline vertikaler Tangenten.

Durch Konstruieren der Hauptisoklinen und Finden ihres Schnittpunkts (x,y), deren Koordinaten die Bedingungen erfüllen:

Wir finden damit den Schnittpunkt aller Isoklinen der Phasenebene, in dem die Richtung der Tangenten an die Phasentrajektorien ungewiss ist. Das - singulärer Punkt, was entspricht stationärer Zustand des Systems(Abb. 4.2).

Das System (4.1) hat so viele stationäre Zustände, wie es Schnittpunkte der Hauptisoklinen auf der Phasenebene gibt.

Jede Phasentrajektorie entspricht einer Reihe von Bewegungen eines dynamischen Systems, die dieselben Zustände durchlaufen und sich nur am Anfang der Zeitzählung voneinander unterscheiden.

Wenn die Bedingungen des Satzes von Cauchy erfüllt sind, dann durch jeden Punkt im Raum x, y, t Es gibt nur eine Integralkurve. Das Gleiche gilt aufgrund der Autonomie auch für Phasentrajektorien: Eine einzelne Phasentrajektorie verläuft durch jeden Punkt der Phasenebene.

Steady-State-Stabilität

Lassen Sie das System im Gleichgewichtszustand sein.

Dann liegt der darstellende Punkt an einem der singulären Punkte des Systems, an dem per Definition gilt:

Ob ein einzelner Punkt stabil ist oder nicht, wird dadurch bestimmt, ob der darstellende Punkt den stationären Zustand mit einer kleinen Abweichung verlässt oder nicht. In Bezug auf ein System aus zwei Gleichungen ist die Definition von Stabilität in der Sprachee, Dwie folgt.

Der Gleichgewichtszustand ist stabil, wenn ein bestimmter Bereich von Abweichungen vom Gleichgewichtszustand vorliegt (e )Sie können den Bereich angeben D (e ), den Gleichgewichtszustand umgibt und die Eigenschaft hat, dass keine Flugbahn innerhalb der Region beginnt D , wird niemals die Grenze erreichen e . (Abb. 4.4)

Für eine große Klasse von Systemen - grobe Systeme – Da sich die Art ihres Verhaltens bei einer kleinen Änderung der Form der Gleichungen nicht ändert, können Informationen über die Art des Verhaltens in der Nähe eines stationären Zustands dadurch gewonnen werden, dass nicht das Original, sondern ein vereinfachtes untersucht wird linearisiert System.

Lineare Systeme.

Betrachten Sie ein Zweiersystem lineare Gleichungen:

.(4.4)

Hier A B C D- Konstanten, x, y- Kartesische Koordinaten auf der Phasenebene.

Wir suchen nach einer allgemeinen Lösung in der Form:

.(4.5)

Setzen wir diese Ausdrücke in (4.4) ein und reduzieren um e l T:

(4.6)

Algebraisches Gleichungssystem (4.6) mit Unbekannten A, B hat nur dann eine Lösung ungleich Null, wenn ihre Determinante, bestehend aus Koeffizienten für die Unbekannten, gleich Null ist:

Wenn wir diese Determinante erweitern, erhalten wir die charakteristische Gleichung des Systems:

.(4.7)

Das Lösen dieser Gleichung ergibt die Exponentenwertel 1,2 , für die Werte ungleich Null möglich sind A Und B Lösungen für Gleichung (4.6). Diese Bedeutungen sind

.(4.8)

Wenn der radikale Ausdruck negativ ist, dannl 1,2 komplexe konjugierte Zahlen. Nehmen wir an, dass beide Wurzeln der Gleichung (4.7) Realteile ungleich Null haben und dass es keine Mehrfachwurzeln gibt. Dann kann die allgemeine Lösung des Systems (4.4) als lineare Kombination von Exponentialfunktionen mit Exponenten dargestellt werdenl 1 , l 2 :

(4.9)

Um die Natur möglicher Trajektorien des Systems auf der Phasenebene zu analysieren, verwenden wir lineare homogene Koordinatentransformation, was das System dazu führen wird kanonische Form:

,(4.10)

Dies ermöglicht eine bequemere Darstellung auf der Phasenebene im Vergleich zum ursprünglichen System (4.4). Lassen Sie uns neue Koordinaten einführenξ , η nach den Formeln:

(4.1)

Aus dem Verlauf der linearen Algebra ist bekannt, dass bei Ungleichheit die Realteile Null werdenl 1 , l 2 Das ursprüngliche System (4.4) kann jederzeit mithilfe von Transformationen (4.11) in die kanonische Form (4.10) umgewandelt und sein Verhalten auf der Phasenebene untersucht werdenξ , η . Betrachten wir die verschiedenen Fälle, die hier auftreten können.

Wurzeln λ 1 , λ 2 – gültig und vom gleichen Vorzeichen

In diesem Fall sind die Transformationskoeffizienten real, wir bewegen uns von der realen Ebenex,yzur realen Ebene ξ, η. Wenn wir die zweite der Gleichungen (4.10) durch die erste dividieren, erhalten wir:

.(4.12)

Wenn wir diese Gleichung integrieren, finden wir:

Wo .(4.13)

Lassen Sie uns unter λ verstehen 2 die Wurzel der charakteristischen Gleichung mit einem großen Modul, was die Allgemeingültigkeit unserer Argumentation nicht verletzt. Dann, da im betrachteten Fall die Wurzeln λ 1 , λ 2 – gültig und vom gleichen Vorzeichen,A>1 , und wir haben es mit Integralkurven parabolischen Typs zu tun.

Alle Integralkurven (außer der Achse η , was entspricht ) berühren den Ursprung der Achse ξ, welches auch die Integralkurve der Gleichung (4.11) ist. Der Koordinatenursprung ist ein besonderer Punkt.

Lassen Sie uns nun die Bewegungsrichtung des darstellenden Punktes entlang der Phasentrajektorien herausfinden. Wenn λ 1 , λ 2 sind dann, wie aus den Gleichungen (4.10) ersichtlich ist, |ξ|, |η| mit der Zeit abnehmen. Der darstellende Punkt nähert sich dem Koordinatenursprung, erreicht ihn aber nie. Andernfalls würde dies dem Satz von Cauchy widersprechen, der besagt, dass durch jeden Punkt der Phasenebene nur eine Phasentrajektorie verläuft.

Solch ein besonderer Punkt, durch den Integralkurven verlaufen, genau wie eine Familie von Parabeln verläuft durch den Ursprung und wird Knoten genannt (Abb. 4.5)

Gleichgewichtszustand des Knotentyps bei λ 1 , λ 2 < 0 ist Lyapunov stabil, da sich der darstellende Punkt entlang aller Integralkurven in Richtung des Koordinatenursprungs bewegt. Das stabiler Knoten. Wenn λ 1 , λ 2 > 0 also |ξ|, |η| nehmen mit der Zeit zu und der darstellende Punkt entfernt sich vom Koordinatenursprung. In diesem Fall der besondere Punkt– instabiler Knoten .

Auf der Phasenebene x, y die allgemeine qualitative Natur des Verhaltens von Integralkurven bleibt erhalten, aber die Tangenten an die Integralkurven fallen nicht mit den Koordinatenachsen zusammen. Der Neigungswinkel dieser Tangenten wird durch das Verhältnis der Koeffizienten bestimmt α , β , γ , δ in den Gleichungen (4.11).

Wurzeln λ 1 , λ 2 – sind gültig und haben unterschiedliche Vorzeichen.

Konvertieren von Koordinaten x,y zu Koordinaten ξ, η wieder echt. Die Gleichungen für die kanonischen Variablen haben wieder die Form (4.10), aber jetzt die Vorzeichen von λ 1 , λ 2 sind anders. Die Gleichung der Phasentrajektorien hat die Form:

Wo ,(4.14)

Integrieren wir (4.14), finden wir

(4.15)

Das Die Gleichung definiert eine Kurvenschar vom hyperbolischen Typ, bei der beide Koordinatenachsen vorliegen– Asymptoten (at A=1 wir hätten eine Familie gleichseitiger Hyperbeln). Die Koordinatenachsen sind in diesem Fall ebenfalls Integralkurven– Dies sind die einzigen Integralkurven, die durch den Ursprung verlaufen. Jededavon besteht aus drei Phasentrajektorien: zweier Bewegungen in einen Gleichgewichtszustand (bzw. aus einem Gleichgewichtszustand) und aus einem Gleichgewichtszustand. Alle anderen Integralkurven– sind Hyperbeln, die nicht durch den Ursprung gehen (Abb. 4.6) Dieser besondere Punkt heißt "Sattel ». Niveaulinien in der Nähe eines Bergsattels verhalten sich ähnlich wie Phasentrajektorien in der Nähe eines Sattels.

Betrachten wir die Art der Bewegung des darstellenden Punktes entlang Phasentrajektorien in der Nähe des Gleichgewichtszustands. Lassen Sie zum Beispielλ 1 >0 , λ 2<0 . Dann wird der darstellende Punkt auf die Achse gelegt ξ , wird vom Ursprung wegbewegt und auf der Achse platziert η – wird sich dem Koordinatenursprung auf unbestimmte Zeit nähern, ohne es in endlicher Zeit zu erreichen. Überall dort, wo sich der darstellende Punkt im Anfangsmoment befindet (mit Ausnahme des singulären Punktes und der Punkte auf der Asymptote). η =0), es wird sich irgendwann vom Gleichgewichtszustand entfernen, auch wenn es sich zunächst entlang einer der Integralkurven in Richtung des singulären Punktes bewegt.

Es ist klar, dass Ein einzelner Punkt wie ein Sattel ist immer instabil . Nur unter speziell gewählten Anfangsbedingungen an der Asymptoteη =0 Das System nähert sich einem Gleichgewichtszustand. Dies widerspricht jedoch nicht der Aussage über die Instabilität des Systems. Wenn wir zählen, dass alle Anfangszustände des Systems auf der Phasenebene gleich wahrscheinlich sind, dann ist die Wahrscheinlichkeit eines solchen Anfangszustands, der einer Bewegung in die Richtung entspricht Zu Singularpunkt ist gleich Null. Daher wird jede reale Bewegung das System aus dem Gleichgewichtszustand bringen.Zurück zu den Koordinatenx,y,wir erhalten das gleiche qualitative Bild der Art der Bewegung von Trajektorien um den Koordinatenursprung.

Die Grenze zwischen den betrachteten Fällen eines Knotens und eines Sattels ist der Fall Wann zum Beispiel einer der charakteristischen Indikatoren λ 1 , verschwindet, was auftritt, wenn die Determinante des Systems- Ausdruck ad-bc=0(siehe Formel 4.8 ). In diesem Fall sind die Koeffizienten der rechten Seiten der Gleichungen (4.4) proportional zueinander:

und das System hat als Gleichgewichtszustände alle Punkte der Linie:

Die verbleibenden Integralkurven sind eine Schar paralleler Geraden mit einem Winkelkoeffizienten , entlang derer sich die darstellenden Punkte je nach Vorzeichen der zweiten Wurzel der charakteristischen Gleichung λ entweder dem Gleichgewichtszustand nähern oder von diesem entfernen 2 = a+d.(Abb.4.7 ) In diesem Fall hängen die Koordinaten des Gleichgewichtszustands vom Anfangswert der Variablen ab.

Wurzeln λ 1 , λ 2 – Komplexkonjugieren

In diesem Fall tatsächlichX Und j wir werden haben komplexe Konjugate ξ , η (4.10) . Durch die Einführung einer weiteren Zwischentransformation ist es jedoch auch in diesem Fall möglich, die Betrachtung auf eine echte lineare homogene Transformation zu reduzieren. Lasst uns:

(4.16)

Wo a,b, Und u, v – tatsächliche Werte. Es kann gezeigt werden, dass die Transformation vonx,y Zu u, v ist unter unseren Annahmen reell, linear, homogen mit einer von Null verschiedenen Determinante. Aufgrund der Gleichungen(4.10, 4.16) gilt:

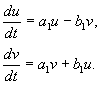(4.17)

Division der zweiten Gleichung durch die erste, wir bekommen:

was einfacher zu integrieren ist, wenn wir zum Polarkoordinatensystem gehen (R, φ ) . Nach der Auswechslung wir kommen von wo:

.(4.18)

Also auf der Phasenebenedu, vwir haben es mit einer Familie logarithmischer Spiralen zu tun, von denen jede hatasymptotischer Punkt im Ursprung.Ein singulärer Punkt, der der asymptotische Punkt aller Integralkurven ist, die die Form einer Spirale haben, in jedem verschachteltFreund, es heißt Fokus ( Abb.4.8 ) .

Betrachten wir die Art der Bewegung des darstellenden Punktes entlang Phasentrajektorien. Multiplikation der ersten der Gleichungen (4.17) mitu, und der zweite weiter v und wenn wir hinzufügen, erhalten wir:

Lassen A 1 < 0 (A 1 = Reλ ) . Der darstellende Punkt nähert sich dann kontinuierlich dem Koordinatenursprung, ohne ihn zu einem endlichen Zeitpunkt zu erreichen. Dies bedeutet, dass die Phasentrajektorien verdrehte Spiralen sind und gedämpften Schwingungen entsprechen Variablen. Das - stetiger Fokus .

Bei einem stabilen Fokus ist wie bei einem stabilen Knoten nicht nur die Lyapunov-Bedingung erfüllt, sondern auch eine strengere Anforderung. Das heißt, dass das System bei anfänglichen Abweichungen im Laufe der Zeit so weit wie gewünscht zur Gleichgewichtsposition zurückkehren wird. Eine solche Stabilität, bei der die anfänglichen Abweichungen nicht nur nicht zunehmen, sondern gegen Null tendieren, wird als Stabilität bezeichnet absolute Stabilität .

Wenn in der Formel (4.18) A 1 >0 , dann bewegt sich der darstellende Punkt vom Ursprung weg, und wir haben es mit zu tun instabiler Fokus . Beim Verlassen eines Flugzeugsu, vzur PhasenebeneX, jAuch die Spiralen bleiben Spiralen, werden aber verformt.

Betrachten wir nun den Fall, wannA 1 =0 . Phasenbahnen im Flugzeugdu, vEs wird Kreise geben welche im Flugzeugx,yentsprechen Ellipsen:

Also wanneine 1=0 durch einen besonderen Punktx= 0, y= 0 es verläuft keine Integralkurve. Ein solcher isolierter singulärer Punkt, in dessen Nähe die Integralkurven geschlossene Kurven, insbesondere ineinander eingebettete Ellipsen sind und den singulären Punkt umschließen, wird als Zentrum bezeichnet.

Somit sind je nach Art der Wurzeln der charakteristischen Gleichung (4.7) sechs Arten von Gleichgewichtszuständen möglich. Ansicht von Phasentrajektorien in einer Ebene x, y für diese sechs Fälle ist in Abb. dargestellt. 4.9.

Reis. 4.9.Arten von Phasenporträts in der Nähe eines stationären Zustands für ein lineares Gleichungssystem (4.4).

Die fünf Arten von Gleichgewichtszuständen sind grob; ihr Charakter ändert sich nicht bei ausreichend kleinen Änderungen auf der rechten Seite der Gleichungen (4.4). In diesem Fall sollten die Änderungen nicht nur auf den rechten Seiten, sondern auch in deren Ableitungen erster Ordnung gering sein. Der sechste Gleichgewichtszustand – die Mitte – ist nicht rau. Bei kleinen Änderungen der Parameter auf der rechten Seite der Gleichungen wird es zu einem stabilen oder instabilen Fokus.

Bifurkationsdiagramm

Führen wir die folgende Notation ein:

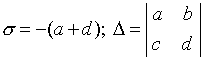. (4.11)

Dann wird die charakteristische Gleichung wie folgt geschrieben:

. (4.12)

Betrachten Sie eine Ebene mit rechtwinkligen kartesischen Koordinaten S , D und markieren Sie darauf die Bereiche, die dem einen oder anderen Gleichgewichtszustandstyp entsprechen, der durch die Art der Wurzeln der charakteristischen Gleichung bestimmt wird

.(4.13)

Voraussetzung für die Stabilität des Gleichgewichtszustandes ist das Vorhandensein eines negativen Realteils von yl 1 und l 2 . Eine notwendige und hinreichende Bedingung hierfür ist die Erfüllung der UngleichungenS > 0, D > 0 . Im Diagramm (4.15) entspricht diese Bedingung Punkten, die im ersten Viertel der Parameterebene liegen. Ein einzelner Punkt wird ein Fokus sein, wennl 1 und l 2 Komplex. Diese Bedingung entspricht den Punkten der Ebene, für die , diese. Punkte zwischen zwei Ästen einer ParabelS 2 = 4 D. Achspunkte S = 0, D>0, entsprechen Gleichgewichtszuständen vom Zentrumstyp. Ebenfalls,l 1 und l 2 - sind gültig, aber von unterschiedlichem Vorzeichen, d.h. Ein singulärer Punkt ist ein Sattel, wenn D<0, usw. Als Ergebnis erhalten wir ein Diagramm der Aufteilung der Parameterebene S, D, in Bereiche, die verschiedenen Arten von Gleichgewichtszuständen entsprechen.

Reis. 4.10. Bifurkationsdiagramm

für ein lineares Gleichungssystem 4.4

Wenn die Koeffizienten des linearen Systems A B C D hängen von einem bestimmten Parameter ab. Wenn sich dieser Parameter ändert, ändern sich auch die WerteS , D . Beim Überschreiten der Grenzen verändert sich der Charakter des Phasenporträts qualitativ. Daher werden solche Grenzen als Bifurkationsgrenzen bezeichnet – auf gegenüberliegenden Seiten der Grenze weist das System zwei topologisch unterschiedliche Phasenporträts und dementsprechend zwei unterschiedliche Verhaltensweisen auf.

Das Diagramm zeigt, wie es zu solchen Veränderungen kommen kann. Wenn wir Sonderfälle – den Koordinatenursprung – ausschließen, ist leicht zu erkennen, dass sich der Sattel beim Überqueren der Ordinatenachse in einen stabilen oder instabilen Knoten verwandeln kann. Ein stabiler Knoten kann entweder in einen Sattel oder in einen stabilen Fokus usw. gehen. Beachten Sie, dass die Übergänge stabiler Knoten – stabiler Fokus und instabiler Knoten – instabiler Fokus keine Bifurkationen sind, da sich die Topologie des Phasenraums nicht ändert. Wir werden in Vorlesung 6 mehr über Phasenraumtopologie und Bifurkationsübergänge sprechen.

Bei Bifurkationsübergängen ändert sich die Art der Stabilität eines einzelnen Punktes. Beispielsweise kann ein stabiler Fokus durch die Mitte zu einem instabilen Fokus werden. Diese Bifurkation heißt Andronov-Hopf-Bifurkation mit den Namen der Wissenschaftler, die es untersucht haben. Während dieser Bifurkation in nichtlinearen Systemen entsteht ein Grenzzyklus und das System gerät in Selbstschwingung (siehe Vorlesung 8).

Beispiel. Lineares chemisches Reaktionssystem

Substanz X strömt von außen mit konstanter Geschwindigkeit, verwandelt sich in Stoff Y und zwar mit einer Geschwindigkeit, die proportional zur Konzentration des Stoffes ist Y, wird aus der Reaktionssphäre entfernt. Alle Reaktionen sind erster Ordnung, mit Ausnahme des Stoffzuflusses von außen, der nullter Ordnung ist. Das Reaktionsschema sieht so aus:

(4.14)

und wird durch das Gleichungssystem beschrieben:

(4.15)

Wir erhalten stationäre Konzentrationen, indem wir die rechten Seiten mit Null gleichsetzen:

.(4.16)

Betrachten wir das Phasenporträt des Systems. Teilen wir die zweite Gleichung des Systems (4.16) durch die erste. Wir bekommen:

.(4.17)

Gleichung (4.17) bestimmt das Verhalten von Variablen auf der Phasenebene. Lassen Sie uns ein Phasenporträt dieses Systems erstellen. Zeichnen wir zunächst die Hauptisoklinen auf der Phasenebene. Gleichung der Isokline vertikaler Tangenten:

Gleichung der Isokline horizontaler Tangenten:

Der singuläre Punkt (stationärer Zustand) liegt im Schnittpunkt der Hauptisoklinen.

Bestimmen wir nun, in welchem Winkel sich die Koordinatenachsen mit den Integralkurven schneiden.

Wenn x= 0, dann .

Somit ist die Tangente der Tangente an die Integralkurven y=y(x), die Ordinatenachse schneidet x=0, ist in der oberen Halbebene negativ (denken Sie daran, dass die Variablen x, y haben Konzentrationswerte, und deshalb interessieren wir uns nur für den oberen rechten Quadranten der Phasenebene). In diesem Fall nimmt der Tangens des Tangentenwinkels mit der Entfernung vom Ursprung zu.

Betrachten Sie die Achse y= 0. Im Schnittpunkt dieser Achse mit den Integralkurven werden diese durch die Gleichung beschrieben

Bei der Tangens der Steigung der Integralkurven, die die Abszissenachse kreuzen, ist positiv und steigt mit zunehmender Zahl von Null auf Unendlich X.

Bei .

Bei weiterem Anstieg nimmt dann der Tangens des Neigungswinkels im Absolutwert ab, bleibt negativ und tendiert zu -1 bei X ® ¥ . Wenn man die Richtung der Tangenten an die Integralkurven auf den Hauptisoklinen und auf den Koordinatenachsen kennt, ist es einfach, das Gesamtbild der Phasentrajektorien zu konstruieren.

Lassen Sie uns die Art der Stabilität des singulären Punktes mit der Lyapunov-Methode ermitteln. Die charakteristische Determinante des Systems hat die Form:

Durch Erweiterung der Determinante erhalten wir die charakteristische Gleichung des Systems: , d.h. Die Wurzeln der charakteristischen Gleichung sind beide negativ. Folglich ist der stationäre Zustand des Systems ein stabiler Knoten. In diesem Fall die Konzentration des Stoffes X tendiert immer monoton zu einem stationären Zustand, die Konzentration des Stoffes Y kann min oder max durchlaufen. Oszillationsmodi sind in einem solchen System unmöglich.

Lassen zq ist der singuläre Punkt der Funktion /(r), t.s. f(z) ist aber an dieser Stelle analytisch (insbesondere darf es an dieser Stelle noch nicht definiert werden). Wenn es eine solche punktierte Umgebung des Punktes gibt zq (d. h. die Menge O z - zq f(z) ist also aialitisch zo angerufen isolierter singulärer Punkt Funktionen f(z). Diese Definition bleibt im Fall von gleich zn = oo, wenn das Jod in der Nähe des Punktes durchbohrt wird zq = oo verstehe set z> ICH - das Äußere eines Kreises, dessen Mittelpunkt im Ursprung liegt. Mit anderen Worten, ein besonderer Punkt zq heißt isoliert, wenn es eine Umgebung dieses Punktes gibt, in der die Liste anderer singulärer Punkte außer ist zq. Im Folgenden betrachten wir nur singuläre Punkte mit eindeutigem Charakter (der Funktion). f(z) als eindeutig vorausgesetzt).

Abhängig vom Verhalten der Funktion f(z) bei z -> zq Es gibt drei Arten von Singularpunkten. Isolierter singulärer Punkt zq-Funktionen f(z) angerufen:

1) abnehmbarer einzelner Punkt, wenn es einen endlichen Grenzwert gibt

2) Pole, wenn es eine Grenze gibt

3) im Wesentlichen ein besonderer Punkt, Wenn f(z) hat weder einen endlichen noch einen unendlichen Grenzwert z-> zq.

Beispiel 26.1. Zeigen wir, dass alle drei Arten von singulären Punkten realisiert sind. Lassen Sie uns überlegen F(z)= Punkt zq = 0 ist isoliert

Besonderheit dieser Funktion. Mit der Formel (22.12) erhalten wir die Entwicklung

woraus folgt, dass es lim gibt fi(z)= 1. Daher ist zq = 0

ist ein entfernbarer singulärer Punkt der Funktion fi(z).

Funktion f‘j(z) =---hat eine Stange an einer Spitze zo= 1 weil

2 R" X

Betrachten wir nun die Funktion )з(z)= e 1 ^ r und zeige das zo = O ist ein im Wesentlichen singulärer Punkt dieser Funktion. Beim Streben z auf Null entlang der reellen Achse die linken und rechten Grenzen der Funktion /z (z) anders: lim Mit 1 / 1 = 0, lim s 1 /* = os. Dies impliziert,

x->0-0 x->0+O

Was f:i(z) hat bei 2 weder eine endliche noch eine unendliche Grenze -> Oh, das ist. zq = O ist ein im Wesentlichen singulärer Punkt dieser Funktion. (Beachten Sie, dass der Punkt tendiert z - iy auf Null entlang der imaginären Achsenfunktion

hat überhaupt keine Begrenzung.)

Es gibt natürlich nicht isolierte singuläre Punkte. Zum Beispiel. Die Funktion hat Pole an Punkten z n = -, P= ±1, ±2,...

Somit, Zq = 0 ist ein nicht isolierter singulärer Punkt dieser Funktion: In jeder (egal wie kleinen) Umgebung dieses Punktes gibt es andere singuläre Punkte g p.

Lassen zo- endlicher isolierter singulärer Punkt einer Funktion f(z). Dann f(z) ist in einer punktierten Umgebung des 0 Zo-Punktes ähnlich zo Diese Umgebung kann als Ring mit Innenradius r = 0 betrachtet werden. Nach Satz 25.1 gilt in der betrachteten Umgebung die Funktion f(z) kann zu einer Laurent-Reihe (25.2) erweitert werden. Wir werden zeigen, dass das Verhalten der Funktion bei 2 -> zq (d. h. der Typ des singulären Punktes zo) hängt von der Art des Hauptteils der Erweiterung ab (25.2); Dieser Umstand erklärt den Ursprung des Begriffs „Hauptteil“.

Satz 2G.2. Ein isolierter singulärer Punkt zo einer Funktion f(z) ist genau dann entfernbar, wenn die Lorapov-Entwicklung in einer punktierten Umgebung dieses Punktes oid hat

diese. besteht nur aus dem richtigen Teil, und alle Koeffizienten des Hauptteils sind gleich dem Aufzählungszeichen.

Nachweisen. 1. Lass zo- abnehmbarer Einzelpunkt. Beweisen wir die Laurent-Entwicklung der Funktion f(z) hat die Form (26.1). Da der besondere Punkt zo entfernbar, dann gibt es einen endlichen Grenzwert lim f(z) = A. Somit, f(z) ist in einer punktierten Umgebung des 0 z - zq-Punktes begrenzt Zo, diese. )(z) für alle z aus dieser Umgebung. Nehmen wir welche R. U ð /?|, und verwenden Sie die Formeln (25.3) für die Koeffizienten der Laurent-Reihe:

Für die Koeffizienten des Hauptteils der Entwicklung n =- 1,-2,... Für solche Werte P wir haben p~ p-e 0 um R-> 0. Da der Wert R kann dann beliebig klein gewählt werden Herr~" kann beliebig klein sein. Da |s t,| ^ Herr~p und c„ hängen nicht von p ab, dann ist c„ = 0 at Und= - 1, -2,..., was bewiesen werden musste.

2. Nehmen wir nun an, dass die Laurent-Entwicklung die Form (26.1) hat. Die Reihe (26.1) ist eine Potenzreihe und. daher konvergiert es nicht nur im punktierten Bereich, sondern in der gesamten Umgebung z-zq einschließlich des Punktes zo; seine Menge S(z) ist analytisch bei z und S(z) = )(z) bei 0 z - zo R. Daher gibt es einen endlichen Grenzwert )(z)= Pt 5(g) = 5(th) - Daher ist der singuläre Punkt zq

Z->Zo Z-*Zo

abnehmbar. Der Satz ist bewiesen.

Kommentar. Aus dem Beweis des Satzes folgt, dass in einer punktierten Umgebung 0 z - zo eines abnehmbaren singulären Punktes die Funktion f(z) stimmt mit der Funktion 5(r) überein, die in der gesamten Umgebung analytisch ist z - zo. Wenn wir also /(th) = setzen S(zq), dann, ohne die Funktionswerte zu ändern f(z) An jedem Punkt der punktierten Nachbarschaft machen wir diese Funktion in Go analytisch, d. h. Lassen Sie uns die Funktion „eliminieren“. Dies erklärt den Begriff „entfernbares Merkmal“. Es liegt nahe, solche Punkte als reguläre und nicht als singuläre Punkte der Funktion zu betrachten f(z).

Betrachten Sie zum Beispiel die Funktion

In Beispiel 26.1 wurde gezeigt, dass Pm Nr) = 1, d.h. singulärer Punkt

zq = 0 abnehmbar. Wenn wir /i(0) = 1 setzen, eliminieren wir dadurch die Singularität und erhalten eine Funktion, die an diesem Punkt analytisch ist zq = 0 (und in der gesamten C-Ebene).

Lassen Sie uns nun die Pole anhand von Laurent-Entwicklungen charakterisieren.

Satz 26.3. Ein isolierter singulärer Punkt Zo einer Funktion f(z) ist genau dann ein Pol, wenn, wenn der Hauptteil der Laurent-Entwicklung mit Zentrum Zq nur endlich viele verschiedene hat

aus Nullkoeffizienten mit n:

Nachweisen. 1. Lass zq - Pol, d.h. lim/( z) = oo.

Beweisen wir die Laurent-Entwicklung der Funktion f(z) hat die Form (2G.2). Da lim f(z)= oo. dann gibt es eine punktierte Umgebung des Punktes

ki zq. worin f(z) ist analytisch und hat keine Nullen. Dann die Funktion g(z) = 1 /f(z) wird auch in dieser punktierten Nachbarschaft analytisch sein, und lim g(z)= 0. Daher gilt: Zo ist abnehmbar *-? *0

Singularpunkt der Funktion g(z). Definieren wir g(z) am Punkt zo, setzen g(zo)= 0. Dann g(z) wird in der gesamten Umgebung des (nicht durchbohrten) Punktes analytisch z 0 , Und z 0 wird sein isolierter Nullpunkt sein. Bezeichnen wir mit N Multiplizität (Ordnung) dieser Null. Wie in §23 gezeigt wurde, in der Nähe des Punktes zq-Funktion g(z) kann in der Form dargestellt werden (siehe (23.2))

Und (z$) f 0 und y>(z) ist in einer Umgebung des Punktes analytisch zo- Als IP(z) kontinuierlich an einem Punkt zo Und g>(zo) Ф 0" dann IP(z) hat in irgendeiner Umgebung dieses Punktes keine Nullen. Daher Funktion 1 /-p(z) wird auch in dieser Nachbarschaft analytisch sein und entwickelt sich daher darin in einer Taylor-Reihe:

Indem wir die Klammern öffnen und die Bezeichnungen der Koeffizienten ändern, schreiben wir die letzte Erweiterung in das Formular

wobei c_jv = 1>o f 0. Somit enthält der Hauptteil der Laurent-Entwicklung der Funktion /(r) nur eine endliche Anzahl von Termen; wir sind bei der gewünschten Gleichheit angekommen (26.2).

2. Lassen Sie die punktierte Umgebung von Punkten ein Th Funktion )(z) wird durch die Laurent-Entwicklung (26.2) dargestellt (für eine detailliertere Form siehe (26.3)), deren Hauptteil nur eine endliche Anzahl von Termen enthält, und Mit- D" F 0. Das muss bewiesen werden Zq - Funktionspol f(z). Gleichheit (26.3) multiplizieren mit (G - G o) iV , wir erhalten die Funktion

Die Reihe in (26.4) ist eine Potenzreihe, die nicht nur im punktierten Punkt, sondern in der gesamten Umgebung des Punktes gegen eine analytische Funktion konvergiert Zq. Daher die Funktion h(z) wird in dieser Nachbarschaft analytisch, wenn wir es in Go-by-Putting weiter definieren h(zo)= s_dg F 0. Dann

Somit ist der Punkt th ein Pol und Satz 26.3 ist bewiesen.

Multiplizität (Ordnung) der Nullfunktion g(z)= 1//(g) heißt Polordnung te Funktion /(r). Wenn N- die Ordnung des Pols von th also g(z)= (g - Zo) N ip(z), Los geht) F 0, und wie im ersten Teil des Beweises von Satz 26.3 gezeigt, hat die Entwicklung der Funktion /(r) die Form (26.3), wobei c_/v F 0. Umgekehrt, wenn /(r) in die Reihe (26.3) und entwickelt wird e-i F 0 also

t.s. N- Ordnung des Pols der Funktion /(r). Auf diese Weise, Polordnung der zq-Funktion/(G) gleich der Zahl des höchsten Koeffizienten ungleich Null des Hauptteils der Laurent-Entwicklung in der punktierten Umgebung des Punktes zq(d. h. gleich dieser Zahl N, Was für ein Mist F 0 und Sp= 0 bei P > N).

Lassen Sie uns die folgende Aussage beweisen, die für Anwendungen praktisch ist.

Folgerung 26.4. Der Punkt zq ist ein Pol der Ordnung N der Fiktion/(G) dann und nur wann/(G) in der Form darstellbar

wobei h(z) eine analytische Funktion in der Umgebung des Punktes ist Th und h(zo) f 0.

Nachweisen. Funktion cp(z) = l/h(z) ist in einer Umgebung des Punktes h analytisch. Die Bedingung von Korollar 26.4 ist äquivalent zu Folgendem:

Deshalb zq - Nullmultiplizität N Funktionen g(z). und daher der Pol der Vielfalt N Funktionen /(2).

II Beispiel 26.5. Finden Sie isolierte singuläre Punkte einer Funktion und ihren Typ bestimmen.

Lösung: Die Punkte, an denen (z 2 + 1 )(z+ Z) 2 = 0. Wenn z 2 L- 1 = 0, dann 2 = ±g Wenn (z 4- 3) 2 = 0, dann z= -3. Daher hat die Funktion drei singuläre Punkte z= g, 22 = -g, Z3 = - 3. Überlegen Sie z:

G - Pol erster Ordnung (wir haben Korollar 26.4 verwendet). Auf ähnliche Weise lässt sich beweisen, dass 22 = -ich auch ein Pol erster Ordnung. Für 2z haben wir:

Betrachten wir nun grundsätzlich einzelne Punkte.

Satz 26.6. Ein isolierter singulärer Punkt zq einer Funktion f(z) ist genau dann im Wesentlichen singulär, wenn der Hauptteil der Laurent-Entwicklung mit dem Zentrum zq unendlich viele verschiedene Punkte hat. Null, Koeffizienten von p.

Nachweisen. Satz 26.6 folgt direkt aus den Sätzen 26.2 und 26.3. In der Tat, wenn der Punkt zq im Wesentlichen speziell ist, kann der Hauptteil der Laurent-Entwicklung nicht fehlen oder eine endliche Anzahl von Termen enthalten (andernfalls der Punkt). Zq ist entweder abnehmbar oder eine Stange). Daher muss die Anzahl der Terme im Hauptteil unendlich sein.

Umgekehrt, wenn der Hauptteil unendlich viele Begriffe enthält, dann Zq kann weder ein abnehmbarer Punkt noch ein Pol sein. Daraus folgt, dass dieser Punkt im Wesentlichen etwas Besonderes ist.

Laut Definition ist ein im Wesentlichen singulärer Punkt dadurch gekennzeichnet, dass die Funktion /(2) weder einen endlichen noch einen unendlichen Grenzwert für hat z ->zq. Eine umfassendere Vorstellung davon, wie unregelmäßig das Verhalten einer Funktion in der Nähe eines im Wesentlichen singulären Punktes ist, liefert der folgende Satz.

Satz 26.7 (Sokhotskys Satz). Wenn zq für Personen wesentlich ist, ist der Punkt der Funktion f(z), dann für irgendjemanden komplexe Zahl L, einschließlich A = Oh, Es gibt eine Folge von Punkten z n mit z n -> zo und lim f(zn) = A.

p->os

Nachweisen. Betrachten wir zunächst den Fall A = ooh. Im ersten Teil des Beweises von Satz 2G.2 haben wir festgestellt, dass if f(z) in einer punktierten Umgebung des Punktes r begrenzt ist, dann sind alle Koeffizienten c", n = - 1,- 2,... des Hauptteils sind gleich Null (und daher ist die Singularität in go entfernbar). Da th gemäß der Bedingung ein wesentlicher singulärer Punkt ist, ist die Funktion f(r) in jeder punktierten Umgebung des Punktes th unbeschränkt. Nehmen wir eine solche starke Umgebung 0 Z f(zi) > 1 (wenn |/(r)| z - zo I/2 gibt es einen Punkt z-2 , wobei |/(yy)| > 2 usw.: in der punktierten Nachbarschaft O 71. Es ist offensichtlich, dass r„ -e go und lim /(r“) = oo. Für den Fall A = oo gilt also Satz 26.7

bewiesen.

Lass es jetzt Ein f ooh. Nehmen wir zunächst an, dass es eine punktierte Umgebung 0 gibt

= -yy---- wird in dieser punktierten Nachbarschaft analytisch sein und folglich

/(G) - A

Folglich ist go ein isolierter singulärer Punkt der Funktion Φ(r). Wir zeigen es Ihnen. dass r ein im Wesentlichen singulärer Punkt von Φ(r) ist. Das stimmt möglicherweise nicht. Dann gibt es einen Grenzwert lim Ф(r), endlich oder unendlich. Für eine Weile

/(r) = A + , dann gibt es auch Hsh /(r), was der Bedingung widerspricht

F(g) ~ :-*z 0

Ich verstehe den Satz. Somit ist r0 ein im Wesentlichen singulärer Punkt der Funktion Φ(r). Gemäß dem, was oben bewiesen wurde, gibt es eine Folge von Punkten r n mit r n th und lim Ф(r n) = oo. Von hier

Wir haben die erforderliche Aussage unter der Annahme bewiesen, dass /(r) F A in einer punktierten Umgebung des Punktes go- Nehmen wir nun an, dass dies falsch ist, d. h. In jeder beliebig kleinen punktierten Umgebung des Punktes gibt es einen solchen Punkt G", dass /(r") = L. Dann für jeden P in der punktierten Umgebung 0 f(z u) = À. Somit ist die gewünschte Aussage wahr P-Yuo

in allen Fällen und Satz 26.7 ist bewiesen.

Nach Satz 26.7 (Sokhotsky) nimmt die Funktion /(r) in jeder (beliebig kleinen) punktierten Umgebung eines im Wesentlichen singulären Punktes Werte an, die beliebig nahe an einer beliebigen Zahl aus der erweiterten komplexen Ebene C liegen.

Zur Untersuchung isolierter singulärer Punkte sind oft die bereits bekannten Taylor-Entwicklungen grundlegender Elementarfunktionen nützlich.

Beispiel 2G.8. Bestimmen Sie den Typ des singulären Punkts zq = 0 für die Funktion

Gelöst und e. Erweitern wir den Zähler und den Nenner zu einer Taylor-Reihe in Potenzen von g. Ersetzen wir in (22.11) 3 z Anstatt r zu verwenden und 1 zu subtrahieren, erhalten wir

Mit (22.12) erhalten wir die Entwicklung des Nenners:

Die Reihen in diesen Erweiterungen konvergieren in der gesamten komplexen Ebene €. Wir haben

und /2(2) sind in einer Umgebung des Punktes anaritisch zo = 0 (und sogar in der gesamten Ebene) und /2(20) F 0 also h(z) ist auch in einer Umgebung des Punktes gF 0 analytisch. Nach Korollar 26.4 ist der Punkt Zo = 0 ist der Pol der Ordnung N=4.

II Beispiel 26.9. Finden Sie singuläre Punkte einer Funktion f(z)= sin j - und bestimmen Sie ihren Typ.

R e in e i e. Die Funktion hat einen einzigen endlichen singulären Punkt zq = 1. An anderen Punkten von C die Funktion w =--- analytisch; daher die Funktion sin w wird analytisch sein.

Wenn wir - anstelle von r in die Sinusentwicklung (22.12) einsetzen, erhalten wir

Wir haben die Entwicklung der Funktion sin in eine Laurent-Reihe in einer punktierten Umgebung des Punktes 2o = 1 erhalten. Da die resultierende Entwicklung unendlich viele Terme mit negativen Potenzen (r - 1) enthält, dann zq = 1 ist ein im Wesentlichen singulärer Punkt (in diesem Fall besteht die Laurent-Entwicklung nur aus dem Hauptteil und der reguläre Teil fehlt).

Beachten Sie, dass es in diesem Fall möglich war, die Natur der Singularität direkt aus der Definition zu ermitteln, ohne auf Reihenentwicklung zurückzugreifen. Tatsächlich gibt es Folgen (r'') und (2''), die gegen konvergieren zo= 1, und so das f(z"n)= 1, /(2") = 0 (geben Sie solche Sequenzen selbst an). Also, f(z) hat keine Begrenzung z -> 1 und daher Punkt zq - 1 ist im Wesentlichen etwas Besonderes.

Lassen Sie uns das Konzept der Laurent-Entwicklung einer Funktion in der Umgebung eines Punktes einführen Zq = 00 und betrachten Sie an dieser Stelle den Zusammenhang zwischen der Entwicklung und der Natur der Singularität. Beachten Sie, dass die Definitionen eines isolierten singulären Punktes und seines Typs (entfernbar, Pol oder im Wesentlichen singulär) auf den Fall übertragen werden zq = oc ohne Änderungen. Aber Satz 26.2. 26.3 und 26.6, die sich auf die Art der Laurent-Erweiterungen beziehen, müssen geändert werden. Der Punkt ist, dass Mitglieder cn(z- 2o) S. P= -1,-2,..., Hauptteil, der die „Unregelmäßigkeit“ der Funktion in der Nähe des Endpunkts definiert Zq, da 2 zu oo tendiert, werden sie sich „richtig“ verhalten (zu 0 tendieren). Im Gegenteil, die Mitglieder des richtigen Teils mit P= 1,2,... tendiert zu oo; Sie bestimmen die Art des Merkmals in Zq = oo. Daher wird der Hauptteil der Expansion in der Umgebung von oo aus Termen mit positiver Potenz bestehen P, und das richtige - mit negativen.

Lassen Sie uns eine neue Variable einführen w = 12. Funktion tv = 1/2, erweitert so dass u(oo) = 0, eins zu eins und bildet die Nachbarschaft konform ab z > R Punkte zq = 00 in der Nähe von |w| wq = 0. Wenn die Funktion f(z) Analytik in der punktierten Nachbarschaft R z Zq = oc, dann ist die Funktion G(w) = f(l/w) wird in der großen Nachbarschaft 0 wo = 0 analytisch sein. Da es bei 2 -> oo sein wird w-> 0 also

Deshalb G(w) hat auf den Punkt wq = 0 ist ein Merkmal vom gleichen Typ wie f(z) am Punkt Zq = 00. Entwickeln wir die Funktion G(w) zu einer Laurent-Reihe in einer punktierten Umgebung des Punktes wo = 0:

Die Summen auf der rechten Seite von (26.5) repräsentieren den regulären bzw. den Hauptteil der Entwicklung. Kommen wir zur Variablen z, ersetzen w = 1/z:

Bezeichnen P= -A*, 6* = 6_„ = s p und das zu bemerken G(l/z) = f(z), wir bekommen

Die Zerlegung (2G.G) heißt Laurent-Entwicklung der Funktion f(z) in einer punktierten Umgebung des Punktes zq= oo. Die erste Summe in (2G.6) heißt der richtige Teil, und die zweite Summe ist Hauptteil dieser Zersetzung. Da diese Summen den richtigen und Hauptteilen der Entwicklung (26.5) entsprechen, gelten für die Entwicklung (26.6) Analoga der Sätze 26.2, 26.3 und 26.6. Somit ist der folgende Satz ein Analogon zu Satz 26.2.

Satz 26.10. Isolierter singulärer PunktZq - Betriebssystem (Funktionen/(G) ist genau dann entfernbar, wenn die Laurent-Entwicklung in einer punktierten Umgebung dieses Punktes die Form hat

t.s. besteht nur aus dem richtigen Teil.

Setzen wir /(oo) = co. Funktion definiert durch die in der Nachbarschaft konvergierende Reihe (26.7). z > R Punkt 2o = oc, genannt analytisch am Punkt z o = oo. (Beachten Sie, dass diese Definition der Analytizität der Funktion entspricht G(w) am Punkt wo = 0.)

Beispiel 26.11. Untersuchen Sie den singulären Punkt zq = oo der Funktion

Da der Grenzwert also endlich ist zo = oo ist ein entfernbarer singulärer Punkt der Funktion /(r). Wenn wir /(oo) = lim setzen J(z)= 0 also f(z) wird analytisch

Tic an der Stelle Zo= os. Lassen Sie uns zeigen, wie man die entsprechende Erweiterung (26.7) findet. Kommen wir zur Variablen w = 1 fz. Ersetzen z= 1 /?е, erhalten wir

(Die letzte Gleichung gilt in einer punktierten Umgebung des Punktes wо = 0, aber wir werden (7(0) = 0) weiter definieren. Die resultierende Funktion hat singuläre Punkte w =±i, w =-1/3 und auf den Punkt Wq = 0 ist analytisch. Entfaltungsfunktion G(w) nach und nach w(wie in Beispiel 25.7 durchgeführt) und Einsetzen in die resultierende Potenzreihe w = 1/z, können wir die Erweiterung (26.7) der Funktion erhalten f(z).

Satz 26.3 für den Fall zo= oo wird in der folgenden Form umgeschrieben.

Satz 26.12. Isolierter singulärer Punkt th = os Die Funktion f(z) ist genau dann ein Pol, wenn sie der Hauptteil der Laurent-Entwicklung ist (26.6) hat nur eine endliche Anzahl von Koeffizienten ungleich Null Mit":

Hier ist die Reihe der reguläre Teil und das Polynom in Klammern der Hauptteil der Entwicklung. Die Polmultiplizität in oc wird als Polmultiplizität definiert wq = 0 Funktionen G(z). Es ist leicht zu erkennen, dass die Multiplizität des Pols mit der Zahl übereinstimmt N in (26.8).

Q p | (i 2 + 1)(z+3) 2

Aufgabe. Zeigen Sie, dass die Funktion f(z) =-- -- hat in

Punkt zo = oo Pol der Ordnung 3.

Satz 26.6 über einen im Wesentlichen singulären Punkt kann für den Fall umgeschrieben werden zo= os fast wörtlich, und wir gehen nicht näher darauf ein.

Singularer Punkt

in Mathematik.

1) Sonderpunkt der Kurve, gegeben durch die Gleichung F ( x, y) = 0, - Punkt M 0 ( x 0 , y 0), in der beide partiellen Ableitungen der Funktion F ( x, y) auf Null gehen:

Wenn nicht alle zweiten partiellen Ableitungen der Funktion F ( x, y) am Punkt M 0 gleich Null sind, dann heißt das O. t. doppelt. Wenn neben den ersten Ableitungen im Punkt M0 auch alle zweiten Ableitungen verschwinden, aber nicht alle dritten Ableitungen, dann heißt die Gleichung Tripel usw. Bei der Untersuchung der Struktur einer Kurve in der Nähe eines doppelten O.t. spielt das Vorzeichen des Ausdrucks eine wichtige Rolle

Wenn Δ > 0, dann heißt der offene Raum isoliert; zum Beispiel an der Kurve y 2 - x 4 + 4x 2= 0 der Koordinatenursprung ist ein isoliertes O. t. (siehe. Reis. 1 ). Wenn Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - eine 4= 0 der Koordinatenursprung ist der Knoten O. t. (siehe. Reis. 2 ). Wenn Δ = 0, dann ist der allgemeine Punkt der Kurve entweder isoliert oder dadurch gekennzeichnet, dass verschiedene Äste der Kurve an diesem Punkt eine gemeinsame Tangente haben, zum Beispiel: a) Scheitelpunkt 1. Art – verschiedene Äste von Die Kurven liegen auf gegenüberliegenden Seiten der gemeinsamen Tangente und bilden einen Punkt, ähnlich einer Kurve y 2 - x 3= 0 (vgl Reis. 3 ,A); b) Scheitelpunkt 2. Art – verschiedene Äste der Kurve liegen wie eine Kurve auf einer Seite der gemeinsamen Tangente (y - x 2)2 - x 5= 0 (vgl Reis. 3 , B); c) Selbstberührungspunkt (für eine Kurve y 2 - x 4= 0 der Ursprung ist der Punkt der Selbstberührung; (cm. Reis. 3 , V). Neben dem angegebenen O. t. gibt es noch viele weitere O. t. mit besonderen Namen; Beispielsweise ist der asymptotische Punkt der Scheitelpunkt einer Spirale mit unendlich vielen Windungen (siehe. Reis. 4 ), Endpunkt, Eckpunkt usw.

2) Ein singulärer Punkt einer Differentialgleichung ist der Punkt, an dem sowohl der Zähler als auch der Nenner der rechten Seite der Differentialgleichung gleichzeitig verschwinden (siehe Differentialgleichungen).

wobei P und Q stetig differenzierbare Funktionen sind. Unter der Annahme, dass sich O. t. im Koordinatenursprung befindet, und unter Verwendung der Taylor-Formel (siehe Taylor-Formel) können wir Gleichung (1) in der Form darstellen

wo P 1 ( x, y) und Q 1 ( x, y) - infinitesimal in Bezug auf

Wenn nämlich λ 1 ≠ λ 2 und λ 1 λ 2 > 0 oder λ 1 = λ 2, dann ist das O. t. ein Knoten; Alle Integralkurven, die durch Punkte einer hinreichend kleinen Umgebung eines Knotens verlaufen, gehen in ihn ein. Wenn λ 1 ≠ λ 2 und λ 1 λ 2 i β, α ≠ 0 und β ≠ 0, dann ist der allgemeine Punkt ein Fokus; Alle Integralkurven, die durch Punkte in einer ausreichend kleinen Umgebung des Fokus verlaufen, stellen Spiralen mit unendlich vielen Windungen in jeder beliebig kleinen Umgebung des Fokus dar. Wenn schließlich λ 1,2 = ± ichβ, β ≠ 0, dann wird der Charakter des O. t. nicht allein durch lineare Terme in den Entwicklungen von P bestimmt ( x, y) und Q ( x, y), wie es in allen oben genannten Fällen der Fall war; hier kann O. t. ein Fokus oder Zentrum sein, oder es kann einen komplexeren Charakter haben. In der Nähe des Mittelpunkts sind alle Integralkurven geschlossen und enthalten den Mittelpunkt in sich. So ist beispielsweise der Punkt (0, 0) ein Knoten für die Gleichungen bei" = 2u/x(λ 1 = 1, λ 2 = 2; vgl Reis. 5 , a) und j" = u/x(λ 1 = λ 2 = 1; vgl Reis. 5 , b), Sattel für die Gleichung y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. Reis. 6 ), der Fokus für die Gleichung y" =(x + y) / (x - y) (λ 1 = 1 - ich, λ 2 = 1 + ich; cm. Reis. 7 ) und das Zentrum der Gleichung y" = -x/y(λ 1 = -ich, λ 2 = ich; cm. Reis. 8 ).

Wenn x, y) und Q ( x, y) analytisch, Nachbarschaft O. t. Auftrag von oben kann in Bereiche unterteilt werden: D 1 – gefüllt mit Integralkurven, beide Enden im O. t. enthalten (elliptische Bereiche), D 2 – gefüllt mit Integralkurven, ein Ende im O. t. enthalten (parabolische Bereiche), und D 3 - Regionen , begrenzt durch zwei in der allgemeinen Theorie enthaltene Integralkurven, zwischen denen Integralkurven vom Typ Hyperbel (hyperbolische Regionen) liegen (siehe Reis. 9 ). Wenn in einem allgemeinen Punkt keine Integralkurven enthalten sind, wird der allgemeine Punkt als Punkt stabilen Typs bezeichnet. Eine Umgebung eines stabilen Oszillators besteht aus geschlossenen Integralkurven, die in sich eine Osmose enthalten, zwischen denen sich Spiralen befinden (siehe Abb. Reis. 10 ).

Das Studium von Differentialgleichungen, also im Wesentlichen das Studium des Verhaltens von Familien von Integralkurven in der Umgebung von Differentialgleichungen, stellt einen Zweig der qualitativen Theorie der Differentialgleichungen dar und spielt in Anwendungen, insbesondere in Fragen der Bewegungsstabilität (Werke von A. M. Lyapunov, A. Poincaré usw.).

3) Ein singulärer Punkt einer einwertigen analytischen Funktion ist der Punkt, an dem die Analytizität der Funktion verletzt wird (siehe Analytische Funktionen). Wenn es eine Nachbarschaft von O. t. A, frei von anderen O. t., dann Punkt A genannt isoliert O. t. Wenn A- eine isolierte allgemeine Theorie und es existiert ein endliches a, wird als entfernbare allgemeine Theorie bezeichnet. Durch entsprechende Änderung der Definition einer Funktion an einem Punkt a (oder Neudefinition an diesem Punkt, wenn die Funktion an diesem Punkt überhaupt nicht definiert ist), nämlich durch Annahme F(A)= b, das ist möglich A wird zu einem gewöhnlichen Punkt der korrigierten Funktion. Zum Beispiel Punkt z= 0 ist ein abnehmbares O. t. für die Funktion f 1 ( z) = F(z), Wenn z≠ 0, und F 1 (0), = 1, Punkt z= 0 ist ein gewöhnlicher Punkt [ F 1 (z) ist in diesem Punkt analytisch z= 0]. Wenn A- ein isoliertes O. t. und a heißt Pol oder unwesentlich singulärer Punkt einer Funktion F(z), wenn die Laurent-Reihe funktioniert F(z) in der Nähe eines isolierten O. t. enthält keine negativen Kräfte z - a, Wenn A- abnehmbares O. t., enthält eine endliche Anzahl negativer Grade z - a, Wenn A- Pol (in diesem Fall die Reihenfolge des Pols R ist definiert als der höchste Grad von a – ein im Wesentlichen besonderer Punkt. Zum Beispiel für die Funktion

p = 2, 3, …)

Punkt z= 0 ist der Pol der Ordnung R, für Funktion

Punkt z= 0 ist ein im Wesentlichen singulärer Punkt.

Auf dem Rand des Konvergenzkreises einer Potenzreihe muss mindestens ein DP der Funktion liegen, die innerhalb dieses Kreises durch die gegebene Potenzreihe repräsentiert wird. Alle Randpunkte des Existenzbereichs einer eindeutigen analytischen Funktion (natürliche Grenze) sind die Grenzen dieser Funktion. Somit sind alle Punkte des Einheitskreises | z| = 1 sind speziell für die Funktion

Für eine mehrwertige analytische Funktion ist das Konzept von „O. T." schwieriger. Zusätzlich zum O. t. ist in einzelnen Blättern der Riemannschen Oberfläche einer Funktion (d. h. dem O. t. einwertiger analytischer Elemente) jeder Verzweigungspunkt auch der O. t. der Funktion. Isolierte Verzweigungspunkte einer Riemannschen Oberfläche (d. h. solche Verzweigungspunkte, bei denen es in ihrer Nachbarschaft keine anderen O. t.-Funktionen in irgendeinem Blatt gibt) werden wie folgt klassifiziert. Wenn a ein isolierter Verzweigungspunkt endlicher Ordnung ist und es ein endliches a gibt, spricht man von einem kritischen Pol. Wenn A- ein isolierter Verzweigungspunkt unendlicher Ordnung und a heißt transzendentales O.t. Alle anderen isolierten Verzweigungspunkte werden kritische, im Wesentlichen singuläre Punkte genannt. Beispiele: Punkt z= 0 ist gewöhnlich kritischer Punkt Funktionen f ( z) = log z und der kritische, im Wesentlichen singuläre Punkt der Funktion F (z) = sin ln z.

Jede allgemeine Theorie, außer einer entfernbaren, stellt ein Hindernis für die analytische Fortsetzung dar, das heißt, eine analytische Fortsetzung entlang einer Kurve, die durch ein irreduzibles allgemeines Problem verläuft, ist unmöglich.

Groß Sowjetische Enzyklopädie. - M.: Sowjetische Enzyklopädie. 1969-1978 .

Sehen Sie in anderen Wörterbüchern, was ein „Singular Point“ ist:

Punkte hier. Siehe auch Singularpunkt ( Differentialgleichung). Ein Merkmal oder eine Singularität ist in der Mathematik ein Punkt, an dem ein mathematisches Objekt (normalerweise eine Funktion) undefiniert ist oder ein unregelmäßiges Verhalten aufweist (zum Beispiel ein Punkt, an dem ... ... Wikipedia

Eine analytische Funktion ist ein Punkt, an dem die Bedingungen der Analytizität verletzt werden. Wenn die analytische Funktion f(z) überall in einer bestimmten Umgebung des Punktes z0 gegeben ist ... Physische Enzyklopädie

Eine analytische Funktion ist der Punkt, an dem die Analytizität der Funktion verletzt wird ... Großes enzyklopädisches Wörterbuch

singulärer Punkt- - [Ya.N.Luginsky, M.S.Fezi Zhilinskaya, Yu.S.Kabirov. Englisch-Russisches Wörterbuch der Elektrotechnik und Energietechnik, Moskau, 1999] Themen der Elektrotechnik, Grundkonzepte EN Singularpunkt ... Leitfaden für technische Übersetzer

1) Eine analytische Funktion f(z) ist ein Hindernis für die analytische Fortsetzung eines Elements einer Funktion f(z) einer komplexen Variablen z entlang eines Pfades auf der Ebene dieser Variablen. Die analytische Funktion f(z) sei definiert durch einige... ... Mathematische Enzyklopädie

Analytische Funktion, der Punkt, an dem die Analytizität der Funktion verletzt wird. * * * EINZELNER PUNKT EINZELNER PUNKT einer analytischen Funktion, der Punkt, an dem die Analytizität der Funktion verletzt wird... Enzyklopädisches Wörterbuch

singulärer Punkt- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. singulärer Punktvok. singulärer Punkt, m rus. Singularpunkt, f pranc. point particulier, m; point singulier, m … Automatikos terminų žodynas

singulärer Punkt- ypatingasis taškas statusas T sritis fizika atitikmenys: engl. singulärer Punktvok. singulärer Punkt, m rus. Singularpunkt, f pranc. point singulier, m … Fizikos terminų žodynas