Zentralmomentformel vierter Ordnung. Erste und zentrale theoretische Punkte

3.4. Momente einer Zufallsvariablen.

Oben haben wir die umfassenden Eigenschaften des SV kennengelernt: die Verteilungsfunktion und die Verteilungsreihe für ein diskretes SV, die Verteilungsfunktion und Wahrscheinlichkeitsdichte für ein kontinuierliches SV. Diese paarweise äquivalenten Merkmale hinsichtlich des Informationsgehalts sind Funktionen und beschreiben Sie den SV aus probabilistischer Sicht vollständig. In vielen praktischen Situationen ist es jedoch entweder unmöglich oder unnötig, eine Zufallsvariable umfassend zu charakterisieren. Oft reicht es aus, eine oder mehrere anzugeben numerisch Parameter, die bis zu einem gewissen Grad die Hauptmerkmale der Verteilung beschreiben, und manchmal ist das Finden umfassender Merkmale mathematisch zwar wünschenswert, aber zu schwierig, und wenn wir mit numerischen Parametern arbeiten, sind wir auf eine ungefähre, aber einfachere Beschreibung beschränkt. Die angegebenen numerischen Parameter werden aufgerufen numerische Merkmale Zufallsvariable und Spiel große Rolle in der Anwendung der Wahrscheinlichkeitstheorie auf verschiedene Bereiche der Wissenschaft und Technologie, um die Lösung von Problemen zu erleichtern und die Darstellung der Lösungsergebnisse in einer einfachen und visuellen Form zu ermöglichen.

Die am häufigsten verwendeten numerischen Merkmale können in zwei Typen unterteilt werden: Momente und Positionsmerkmale. Es gibt verschiedene Arten von Momenten, von denen die beiden am häufigsten verwendeten sind: primär und zentral. Andere Arten von Momenten, z.B. absolute Momente, faktorielle Momente, berücksichtigen wir nicht. Um die Verwendung einer Verallgemeinerung des Integrals – des sogenannten Stieltjes-Integrals – zu vermeiden, werden wir Definitionen von Momenten getrennt für kontinuierliche und diskrete SVs angeben.

Definitionen. 1. Der StartmomentkDiskreter SV der -ten Ordnung heißt Menge

Wo F(X) ist die Wahrscheinlichkeitsdichte eines gegebenen SV.

3. Zentraler MomentkDiskreter SV der -ten Ordnung heißt Menge

In Fällen, in denen mehrere SVs gleichzeitig in Betracht gezogen werden, ist es zur Vermeidung von Missverständnissen zweckmäßig, die Identität des Augenblicks anzugeben; Wir tun dies, indem wir in Klammern die Bezeichnung des entsprechenden SV angeben, z. B. usw. Diese Bezeichnung sollte nicht mit der Funktionsnotation verwechselt werden, und der Buchstabe in Klammern sollte nicht mit dem Funktionsargument verwechselt werden. Summen und Integrale auf der rechten Seite von Gleichungen (3.4.1 - 3.4.4) können je nach Wert konvergieren oder divergieren k und spezifische Verteilung. Im ersten Fall sagen sie, dass der Moment existiert nicht oder weicht ab, im zweiten - was Moment existiert oder konvergiert. Wenn ein diskreter SV eine endliche Anzahl endlicher Werte hat ( N natürlich), dann sind alle seine Momente von endlicher Ordnung k existieren. Im Unendlichen N, ausgehend von einigen k und für höhere Ordnungen existieren die Momente eines diskreten SV (sowohl Anfangs- als auch Zentralmomente) möglicherweise nicht. Die Momente eines stetigen SV werden, wie aus den Definitionen hervorgeht, durch unechte Integrale ausgedrückt, die ab einem bestimmten Wert divergieren können k und für höhere Ordnungen (gleichzeitig initial und zentral). Momente nullter Ordnung konvergieren immer.

Betrachten wir zunächst die anfänglichen und dann die zentralen Momente genauer. Aus mathematischer Sicht der Anfangsmoment k-te Ordnung ist der „gewichtete Durchschnitt“ k-ter Grad der SV-Werte; Im Fall eines diskreten SV sind die Gewichte die Wahrscheinlichkeiten von Werten; im Fall eines kontinuierlichen SV ist die Gewichtsfunktion die Wahrscheinlichkeitsdichte. Operationen dieser Art werden in der Mechanik häufig zur Beschreibung der Massenverteilung (statische Momente, Trägheitsmomente usw.) verwendet; Die sich dabei ergebenden Analogien werden im Folgenden erörtert.

Zum besseren Verständnis der Anfangsmomente betrachten wir diese gesondert als gegeben k. In der Wahrscheinlichkeitstheorie sind die Momente niedrigerer Ordnung am wichtigsten, also klein k Daher sollte die Betrachtung in der Reihenfolge steigender Werte erfolgen k. Das Anfangsmoment nullter Ordnung ist gleich

1, für diskrete SV;

=1, für kontinuierliches SV,

diese. für jedes SV ist es gleich dem gleichen Wert – eins, und enthält daher keine Informationen über die statistischen Eigenschaften des SV.

Das Anfangsmoment erster Ordnung (oder erstes Anfangsmoment) ist gleich

Für diskrete SV;

, für kontinuierliche SV.

Dieser Punkt ist das wichtigste numerische Merkmal eines jeden SV, wofür es mehrere miteinander verbundene Gründe gibt. Erstens tendiert nach dem Satz von Tschebyschew (siehe Abschnitt 7.4) bei einer unbegrenzten Anzahl von Tests zum SV das arithmetische Mittel der beobachteten Werte (gewissermaßen) zu , also ist dies für jeden SV eine charakteristische Zahl um die sich seine Werte nach Erfahrung gruppieren. Zweitens ist es für einen kontinuierlichen Lebenslauf numerisch gleich X-te Koordinate des Schwerpunkts des durch die Kurve gebildeten krummlinigen Trapezes F(X) (eine ähnliche Eigenschaft tritt für ein diskretes SV auf), daher könnte dieser Moment als „Schwerpunkt der Verteilung“ bezeichnet werden. Drittens verfügt dieses Moment über bemerkenswerte mathematische Eigenschaften, die insbesondere im Laufe des Kurses deutlich werden, weshalb sein Wert in den Ausdrücken für zentrale Momente enthalten ist (siehe (3.4.3) und (3.4.4)).

Die Bedeutung dieses Moments für theoretische und praktische Probleme der Wahrscheinlichkeitstheorie und seine bemerkenswerten mathematischen Eigenschaften haben dazu geführt, dass in der Literatur neben der Bezeichnung und dem Namen „erster Anfangsmoment“ mehr oder weniger auch andere Bezeichnungen und Namen verwendet werden praktisch und spiegelt die genannten Eigenschaften wider. Die gebräuchlichsten Namen sind: erwarteter Wert, mittlere Bedeutung, und Notation: M, M[X], . Am häufigsten verwenden wir den Begriff „mathematische Erwartung“ und die Notation M; Wenn es mehrere SVs gibt, verwenden wir einen Index, der die Identität der mathematischen Erwartung angibt, zum Beispiel: M X , M j usw.

Das Anfangsmoment zweiter Ordnung (oder zweites Anfangsmoment) ist gleich

Für diskrete SV;

, für kontinuierliches SV;

manchmal heißt es mittleres Quadrat der Zufallsvariablen und ist bezeichnet M.

Das Anfangsmoment dritter Ordnung (oder drittes Anfangsmoment) ist gleich

Für diskrete SV;

, für kontinuierlichen CB

manchmal heißt es durchschnittlicher Würfel einer Zufallsvariablen und ist bezeichnet M[X 3 ].

Es hat keinen Sinn, weiterhin die Ausgangspunkte aufzuzählen. Bleiben wir bei der wichtigen Interpretation von Ordnungsmomenten k>1. Lassen Sie zusammen mit SV X es gibt auch einen SV Y, Und Y=X k (k=2, 3, ...). Diese Gleichheit bedeutet, dass die Zufallsvariablen X Und Y sind deterministisch in dem Sinne verbunden, dass wenn SV X nimmt den Wert an X, NE Y nimmt den Wert an y=x k(In Zukunft wird dieser Zusammenhang von SV genauer betrachtet). Dann ist nach (3.4.1) und (3.4.2)

=M j , k=2, 3, ...,

d.h. k Das Anfangsmoment von SV entspricht dem mathematischen Erwartungswert k-te Potenz dieser Zufallsvariablen. Beispielsweise ist das dritte Anfangsmoment der Kantenlänge eines zufälligen Würfels gleich dem mathematischen Erwartungswert des Würfelvolumens. Die Fähigkeit, Momente als sicher zu begreifen mathematische Erwartungen- ein weiterer Aspekt der Bedeutung des Konzepts der mathematischen Erwartung.

Kommen wir nun zu den zentralen Punkten. Da, wie im Folgenden noch deutlich wird, zentrale Momente eindeutig durch Initialmomente zum Ausdruck kommen und umgekehrt, stellt sich die Frage, warum es Zentralmomente überhaupt braucht und warum Initialmomente nicht ausreichen. Betrachten wir SV X(kontinuierlich oder diskret) und ein weiteres SV Y, bezogen auf das erste als Y=X+a, Wo A 0 ist eine nicht zufällige reelle Zahl. Jeder Wert X zufällige Variable X entspricht dem Wert y=x+a zufällige Variable Y, daher die Verteilung von SV Y wird die gleiche Form haben (ausgedrückt durch das Verteilungspolygon im diskreten Fall oder die Wahrscheinlichkeitsdichte - in kontinuierlicher Fall), das gleiche wie die Verteilung von SV X, jedoch entlang der x-Achse um den Betrag verschoben A. Folglich sind die Anfangsmomente von SV Y wird von den entsprechenden Momenten von SV abweichen X. Es ist zum Beispiel leicht zu erkennen M j =m X +a(Momente mehr hoher Auftrag durch komplexere Zusammenhänge verbunden sind). Das haben wir also festgestellt Die Anfangsmomente sind in Bezug auf die Verschiebung der Verteilung als Ganzes nicht invariant. Das gleiche Ergebnis erhält man, wenn man nicht die Verteilung, sondern den Anfang der x-Achse horizontal um einen Betrag verschiebt - A, d.h. Die entsprechende Schlussfolgerung gilt auch: Die Anfangsmomente sind nicht invariant in Bezug auf die horizontale Verschiebung des Anfangs der x-Achse.

Zentrale Momente, die die Eigenschaften von Verteilungen beschreiben sollen, die nicht von ihrer Verschiebung als Ganzes abhängen, weisen diesen Nachteil nicht auf. In der Tat, wie aus (3.4.3) und (3.4.4) ersichtlich ist, wenn sich die Verteilung als Ganzes um einen Betrag verschiebt A, oder, was dasselbe ist, den Anfang der x-Achse um den Betrag verschieben - A, alle Werte X, mit den gleichen Wahrscheinlichkeiten (im diskreten Fall) oder der gleichen Wahrscheinlichkeitsdichte (im kontinuierlichen Fall), wird sich um den Betrag ändern A, aber die Menge ändert sich um den gleichen Betrag M, sodass sich die Werte der Klammern auf der rechten Seite der Gleichungen nicht ändern. Auf diese Weise, Die zentralen Momente sind invariant gegenüber der Verschiebung der Verteilung als Ganzes oder, was dasselbe ist, gegenüber der horizontalen Verschiebung des Anfangs der x-Achse. Den Namen „zentral“ erhielten diese Momente damals, als der erste Anfangsmoment „Zentrum“ genannt wurde. Es ist nützlich zu beachten, dass der zentrale Moment von SV X kann als das entsprechende Anfangsmoment von SV verstanden werden X 0 gleich

X 0 =X-m X .

NE X 0 heißt zentriert(bezogen auf SV X) und die dazu führende Operation, d. h. das Subtrahieren ihres mathematischen Erwartungswerts von einer Zufallsvariablen, wird aufgerufen Zentrierung. Wie wir später sehen werden, werden dieses Konzept und diese Operation im gesamten Kurs nützlich sein. Beachten Sie, dass das zentrale Moment der Ordnung ist k>1 kann als mathematische Erwartung (Durchschnitt) angesehen werden k-ter Grad des zentrierten SV: .

Betrachten wir getrennt die zentralen Momente der unteren Ordnungen. Das zentrale Moment nullter Ordnung ist gleich

, für diskrete SVs;

, für kontinuierliches SV;

d.h. für jedes SV und enthält keine Informationen über die statistischen Eigenschaften dieses SV.

Das Zentralmoment erster Ordnung (oder erstes Zentralmoment) ist gleich

für diskrete SV;

für Dauer-CB; d.h. für jedes SV und enthält keine Informationen über die statistischen Eigenschaften dieses SV.

Das zentrale Moment zweiter Ordnung (oder zweites zentrales Moment) ist gleich

, für diskrete SV;

, für kontinuierliche SV.

Wie weiter unten deutlich wird, ist dieser Punkt einer der wichtigsten in der Wahrscheinlichkeitstheorie, da er als Merkmal des Maßes für die Streuung (oder Streuung) von SV-Werten verwendet wird und daher oft als „Dispersion“ bezeichnet wird Streuung und ist bezeichnet D X. Beachten Sie, dass dies als mittleres Quadrat des zentrierten SV verstanden werden kann.

Das Zentralmoment dritter Ordnung (dritte Zentralmoment) ist gleich

Erwarteter Wert. Mathematische Erwartung diskrete Zufallsvariable X, wobei eine endliche Anzahl von Werten angenommen wird Xich mit Wahrscheinlichkeiten Rich, der Betrag heißt:

Mathematische Erwartung kontinuierliche Zufallsvariable X heißt das Integral des Produkts seiner Werte X auf der WahrF(X):

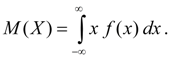(6B)

Uneigentliches Integral (6 B) wird als absolut konvergent angenommen (andernfalls sagt man, dass die mathematische Erwartung M(X) existiert nicht). Die mathematische Erwartung charakterisiert mittlere Bedeutung zufällige Variable X. Seine Dimension stimmt mit der Dimension der Zufallsvariablen überein.

Eigenschaften der mathematischen Erwartung:

Streuung. Varianz zufällige Variable X die Nummer heißt:

Die Varianz ist Streucharakteristik Zufallsvariablenwerte X relativ zu seinem Durchschnittswert M(X). Die Varianzdimension ist gleich der Dimension der Zufallsvariablen im Quadrat. Basierend auf den Definitionen der Varianz (8) und des mathematischen Erwartungswerts (5) für eine diskrete Zufallsvariable und (6) für eine kontinuierliche Zufallsvariable erhalten wir ähnliche Ausdrücke für die Varianz:

(9)

Hier M = M(X).

Dispersionseigenschaften:

Standardabweichung:

(11)

Da die Standardabweichung die gleiche Dimension wie eine Zufallsvariable hat, wird sie häufiger als Maß für die Streuung als für die Varianz verwendet.

Momente der Verteilung. Die Konzepte des mathematischen Erwartungswerts und der Streuung sind Sonderfälle von mehr allgemeines Konzept für numerische Merkmale zufällige Variablen – Verteilungsmomente. Die Verteilungsmomente einer Zufallsvariablen werden als mathematische Erwartungen einiger einfacher Funktionen einer Zufallsvariablen eingeführt. Also, Moment der Ordnung k relativ zum Punkt X 0 wird als mathematischer Erwartungswert bezeichnet M(X–X 0 )k. Momente über den Ursprung X= 0 aufgerufen werden erste Momente und werden bezeichnet:

(12)

Das Anfangsmoment erster Ordnung ist das Zentrum der Verteilung der betrachteten Zufallsvariablen:

(13)

Momente über das Verteilungszentrum X= M werden genannt zentrale Punkte und werden bezeichnet:

(14)

Aus (7) folgt, dass das Zentralmoment erster Ordnung immer ist gleich Null:

Die zentralen Momente hängen nicht vom Ursprung der Werte der Zufallsvariablen ab, da sie um einen konstanten Wert verschoben werden MIT sein Verteilzentrum verschiebt sich um den gleichen Wert MIT, und die Abweichung vom Zentrum ändert sich nicht: X – M = (X – MIT) – (M – MIT).
Jetzt ist es offensichtlich Streuung- Das Zentralmoment zweiter Ordnung:

Asymmetrie. Zentrales Moment dritter Ordnung:

(17)

dient der Auswertung Verteilungsasymmetrien. Wenn die Verteilung symmetrisch zum Punkt ist X= M, dann ist das Zentralmoment dritter Ordnung gleich Null (wie alle Zentralmomente ungerader Ordnung). Wenn also das Zentralmoment dritter Ordnung von Null verschieden ist, kann die Verteilung nicht symmetrisch sein. Das Ausmaß der Asymmetrie wird dimensionslos beurteilt Asymmetriekoeffizient:

(18)

Das Vorzeichen des Asymmetriekoeffizienten (18) zeigt eine rechtsseitige oder linksseitige Asymmetrie an (Abb. 2).

Reis. 2. Arten der Verteilungsasymmetrie.

Überschuss. Zentrales Moment vierter Ordnung:

(19)

dient der Auswertung der sogenannten Überschuss, der den Grad der Steilheit (Spitze) der Verteilungskurve nahe der Mitte der Verteilung im Verhältnis zur Normalverteilungskurve bestimmt. Da für eine Normalverteilung der als Kurtosis angenommene Wert ist:

(20)

In Abb. 3 zeigt Beispiele für Verteilungskurven mit unterschiedliche BedeutungenÜberschuss. Für Normalverteilung E= 0. Kurven, die spitzer als normal sind, haben eine positive Kurtosis, Kurven mit flacheren Spitzen haben eine negative Kurtosis.

Reis. 3. Verteilungskurven mit unterschiedlicher Steilheit (Kurtosis).

Momente höherer Ordnung in technischen Anwendungen mathematische Statistik normalerweise nicht verwendet.

Mode diskret Eine Zufallsvariable ist ihr wahrscheinlichster Wert. Mode kontinuierlich Eine Zufallsvariable ist ihr Wert, bei dem die Wahrscheinlichkeitsdichte maximal ist (Abb. 2). Wenn die Verteilungskurve ein Maximum hat, wird die Verteilung aufgerufen unimodal. Wenn eine Verteilungskurve mehr als ein Maximum aufweist, wird die Verteilung aufgerufen multimodal. Manchmal gibt es Verteilungen, deren Kurven ein Minimum anstelle eines Maximums aufweisen. Solche Verteilungen heißen antimodal. Im allgemeinen Fall stimmen Modus und mathematische Erwartung einer Zufallsvariablen nicht überein. Im Sonderfall, z modal, d.h. eine modussymmetrische Verteilung aufweist und sofern eine mathematische Erwartung vorliegt, stimmt diese mit dem Modus und dem Symmetriezentrum der Verteilung überein.

Median zufällige Variable X- das ist seine Bedeutung Meh, für die Gleichheit gilt: d.h. es ist ebenso wahrscheinlich, dass die Zufallsvariable X wird weniger oder mehr sein Meh. Geometrisch Median ist die Abszisse des Punktes, an dem die Fläche unter der Verteilungskurve in zwei Hälften geteilt wird (Abb. 2). Bei einer symmetrischen Modalverteilung sind Median, Modus und mathematischer Erwartungswert gleich.

Offensichtlich ist das anfängliche Abtastmoment nullter Ordnung immer gleich 1 und das anfängliche Abtastmoment erster Ordnung

Definition 2.19 Zentralmoment k - erster BemusterungsauftragX 1 , X 2 , …, X Nwird als Durchschnitt der k-ten Abweichungsgrade der Datenprobenwerte vom Durchschnitt bezeichnet

Aus diese Definition Daraus folgt, dass das zentrale Abtastmoment nullter Ordnung gleich 1 ist. Für k = 1 stellt sich heraus, dass

, und für k= 2 gilt

.

Daher ist die Stichprobenvarianz ein zentrales Stichprobenmoment zweiter Ordnung. Um das zentrale Stichprobenmoment dritter Ordnung zu berechnen, verwenden wir standardmäßige algebraische Transformationen:

Das Ergebnis war ein Ausdruck des zentralen Moments dritter Ordnung in Bezug auf die Anfangsmomente. Auf die gleiche Weise findet man Ausdrücke für Zentralmomente höherer Ordnung. Hier sind einige Formeln, die in der Praxis häufiger verwendet werden als andere:

Bei der Berechnung der anfänglichen und zentralen Stichprobenzeitpunkte werden Techniken und Tabellen verwendet, die denen ähneln, die zuvor zur Berechnung des Mittelwerts und der Varianz verwendet wurden.

Beispiel 2.28 Die soziologische Studie sammelte Antworten von 25 einfachen Mitarbeitern der Einrichtung über die Anzahl der Stresssituationen, die während der Woche am Arbeitsplatz auftraten. Die Umfragedaten sind in der folgenden Tabelle aufgeführt. Lassen Sie uns die anfänglichen und zentralen Beispielmomente erster, zweiter, dritter und vierter Ordnung finden.

Tabelle 2.20– Daten aus einer Studie zu Stresssituationen

Die notwendigen Zwischenberechnungen werden wir in der folgenden Tabelle festhalten.

Tabelle 2.21 – Berechnung von Anfangs- und Zentralmomenten

Stichprobengröße n = 25. Berechnen wir die anfänglichen Stichprobenmomente:

; ;

; .

Mit den entsprechenden Formeln berechnen wir die zentralen Stichprobenmomente:

Runden wir die erhaltenen Werte der Zentralmomente ab:

; ; ;

Anfängliche und zentrale Stichprobenmomente sind Analoga der entsprechenden Konzepte theoretischer Momente der gesamten Gesamtpopulation von Werten der untersuchten Zufallsvariablen.

Definition 2.20 AnfangsmomentkDie te Ordnung einer Zufallsvariablen X ist eine Zahl, die dem mathematischen Erwartungswert entsprichtk-ter Grad der Größe X:

.

Zur Berechnung des Anfangsmoments der k-ten Ordnung werden folgende Formeln verwendet:

Es ist offensichtlich, dass der mathematische Erwartungswert einer Zufallsvariablen das Anfangsmoment erster Ordnung und die Varianz das Zentralmoment zweiter Ordnung ist. Bei der Untersuchung des Verteilungsgesetzes einer Zufallsvariablen werden sowohl theoretische als auch Stichprobenmomente verwendet. Alle zentralen Momente gerader Ordnung sowie die Streuung charakterisieren die Streuung der Werte einer Zufallsvariablen um den mathematischen Erwartungswert. Zentrale Momente ungerader Ordnung offenbaren die Asymmetrie der Verteilung relativ zum Zentrum. Insbesondere wenn die Werte einer Zufallsvariablen symmetrisch bezüglich des mathematischen Erwartungswerts verteilt sind, dann sind alle ihre vorhandenen Momente ungerader Ordnung gleich Null. Andererseits weist die Existenz eines Zentralmoments ungerader Ordnung ungleich Null auf das Vorhandensein einer Verteilungsasymmetrie hin.

Neben Positionsmerkmalen – durchschnittlichen, typischen Werten einer Zufallsvariablen – werden eine Reihe von Merkmalen verwendet, die jeweils die eine oder andere Eigenschaft der Verteilung beschreiben. Als solche Merkmale werden am häufigsten die sogenannten Momente verwendet.

Der Begriff des Moments wird in der Mechanik häufig zur Beschreibung der Massenverteilung (statische Momente, Trägheitsmomente usw.) verwendet. Genau die gleichen Techniken werden in der Wahrscheinlichkeitstheorie verwendet, um die grundlegenden Eigenschaften der Verteilung einer Zufallsvariablen zu beschreiben. Am häufigsten werden in der Praxis zwei Arten von Momenten verwendet: anfängliche und zentrale.

Das Anfangsmoment etw. Ordnung einer diskontinuierlichen Zufallsvariablen ist eine Summe der Form:

. (5.7.1)

Offensichtlich stimmt diese Definition mit der Definition des Anfangsmoments der Ordnung s in der Mechanik überein, wenn Massen auf der Abszissenachse in Punkten konzentriert sind.

Für eine kontinuierliche Zufallsvariable X wird das Anfangsmoment etw. Ordnung als Integral bezeichnet

. (5.7.2)

Es ist leicht zu erkennen, dass das Hauptmerkmal der in der vorherigen Nr. eingeführten Position – die mathematische Erwartung – nichts anderes als das erste Anfangsmoment der Zufallsvariablen ist.

Mithilfe des mathematischen Erwartungszeichens können Sie zwei Formeln (5.7.1) und (5.7.2) zu einer kombinieren. Tatsächlich sind die Formeln (5.7.1) und (5.7.2) in ihrer Struktur den Formeln (5.6.1) und (5.6.2) völlig ähnlich, mit dem Unterschied, dass anstelle von und jeweils und stehen. Daher können wir eine allgemeine Definition des Anfangsmoments der Ordnung schreiben, die sowohl für diskontinuierliche als auch für kontinuierliche Größen gilt:

, (5.7.3)

diese. Der Anfangszeitpunkt der Ordnung einer Zufallsvariablen ist der mathematische Erwartungswert des Grades dieser Zufallsvariablen.

Bevor wir das zentrale Moment definieren, führen wir ein neues Konzept der „zentrierten Zufallsvariablen“ ein.

Es sei eine Zufallsvariable mit mathematischem Erwartungswert. Eine dem Wert entsprechende zentrierte Zufallsvariable ist die Abweichung der Zufallsvariablen von ihrer mathematischen Erwartung:

In Zukunft werden wir uns darauf einigen, die zentrierte Zufallsvariable, die einer gegebenen Zufallsvariablen entspricht, überall mit demselben Buchstaben und einem Symbol oben zu bezeichnen.

Es lässt sich leicht überprüfen, dass der mathematische Erwartungswert einer zentrierten Zufallsvariablen gleich Null ist. Tatsächlich für eine diskontinuierliche Menge

ähnlich für eine kontinuierliche Menge.

Das Zentrieren einer Zufallsvariablen ist offensichtlich gleichbedeutend mit dem Verschieben des Koordinatenursprungs zum mittleren, „zentralen“ Punkt, dessen Abszisse dem mathematischen Erwartungswert entspricht.

Die Momente einer zentrierten Zufallsvariablen werden Zentralmomente genannt. Sie sind analog zu Momenten um den Schwerpunkt in der Mechanik.

Somit ist das zentrale Ordnungsmoment s einer Zufallsvariablen der mathematische Erwartungswert der Potenz der entsprechenden zentrierten Zufallsvariablen:

, (5.7.6)

und für stetig – durch das Integral

. (5.7.8)

Im Folgenden werden wir in Fällen, in denen kein Zweifel darüber besteht, zu welcher Zufallsvariablen ein bestimmter Moment gehört, der Kürze halber einfach und anstelle von und schreiben.

Offensichtlich ist für jede Zufallsvariable das Zentralmoment erster Ordnung gleich Null:

, (5.7.9)

da der mathematische Erwartungswert einer zentrierten Zufallsvariablen immer gleich Null ist.

Lassen Sie uns Beziehungen ableiten, die die zentralen und anfänglichen Momente verschiedener Ordnungen verbinden. Wir werden die Schlussfolgerung nur für diskontinuierliche Mengen durchführen; Es lässt sich leicht überprüfen, dass genau die gleichen Beziehungen für kontinuierliche Größen gelten, wenn wir endliche Summen durch Integrale und Wahrscheinlichkeiten durch Wahrscheinlichkeitselemente ersetzen.

Betrachten wir den zweiten zentralen Punkt:

Ebenso erhalten wir für das dritte zentrale Moment:

Ausdrücke für usw. können auf ähnliche Weise erhalten werden.

Somit gelten für die zentralen Momente jeder Zufallsvariablen die Formeln:

(5.7.10)

Im Allgemeinen können Momente nicht nur relativ zum Ursprung (Anfangsmomente) oder zur mathematischen Erwartung (Zentralmomente) betrachtet werden, sondern auch relativ zu einem beliebigen Punkt:

. (5.7.11)

Allerdings haben Zentralmomente einen Vorteil gegenüber allen anderen: Das erste Zentralmoment ist, wie wir gesehen haben, immer gleich Null, und das nächste, das zweite Zentralmoment, hat bei diesem Bezugssystem einen Minimalwert. Lass es uns beweisen. Für eine diskontinuierliche Zufallsvariable at hat die Formel (5.7.11) die Form:

. (5.7.12)

Lassen Sie uns diesen Ausdruck umwandeln:

Offensichtlich erreicht dieser Wert sein Minimum, wenn , d. h. wenn der Moment relativ zum Punkt genommen wird.

Von allen Momenten werden das erste Anfangsmoment (mathematische Erwartung) und das zweite Zentralmoment am häufigsten als Merkmale einer Zufallsvariablen verwendet.

Das zweite zentrale Moment wird als Varianz der Zufallsvariablen bezeichnet. Aufgrund der außerordentlichen Bedeutung dieses Merkmals führen wir unter anderem eine besondere Bezeichnung dafür ein:

Nach der Definition des zentralen Moments

diese. Die Varianz einer Zufallsvariablen X ist der mathematische Erwartungswert des Quadrats der entsprechenden zentrierten Variablen.

Wenn wir die Menge im Ausdruck (5.7.13) durch ihren Ausdruck ersetzen, erhalten wir auch:

. (5.7.14)

Um die Varianz direkt zu berechnen, verwenden Sie die folgenden Formeln:

, (5.7.15)

(5.7.16)

Entsprechend für diskontinuierliche und kontinuierliche Mengen.

Die Streuung einer Zufallsvariablen ist ein Merkmal der Streuung, der Streuung der Werte einer Zufallsvariablen um ihren mathematischen Erwartungswert. Das Wort „Dispersion“ selbst bedeutet „Streuung“.

Wenden wir uns der mechanischen Interpretation der Verteilung zu, dann ist die Streuung nichts anderes als das Trägheitsmoment einer gegebenen Massenverteilung relativ zum Schwerpunkt (mathematische Erwartung).

Die Varianz einer Zufallsvariablen hat die Dimension des Quadrats der Zufallsvariablen; Um die Streuung visuell zu charakterisieren, ist es bequemer, eine Größe zu verwenden, deren Dimension mit der Dimension der Zufallsvariablen übereinstimmt. Ziehen Sie dazu die Quadratwurzel aus der Varianz. Der resultierende Wert wird als Standardabweichung (sonst „Standard“) der Zufallsvariablen bezeichnet. Wir bezeichnen die Standardabweichung als:

, (5.7.17)

Um die Schreibweise zu vereinfachen, verwenden wir häufig die Abkürzungen für Standardabweichung und Streuung: und . Wenn kein Zweifel besteht, auf welche Zufallsvariable sich diese Merkmale beziehen, lassen wir manchmal das Symbol x y und weg und schreiben einfach und . Die Wörter „Standardabweichung“ werden manchmal abgekürzt und durch die Buchstaben r.s.o. ersetzt.

In der Praxis wird häufig eine Formel verwendet, die die Streuung einer Zufallsvariablen durch ihr zweites Anfangsmoment (das zweite der Formeln (5.7.10)) ausdrückt. In der neuen Notation wird es so aussehen:

Erwartungswert und Varianz (oder Standardabweichung) sind die am häufigsten verwendeten Merkmale einer Zufallsvariablen. Sie charakterisieren die wichtigsten Merkmale der Verteilung: ihre Position und den Grad der Streuung. Zur detaillierteren Beschreibung der Verteilung werden Momente höherer Ordnung verwendet.

Der dritte zentrale Punkt dient zur Charakterisierung der Asymmetrie (oder „Schiefe“) der Verteilung. Wenn die Verteilung symmetrisch in Bezug auf die mathematische Erwartung ist (oder, in einer mechanischen Interpretation, die Masse symmetrisch in Bezug auf den Schwerpunkt verteilt ist), dann sind alle Momente ungerader Ordnung (falls vorhanden) gleich Null. Tatsächlich, insgesamt

Wenn das Verteilungsgesetz symmetrisch und ungerade ist, entspricht jeder positive Term einem negativen Term mit gleichem Absolutwert, sodass die gesamte Summe gleich Null ist. Das Gleiche gilt offensichtlich auch für das Integral

,

die als Integral in den symmetrischen Grenzen einer ungeraden Funktion gleich Null ist.

Es liegt daher nahe, eines der ungeraden Momente als Merkmal der Verteilungsasymmetrie zu wählen. Das einfachste davon ist das dritte zentrale Moment. Es hat die Dimension der dritten Potenz einer Zufallsvariablen: Um ein dimensionsloses Merkmal zu erhalten, wird das dritte Moment durch die Potenz der Standardabweichung dividiert. Der resultierende Wert wird „Asymmetriekoeffizient“ oder einfach „Asymmetrie“ genannt; wir werden es bezeichnen:

In Abb. 5.7.1 zeigt zwei asymmetrische Verteilungen; einer von ihnen (Kurve I) hat eine positive Asymmetrie (); die andere (Kurve II) ist negativ ().

Der vierte zentrale Punkt dient der Charakterisierung der sogenannten „Coolness“, d.h. spitze oder flache Verteilung. Diese Verteilungseigenschaften werden mit der sogenannten Kurtosis beschrieben. Die Kurtosis einer Zufallsvariablen ist die Größe

Die Zahl 3 wird vom Verhältnis abgezogen, da sie in der Natur sehr wichtig und weit verbreitet ist normales Gesetz Verteilung (auf die wir später im Detail eingehen werden). Für eine Normalverteilung ist die Kurtosis also Null; Kurven, die im Vergleich zur Normalkurve stärkere Spitzen aufweisen, weisen eine positive Kurtosis auf; Kurven mit flacheren Spitzen weisen eine negative Kurtosis auf.

In Abb. 5.7.2 zeigt: Normalverteilung (Kurve I), Verteilung mit positiver Kurtosis (Kurve II) und Verteilung mit negativer Kurtosis (Kurve III).

Zusätzlich zu den oben diskutierten Anfangs- und Zentralmomenten werden in der Praxis manchmal die sogenannten absoluten Momente (Anfangs- und Zentralmomente) verwendet, die durch die Formeln bestimmt werden

Offensichtlich fallen absolute Momente gerader Ordnung mit gewöhnlichen Momenten zusammen.

Von den absoluten Momenten wird am häufigsten das erste absolute Zentralmoment verwendet.

, (5.7.21)

wird als arithmetische mittlere Abweichung bezeichnet. Neben Streuung und Standardabweichung wird manchmal auch die arithmetische Mittelabweichung als Merkmal der Streuung verwendet.

Erwartung, Modus, Median, Anfangs- und Zentralmomente und insbesondere Streuung, Standardabweichung, Schiefe und Kurtosis sind die am häufigsten verwendeten numerischen Merkmale von Zufallsvariablen. In vielen Praxisproblemen volle Eigenschaften Eine Zufallsvariable – das Verteilungsgesetz – wird entweder nicht benötigt oder kann nicht ermittelt werden. In diesen Fällen ist man auf eine näherungsweise Beschreibung der Zufallsvariablen mittels Hilfe beschränkt. Numerische Merkmale, die jeweils eine charakteristische Eigenschaft der Verteilung ausdrücken.

Sehr oft werden numerische Merkmale verwendet, um eine Verteilung näherungsweise durch eine andere zu ersetzen, und normalerweise wird versucht, diese Ersetzung so vorzunehmen, dass mehrere wichtige Punkte unverändert bleiben.

Beispiel 1. Es wird ein Experiment durchgeführt, bei dem ein Ereignis auftreten kann oder nicht, dessen Wahrscheinlichkeit gleich ist. Betrachtet wird eine Zufallsvariable – die Häufigkeit des Auftretens eines Ereignisses (charakteristische Zufallsvariable eines Ereignisses). Bestimmen Sie seine Eigenschaften: mathematischer Erwartungswert, Streuung, Standardabweichung.

Lösung. Die Werteverteilungsreihe hat die Form:

Wo ist die Wahrscheinlichkeit, dass das Ereignis nicht eintritt?

Mit der Formel (5.6.1) ermitteln wir den mathematischen Erwartungswert des Wertes:

Die Streuung des Wertes wird durch die Formel (5.7.15) bestimmt:

(Wir schlagen vor, dass der Leser das gleiche Ergebnis erhält, indem er die Streuung anhand des zweiten Anfangsmoments ausdrückt.)

Beispiel 2. Drei unabhängige Schüsse werden auf ein Ziel abgefeuert; Die Wahrscheinlichkeit, jeden Schuss zu treffen, beträgt 0,4. Zufallsvariable – Anzahl der Treffer. Bestimmen Sie die Eigenschaften einer Größe – mathematischer Erwartungswert, Streuung, RSD, Asymmetrie.

Lösung. Die Werteverteilungsreihe hat die Form:

Wir berechnen die numerischen Eigenschaften der Menge.

Finden wir den mathematischen Erwartungswert X 2 :

M(X 2) = 1* 0, 6 + 4* 0, 2 + 25* 0, 19+ 10000* 0, 01 = 106, 15.

Wir sehen das M(X 2) viel mehr M(X). Dies erklärt sich aus der Tatsache, dass nach dem Quadrieren der mögliche Wert der Menge entsteht X 2 entspricht dem Wert X=100 Magnitude X, wurde gleich 10.000, d.h. deutlich erhöht; die Wahrscheinlichkeit dieses Wertes ist gering (0,01).

Somit ist der Übergang von M(X)Zu M(X 2) ermöglichte es, den Einfluss dieses möglichen Werts, der groß und mit geringer Wahrscheinlichkeit ist, auf die mathematische Erwartung besser zu berücksichtigen. Natürlich, wenn der Wert X mehrere große und unwahrscheinliche Werte hatte, dann der Übergang zum Wert X 2, und noch mehr auf die Mengen X 3 , X 4 usw. würden es uns ermöglichen, die Rolle dieser großen, aber unwahrscheinlich möglichen Werte weiter zu „stärken“. Aus diesem Grund erweist es sich als ratsam, die mathematische Erwartung einer ganzzahligen positiven Potenz einer Zufallsvariablen (nicht nur diskret, sondern auch kontinuierlich) zu berücksichtigen.

Anfangszeitpunkt der Ordnung k zufällige Variable X nennt man den mathematischen Erwartungswert einer Größe Xk:

v k = M(X).

Insbesondere,

v 1 = M(X),v 2 = M(X 2).

Aus diesen Punkten ergibt sich die Formel zur Berechnung der Varianz D(X)= M(X 2)- [M(X)] 2 kann wie folgt geschrieben werden:

D(X)=v 2 – . (*)

Zusätzlich zu den Momenten der Zufallsvariablen X Es empfiehlt sich, Abweichungsmomente zu berücksichtigen X-M(X).

Das zentrale Ordnungsmoment k einer Zufallsvariablen X ist der mathematische Erwartungswert der Größe(HM(X))k:

Insbesondere,

Beziehungen, die die Anfangs- und Zentralmomente verbinden, lassen sich leicht ableiten. Wenn wir beispielsweise (*) und (***) vergleichen, erhalten wir

m 2= v 2 – .

Basierend auf der Definition des Zentralmoments und unter Verwendung der Eigenschaften der mathematischen Erwartung ist es nicht schwierig, die Formeln zu erhalten:

m 3= v 3 – 3v 2 v 1 + 2 ,

m 4= v 4 – 4v 3 v 1 + 6v 2 + 3 .

Momente höherer Ordnung werden selten verwendet.

Kommentar. Die hier besprochenen Punkte heißen theoretisch. Im Gegensatz zu theoretischen Momenten werden Momente genannt, die aus Beobachtungsdaten berechnet werden empirisch. Nachfolgend werden Definitionen empirischer Momente gegeben (siehe Kapitel XVII, § 2).

Aufgaben

1. Die Varianzen zweier unabhängiger Zufallsvariablen sind bekannt: D(X) = 4, D(Y)=3. Finden Sie die Varianz der Summe dieser Größen.

Rep. 7.

2. Varianz einer Zufallsvariablen X ist gleich 5. Finden Sie die Varianz der folgenden Größen: a) X-1; b) -2 X; V) ZH + 6.

Rep. a) 5; b) 20; c) 45.

3. Zufälliger Wert X nimmt nur zwei Werte an: +C und -C, jeweils mit einer Wahrscheinlichkeit von 0,5. Finden Sie die Varianz dieser Größe.

Rep. MIT 2 .

4. , das Gesetz seiner Verteilung kennend

X	0, 1
P	0, 4	0, 2	0, 15	0, 25

Rep. 67,6404.

5. Zufälliger Wert X kann zwei mögliche Werte annehmen: X 1 mit Wahrscheinlichkeit 0,3 und X 2 mit einer Wahrscheinlichkeit von 0,7 und X 2 > x 1 . Finden X 1 und X 2, das wissend M(X) = 2, 7i D(X) =0,21.

Rep. X 1 = 2, X 2 = 3.

6. Finden Sie die Varianz einer Zufallsvariablen X-Anzahl des Auftretens von Ereignissen A in zwei unabhängigen Versuchen, wenn M(X) = 0, 8.

Notiz. Schreiben Sie ein Binomialgesetz für die Wahrscheinlichkeitsverteilung der Häufigkeit des Auftretens eines Ereignisses A in zwei unabhängigen Studien.

Rep. 0, 48.

7. Getestet wird ein Gerät bestehend aus vier unabhängig voneinander arbeitenden Geräten. Die Wahrscheinlichkeiten eines Geräteausfalls sind wie folgt: R 1 = 0,3; R 2 = 0,4; P 3 = 0,5; R 4 = 0,6. Ermitteln Sie den mathematischen Erwartungswert und die Varianz der Anzahl ausgefallener Geräte.

Rep. 1,8; 0,94.

8. Finden Sie die Varianz einer Zufallsvariablen X- die Anzahl des Auftretens des Ereignisses in 100 unabhängigen Versuchen, bei denen die Wahrscheinlichkeit des Eintretens des Ereignisses jeweils 0,7 beträgt.

Rep. 21.

9. Varianz einer Zufallsvariablen D(X) = 6,25. Finden Sie die Standardabweichung s( X).

Rep. 2, 5.

10. Die Zufallsvariable wird durch das Verteilungsgesetz festgelegt

X
P	0, 1	0, 5	0, 4

Ermitteln Sie die Standardabweichung dieses Werts.

Rep. 2, 2.

11. Die Varianz jeder der 9 identisch verteilten, voneinander unabhängigen Zufallsvariablen beträgt 36. Ermitteln Sie die Varianz des arithmetischen Mittels dieser Variablen.

Rep. 4.

12. Die Standardabweichung jeder der 16 identisch verteilten, voneinander unabhängigen Zufallsvariablen beträgt 10. Ermitteln Sie die Standardabweichung des arithmetischen Mittels dieser Variablen.

Rep. 2,5.

Kapitel Neun

Gesetz der großen Zahlen

Vorbemerkungen

Welchen der möglichen Werte eine Zufallsvariable als Ergebnis des Tests annehmen wird, lässt sich bekanntlich nicht im Voraus sicher vorhersagen; es hängt von vielen zufälligen Gründen ab, die nicht berücksichtigt werden können. Es scheint, dass es kaum möglich ist, Verhaltensmuster und Summen ausreichend zu ermitteln, da wir über nur sehr bescheidene Informationen über jede Zufallsvariable in diesem Sinne verfügen große Zahl zufällige Variablen. Eigentlich stimmt das nicht. Es stellt sich heraus, dass unter bestimmten relativ allgemeinen Bedingungen das Gesamtverhalten einer ausreichend großen Anzahl von Zufallsvariablen fast seinen Zufallscharakter verliert und natürlich wird.

Für die Praxis ist es sehr wichtig zu wissen, unter welchen Bedingungen das Zusammenwirken vieler Zufallsursachen zu einem nahezu zufallsunabhängigen Ergebnis führt, da es eine Vorhersage des Verlaufs von Phänomenen ermöglicht. Diese Bedingungen sind in den Theoremen angegeben gemeinsamen Namen Gesetz große Zahlen. Dazu gehören die Sätze von Tschebyschew und Bernoulli (es gibt noch andere Sätze, die hier nicht besprochen werden). Der Satz von Tschebyschew ist der am meisten Gewohnheitsrecht Bei großen Zahlen ist der Satz von Bernoulli der einfachste. Um diese Sätze zu beweisen, verwenden wir die Tschebyscheff-Ungleichung.

Tschebyscheffs Ungleichung

Die Tschebyscheff-Ungleichung gilt für diskrete und kontinuierliche Zufallsvariablen. Der Einfachheit halber beschränken wir uns darauf, diese Ungleichung für diskrete Größen zu beweisen.

Betrachten Sie eine diskrete Zufallsvariable X, angegeben durch die Verteilungstabelle:

X	X 1	X 2	…	x n
P	P 1	P 2	…	p n

Stellen wir uns die Aufgabe, die Wahrscheinlichkeit abzuschätzen, dass die Abweichung einer Zufallsvariablen von ihrer mathematischen Erwartung den Absolutwert der positiven Zahl e nicht überschreitet. Wenn e klein genug ist, schätzen wir die Wahrscheinlichkeit dafür ab X wird Werte annehmen, die seiner mathematischen Erwartung ziemlich nahe kommen. P. L. Chebyshev hat eine Ungleichung bewiesen, die es uns ermöglicht, die Schätzung anzugeben, an der wir interessiert sind.

Tschebyscheffs Ungleichung. Die Wahrscheinlichkeit, dass die Abweichung einer Zufallsvariablen X von ihrer mathematischen Erwartung im absoluten Wert kleiner als eine positive Zahl e ist, beträgt nicht weniger als 1-D(X)/e 2 :

R(|X -M(X)|< e ) 1-D(X)/e 2 .

Nachweisen. Da Ereignisse in der Umsetzung von Ungleichheiten bestehen |X-M(X)| Und |X-M(X)| e, entgegengesetzt sind, dann ist die Summe ihrer Wahrscheinlichkeiten gleich eins, d.h.

R(|X -M(X)|< e )+ R(|X -M(X)| e)= 1.

Daher die Wahrscheinlichkeit, die uns interessiert

R(|X -M(X)|< e )= 1- R(|X -M(X)| e). (*)

Das Problem besteht also darin, die Wahrscheinlichkeit zu berechnen R(| HM(X)| e).

Schreiben wir den Ausdruck für die Varianz der Zufallsvariablen X:

D(X)= [X 1 -M(X)] 2 P 1 + [X 2 -M(X)] 2 P 2 +…+ [x n -M(X)]2pn.

Offensichtlich sind alle Terme dieser Summe nicht negativ.

Lassen Sie uns die Begriffe verwerfen, für die | x i-M(X)|<e(für die restlichen Begriffe | x j-M(X)| e), Dadurch kann sich der Betrag nur verringern. Lassen Sie uns der Sicherheit halber davon ausgehen, dass die k die ersten Terme (ohne Beschränkung der Allgemeinheit können wir davon ausgehen, dass in der Verteilungstabelle die möglichen Werte in genau dieser Reihenfolge nummeriert sind). Auf diese Weise,

D(X) [x k + 1 -M(X)] 2 p k + 1 + [x k + 2 -M(X)] 2 p k + z + ... +[x n -M(X)] 2 pn.

Beachten Sie, dass beide Seiten der Ungleichung | x j - M(X)| e (J = k+1, k+ 2, ..., P) sind positiv, daher erhalten wir durch Quadrieren die äquivalente Ungleichung | x j - M(X)| 2 e 2 Lassen Sie uns diese Bemerkung verwenden und jeden der Faktoren in der verbleibenden Summe | ersetzen x j - M(X)| 2 an der Zahl e 2(in diesem Fall kann die Ungleichung nur zunehmen), erhalten wir

D(X) e 2 (r k+ 1 + p k + 2 + … + ð n). (**)

Nach dem Additionssatz ist die Summe der Wahrscheinlichkeiten r k+ 1 + p k + 2 + … + ð n Es besteht die Möglichkeit, dass X wird einen, egal welchen, Wert annehmen x k + 1 , x k+ 2 ,....x p, und für jeden von ihnen erfüllt die Abweichung die Ungleichung | x j - M(X)| e Daraus ergibt sich der Betrag r k+ 1 + p k + 2 + … + ð n drückt die Wahrscheinlichkeit aus

P(|X - M(X)| e).

Diese Überlegung ermöglicht es uns, die Ungleichung (**) wie folgt umzuschreiben:

D(X) e 2 P(|X - M(X)| e),

P(|X - M(X)| e)D(X) /e 2 (***)

Wenn wir (***) durch (*) ersetzen, erhalten wir schließlich

P(|X - M(X)| <e) 1-D(X) /e 2 ,

Q.E.D.

Kommentar. Tschebyscheffs Ungleichung hat nur begrenzte praktische Bedeutung, da sie oft eine grobe und manchmal triviale (uninteressante) Schätzung liefert. Zum Beispiel, wenn D(X)>E 2 und daher D(X)/e 2 > 1, dann 1 -D(X)/e 2 < 0; In diesem Fall weist die Tschebyscheff-Ungleichung also lediglich darauf hin, dass die Wahrscheinlichkeit einer Abweichung nicht negativ ist, und dies ist bereits offensichtlich, da jede Wahrscheinlichkeit durch eine nicht negative Zahl ausgedrückt wird.

Die theoretische Bedeutung der Tschebyscheff-Ungleichung ist sehr groß. Im Folgenden werden wir diese Ungleichung verwenden, um den Satz von Tschebyscheff abzuleiten.

Satz von Tschebyschew

Satz von Tschebyschew. Wenn X 1 , X 2 ,…, X n, ...-paarweise unabhängige Zufallsvariablen und ihre Varianzen sind gleichmäßig beschränkt(eine konstante Zahl C nicht überschreiten), dann ist die Wahrscheinlichkeit der Ungleichheit egal, wie klein die positive Zahl e ist

Mit anderen Worten, unter den Bedingungen des Satzes

So besagt der Satz von Tschebyschew, dass, wenn eine ausreichend große Anzahl unabhängiger Zufallsvariablen mit begrenzten Varianzen berücksichtigt wird, das Ereignis als nahezu zuverlässig angesehen werden kann, das darin besteht, dass die Abweichung des arithmetischen Mittels von Zufallsvariablen vom arithmetischen Mittel ihrer Mathematische Erwartungen werden im Absolutwert beliebig groß und klein sein

Nachweisen. Lassen Sie uns eine neue Zufallsvariable in Betracht ziehen – das arithmetische Mittel von Zufallsvariablen

=(X 1 +X 2 +…+X n)/N.

Finden wir den mathematischen Erwartungswert . Unter Verwendung der Eigenschaften des mathematischen Erwartungswerts (der konstante Faktor kann aus dem Vorzeichen des mathematischen Erwartungswerts entnommen werden, der mathematische Erwartungswert der Summe ist gleich der Summe der mathematischen Erwartungswerte der Terme) erhalten wir

M = . (*)

Wenn wir Tschebyscheffs Ungleichung auf die Menge anwenden, erhalten wir

Wenn wir die rechte Seite (***) in die Ungleichung (**) einsetzen (weshalb letztere nur verstärkt werden kann), haben wir

Von hier aus erhalten wir, wenn wir zum Grenzwert bei gehen

Unter Berücksichtigung der Tatsache, dass die Wahrscheinlichkeit eins nicht überschreiten darf, können wir schließlich schreiben

Der Satz ist bewiesen.

Oben haben wir bei der Formulierung des Chebyshev-Theorems angenommen, dass Zufallsvariablen unterschiedliche mathematische Erwartungen haben. In der Praxis kommt es häufig vor, dass Zufallsvariablen denselben mathematischen Erwartungswert haben. Wenn wir wiederum davon ausgehen, dass die Streuungen dieser Größen begrenzt sind, ist der Satz von Tschebyscheff natürlich auf sie anwendbar.

Bezeichnen wir den mathematischen Erwartungswert jeder der Zufallsvariablen mit A; im vorliegenden Fall ist, wie leicht zu erkennen ist, auch das arithmetische Mittel der mathematischen Erwartungen gleich A. Wir können den Satz von Tschebyschew für den jeweiligen betrachteten Fall formulieren.

Wenn X 1 , X 2 , ..., PS...-paarweise unabhängige Zufallsvariablen, die den gleichen mathematischen Erwartungswert a haben, und wenn die Varianzen dieser Variablen gleichmäßig begrenzt sind, egal wie klein die Zahl e ist>Oh, Wahrscheinlichkeit der Ungleichheit

wird so nah wie gewünscht an Eins liegen, wenn die Anzahl der Zufallsvariablen groß genug ist.

Mit anderen Worten, unter den Bedingungen des Satzes wird Gleichheit herrschen

Die Essenz des Satzes von Tschebyschew

Der Kern des bewährten Theorems lautet wie folgt: Obwohl einzelne unabhängige Zufallsvariablen Werte annehmen können, die weit von ihren mathematischen Erwartungen entfernt sind, nimmt das arithmetische Mittel einer ausreichend großen Anzahl von Zufallsvariablen mit hoher Wahrscheinlichkeit Werte nahe einem bestimmten an konstante Zahl, nämlich auf die Zahl ( M(X 1)+ M(X 2)+...+M(X p))/P(oder auf die Nummer A in einem besonderen Fall). Mit anderen Worten: Einzelne Zufallsvariablen können eine erhebliche Streuung aufweisen und ihr arithmetisches Mittel ist streuend klein.

Daher kann man nicht sicher vorhersagen, welchen möglichen Wert jede der Zufallsvariablen annehmen wird, aber man kann vorhersagen, welchen Wert ihr arithmetisches Mittel annehmen wird.

Also, arithmetisches Mittel einer ausreichend großen Anzahl unabhängiger Zufallsvariablen(deren Varianzen gleichmäßig beschränkt sind) verliert den Charakter einer Zufallsvariablen. Dies erklärt sich dadurch, dass die Abweichungen jedes Wertes von seinen mathematischen Erwartungen sowohl positiv als auch negativ sein können und sich im arithmetischen Mittel gegenseitig aufheben.

Der Satz von Chebyshev gilt nicht nur für diskrete, sondern auch für kontinuierliche Zufallsvariablen; das ist sie zufällig ein leuchtendes Beispiel, was die Gültigkeit der Lehre des dialektischen Materialismus über den Zusammenhang zwischen Zufall und Notwendigkeit bestätigt.