Anwendungsbeispiele für Raubtier-Beutemodelle. Schwingungen des Räuber-Beute-Systems (Lotka-Voltaire-Modell). Klassisches Volterra-Modell
Annahmen:
1. Das Medium ist homogen.
2. Die Häufigkeit einer bestimmten Art wird durch eine Variable beschrieben, d. h. Wir vernachlässigen Alter, Geschlecht und genetische Unterschiede.
3. Wir vernachlässigen zufällige Schwankungen.
4. Die Interaktion erfolgt sofort.
In der biologischen Literatur gibt es eine Vielzahl von Studien, in denen solche Systeme entweder in der Natur beobachtet oder an „Modell“-Populationen unter Laborbedingungen simuliert wurden.
Ihre Ergebnisse sind jedoch oft widersprechen gegenseitig:
− In einigen Experimenten wurden auf den ersten Blick unverständliche Phänomene periodischer Veränderungen der Bevölkerungszahlen in einer homogenen Umgebung beobachtet;
- In anderen Beobachtungen kollabierten Systeme recht schnell: Entweder das Raubtier stirbt, aber die Beute bleibt, oder die Beute stirbt, gefolgt vom Raubtier.
Vito Voltaires in den 1920er Jahren entwickeltes Modell der Raubtier-Beute-Gemeinschaft erklärt viele dieser Merkmale.
Dies ist der erste Erfolg der mathematischen Ökologie.
Bei der Betrachtung dieses Systems werden wir Fragen der Nachhaltigkeit berücksichtigen: Bedingungen für Nachhaltigkeit und Mechanismen der Nachhaltigkeit.
Klassisches Volterra-Modell
Anzahl der Raubtiere.
Zusätzliche Annahmen.
1. Der einzige limitierende Faktor, der die Fortpflanzung von Beutetieren einschränkt, ist der Druck, der von Raubtieren auf sie ausgeübt wird. Die begrenzten Ressourcen der Umwelt für das Opfer werden nicht berücksichtigt (wie im Malthus-Modell).
2. Die Fortpflanzung von Raubtieren wird durch die Menge an Nahrung, die sie erhalten (die Anzahl der Opfer), begrenzt.
− Koeffizient des natürlichen Wachstums des Opfers;
− Koeffizient natürliche Sterblichkeit Raubtier;
− Anzahl (Biomasse) der Beute, die ein Raubtier pro Zeiteinheit verzehrt (trophische Funktion);
− Teil der aus Biomasse gewonnenen Energie, die vom Raubtier zur Fortpflanzung aufgewendet wird. Der Rest der Energie wird für die Aufrechterhaltung des Grundstoffwechsels und der Jagdaktivität aufgewendet.
Gleichungen des Raubtier-Beutesystems
Die Funktion wird in experimentellen Arbeiten ermittelt. Es wurde nun festgestellt, dass diese Funktionen zu einem der folgenden drei Typen gehören.
Diese Art ist charakteristisch für Wirbellose und einige Raubfischarten.
Charakteristisch für Raubtiere – Filterfresser (Mollusken) – ist eine trophische Funktion mit einer ausgeprägten Sättigungsschwelle.
Dieser Typ ist charakteristisch für Wirbeltiere – lernfähige Organismen.
Bei geringen Beutezahlen werden fast alle Beutetiere zur Beute eines Raubtiers, das immer hungrig ist und nicht satt wird. Die trophische Funktion kann als linear betrachtet werden:
Klassisches Volterra-Modell:
Anfangsbedingungen
System (2) ist autonom, weil hat nicht auf der rechten Seite. Die Zustandsänderung des Systems wird auf der Phasenebene dargestellt und ist eine Lösung der Gleichung
Finden wir die Ruhepunkte des Systems (2).
Der nichttriviale Ruhepunkt des Systems (4) hat die Form
Lassen Sie uns die Art des Ruhepunkts (5) bestimmen.
Machen wir einen Ersatz
Öffnen wir die Klammern und holen uns das System
Wenn wir die nichtlinearen Terme verwerfen, erhalten wir das System
Die charakteristische Gleichung hat die Form
Die Wurzeln sind rein imaginäre Zahlen. Der Ruhepunkt ist die Mitte. In den Anfangsvariablen haben die Phasentrajektorien die Form
Die Pfeile geben die Richtung der Zustandsänderung des Systems im Zeitverlauf an.
Entsprechend dieser Bewegung entlang der Flugbahn unterliegen die Populationszahlen von Räuber und Beute ungedämpften periodischen Schwankungen, und die Schwankungen in der Zahl des Raubtiers hinken den Schwankungen in der Zahl der Beute phasengleich hinterher (um ein Viertel der Periode). .
Das Phasenporträt der Lösung hat die Form einer Spirale:
Im „Raubtier-Beute“-System gibt es gedämpfte Schwingungen. Die Beute- und Raubtierzahlen tendieren zu ihren Gleichgewichtswerten (8).
Diagramme der Artenhäufigkeit.
Modelle der Interaktion zweier Typen
Volterras Hypothesen. Analogien zur chemischen Kinetik. Volterra-Interaktionsmodelle. Klassifizierung der Interaktionsarten Wettbewerb. Raubtier-Beute. Verallgemeinerte Modelle der Arteninteraktionen . Kolmogorov-Modell. MacArthurs Modell der Interaktion zwischen zwei Insektenarten. Parametrisch und Phasenporträts des Bazykin-Systems.
Als Begründer der modernen mathematischen Populationstheorie gilt zu Recht der italienische Mathematiker Vito Volterra, der die mathematische Theorie biologischer Gemeinschaften entwickelte, deren Apparat Differential- und Integro-Differentialgleichungen sind.(Vito Volterra. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. Paris, 1931). In den folgenden Jahrzehnten entwickelte sich die Bevölkerungsdynamik hauptsächlich im Einklang mit den in diesem Buch zum Ausdruck gebrachten Ideen. Die russische Übersetzung von Volterras Buch wurde 1976 unter dem Titel veröffentlicht: „ Mathematische Theorie Kampf ums Dasein“ mit einem Nachwort von Yu.M. Svirezhev, der die Entwicklungsgeschichte der mathematischen Ökologie im Zeitraum 1931–1976 untersucht.
Volterras Buch ist so geschrieben, wie Bücher über Mathematik geschrieben werden. Es formuliert zunächst einige Annahmen über die mathematischen Objekte, die untersucht werden sollen, und führt dann eine mathematische Untersuchung der Eigenschaften dieser Objekte durch.
Die von Volterra untersuchten Systeme bestehen aus zwei oder mehr Typen. Teilweise wird auch die Versorgung mit eingesetzten Lebensmitteln berücksichtigt. Die Gleichungen, die die Interaktion dieser Typen beschreiben, basieren auf den folgenden Konzepten.
Volterras Hypothesen
1. Lebensmittel sind entweder in unbegrenzter Menge verfügbar oder ihre Versorgung ist über die Zeit streng reguliert.
2. Individuen jeder Art sterben so ab, dass pro Zeiteinheit ein konstanter Anteil der vorhandenen Individuen stirbt.
3. Raubtierarten fressen Opfer, und pro Zeiteinheit ist die Anzahl der gefressenen Opfer immer proportional zur Wahrscheinlichkeit, Individuen dieser beiden Arten zu treffen, d.h. das Produkt aus der Anzahl der Raubtiere und der Anzahl der Beutetiere.
4. Wenn Nahrung in begrenzten Mengen vorhanden ist und mehrere Arten diese verzehren können, dann ist der Anteil der von einer Art pro Zeiteinheit verzehrten Nahrung proportional zur Anzahl der Individuen dieser Art, genommen mit einem bestimmten Koeffizienten abhängig von der Arten (Modelle des interspezifischen Wettbewerbs).
5. Wenn sich eine Art von Nahrungsmitteln ernährt, die in unbegrenzten Mengen verfügbar sind, ist die Zunahme der Anzahl der Arten pro Zeiteinheit proportional zur Anzahl der Arten.
6. Wenn sich eine Art von Nahrung ernährt, die in begrenzten Mengen verfügbar ist, wird ihre Fortpflanzung durch die Geschwindigkeit des Nahrungsverbrauchs reguliert, d. h. pro Zeiteinheit ist der Anstieg proportional zur aufgenommenen Nahrungsmenge.
Analogien zur chemischen Kinetik
Diese Hypothesen weisen enge Parallelen zur chemischen Kinetik auf. In den Gleichungen der Populationsdynamik wird wie in den Gleichungen der chemischen Kinetik das „Kollisionsprinzip“ verwendet, bei dem die Reaktionsgeschwindigkeit proportional zum Produkt der Konzentrationen der reagierenden Komponenten ist.
Tatsächlich, nach Volterras Hypothesen, die Geschwindigkeit Verfahren Das Aussterben jeder Art ist proportional zur Anzahl der Arten. In der chemischen Kinetik entspricht dies einer monomolekularen Reaktion der Zersetzung einer Substanz und in mathematisches Modell– negative lineare Terme auf der rechten Seite der Gleichungen.
Nach den Konzepten der chemischen Kinetik ist die Geschwindigkeit der bimolekularen Wechselwirkungsreaktion zwischen zwei Stoffen proportional zur Kollisionswahrscheinlichkeit dieser Stoffe, d.h. das Produkt ihrer Konzentration. In gleicher Weise ist gemäß den Hypothesen von Volterra die Reproduktionsrate von Raubtieren (Beutetod) proportional zur Wahrscheinlichkeit von Begegnungen zwischen Raubtier und Beutetier, d. h. das Produkt ihrer Zahlen. In beiden Fällen erscheinen bilineare Terme im Modellsystem auf der rechten Seite der entsprechenden Gleichungen.
Schließlich entsprechen die linearen positiven Terme auf der rechten Seite der Volterra-Gleichungen, die dem Bevölkerungswachstum unter unbegrenzten Bedingungen entsprechen, den autokatalytischen Termen chemische Reaktionen. Diese Ähnlichkeit der Gleichungen in chemischen und Umweltmodellen ermöglicht es uns, für die mathematische Modellierung der Populationskinetik dieselben Forschungsmethoden anzuwenden wie für Systeme chemischer Reaktionen.
Klassifizierung von Interaktionsarten
In Übereinstimmung mit Volterras Hypothesen ist das Zusammenspiel zweier Arten, deren Anzahl X 1 und X 2 kann durch die Gleichungen beschrieben werden:
(9.1)
Hier sind die Parameter A ich - Konstanten der arteigenen Wachstumsrate, C ich- Konstanten der Selbstbeschränkung der Zahlen (intraspezifische Konkurrenz), b ij- Arteninteraktionskonstanten, (ich, j= 1,2). Die Vorzeichen dieser Koeffizienten bestimmen die Art der Wechselwirkung.
In der biologischen Literatur werden Wechselwirkungen üblicherweise nach den beteiligten Mechanismen klassifiziert. Die Vielfalt hier ist enorm: verschiedene trophische Wechselwirkungen, chemische Wechselwirkungen, die zwischen Bakterien und Bakterien bestehen planktonische Algen, Wechselwirkungen von Pilzen mit anderen Organismen, Sukzession pflanzlicher Organismen, insbesondere verbunden mit der Konkurrenz um Sonnenlicht und mit der Entwicklung der Böden usw. Diese Klassifizierung erscheint umfangreich.
E . Odum schlug unter Berücksichtigung der von V. Volterra vorgeschlagenen Modelle eine Klassifizierung nicht nach Mechanismen, sondern nach Ergebnissen vor. Nach dieser Klassifizierung sind Beziehungen als positiv, negativ oder neutral zu bewerten, je nachdem, ob die Häufigkeit einer Art in Anwesenheit einer anderen Art zunimmt, abnimmt oder unverändert bleibt. Anschließend können die wichtigsten Interaktionsarten tabellarisch dargestellt werden.
ARTEN DER INTERAKTION VON ARTEN
|
SYMBIOSE |
B 12 ,B 21 >0 |
||
|
KOMMENSALISMUS |
B 12 ,>0, B 21 =0 |
||
|
Raubtier-Opfer |
B 12 ,>0, B 21 <0 |
||
|
AMENSALISMUS |
B 12 ,=0, B 21 <0 |
||
|
WETTBEWERB |
B 12 , B 21 <0 |
||
|
NEUTRALISMUS |
B 12 , B 21 =0 |
Die letzte Spalte zeigt die Vorzeichen der Wechselwirkungskoeffizienten aus System (9.1)
Schauen wir uns die wichtigsten Arten von Interaktionen an
WETTBEWERBSGLEICHUNGEN:
Wie wir in Vorlesung 6 gesehen haben, lauten die Wettbewerbsgleichungen:
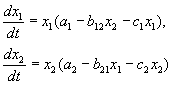 (9.2)
(9.2)
Stationäre Systemlösungen:
(1).
![]()
Der Koordinatenursprung für alle Systemparameter ist ein instabiler Knoten.
(2).
![]() (9.3)
(9.3)
C Der stationäre Zustand (9.3) ist ein Sattel A 1 >b 12 /Mit 2 und
stabiler Knoten bei A 1 12 /s 2 . Diese Bedingung bedeutet, dass eine Art ausstirbt, wenn ihre eigene Wachstumsrate einen bestimmten kritischen Wert unterschreitet.
(3).
![]() (9.4)
(9.4)
C stationäre Lösung (9.4)¾ Sattel bei A 2 >b 21 /C 1 und ein stabiler Knoten bei A 2< B 21 /C 1
(4).
![]() (9.5)
(9.5)
Der stationäre Zustand (9.5) charakterisiert die Koexistenz zweier konkurrierender Arten und stellt einen stabilen Knoten dar, wenn die Beziehung erfüllt ist:
![]()
Dies impliziert die Ungleichung:
B 12
B 21
Damit können wir die Bedingung für das Zusammenleben von Arten formulieren:
Das Produkt der Koeffizienten der Interaktion zwischen Populationen ist kleiner als das Produkt der Koeffizienten innerhalb der Interaktion zwischen Populationen.
Lassen Sie in der Tat die natürlichen Wachstumsraten der beiden Arten in Betracht ziehenA 1 , A 2 sind gleich. Dann ist die notwendige Voraussetzung für Stabilität gegeben
C 2 > B 12 ,C 1 >b 21 .
Diese Ungleichheiten zeigen, dass eine Vergrößerung eines Konkurrenten sein eigenes Wachstum stärker unterdrückt als das Wachstum eines anderen Konkurrenten. Wenn die Anzahl beider Arten teilweise oder vollständig durch unterschiedliche Ressourcen begrenzt ist, gelten die oben genannten Ungleichungen. Wenn beide Arten genau die gleichen Bedürfnisse haben, ist eine von ihnen lebensfähiger und verdrängt ihren Konkurrenten.
Das Verhalten der Phasentrajektorien des Systems gibt eine klare Vorstellung von den möglichen Ergebnissen des Wettbewerbs. Setzen wir die rechten Seiten der Gleichungen des Systems (9.2) mit Null gleich:
X 1 (A 1 –c 1 X 1 – B 12 X 2) = 0 (dx 1 /dt = 0),
X 2 (A 2 –B 21 X 1 – C 2 X 2) = 0 (dx 2 /dt = 0),
In diesem Fall erhalten wir Gleichungen für die Hauptisoklinen des Systems
X 2 = – b 21 X 1 / C 2 +A 2 /c 2, X 2 = 0
– Gleichungen der Isoklinen vertikaler Tangenten.
X 2 = – c 1 X 1 / b 12 + A 1 /B 12 , X 1 = 0
– Gleichungen der Isoklinen vertikaler Tangenten. Die paarweisen Schnittpunkte der Isoklinen vertikaler und horizontaler Tangentensysteme stellen stationäre Lösungen des Gleichungssystems (9.2.) und deren Koordinaten dar ![]() sind stationäre Zahlen konkurrierender Arten.
sind stationäre Zahlen konkurrierender Arten.
Die mögliche Lage der Hauptisoklinen im System (9.2) ist in Abb. 9.1 dargestellt. Reis. 9.1Aentspricht dem Überleben der ArtX 1, Abb. 9.1 B– Überleben der ArtX 2, Abb. 9.1 V– Koexistenz von Arten, wenn Bedingung (9.6) erfüllt ist. Abbildung 9.1Gdemonstriert das Auslösesystem. Dabei hängt der Ausgang des Wettbewerbs von den Ausgangsbedingungen ab. Der von Null verschiedene stationäre Zustand (9.5) ist für beide Typen instabil. Dies ist der Sattel, durch den die Separatrix verläuft und der die Überlebensbereiche der einzelnen Arten trennt.

Reis. 9.1.Lage der Hauptisoklinen im Phasenporträt des Volterra-Konkurrenzsystems zweier Typen (9.2) mit unterschiedlichen Parameterverhältnissen. Erläuterungen im Text.
Zur Untersuchung der Artenkonkurrenz wurden Experimente an verschiedensten Organismen durchgeführt. Typischerweise werden zwei eng verwandte Arten ausgewählt und gemeinsam und getrennt unter streng kontrollierten Bedingungen gezüchtet. In bestimmten Abständen wird eine vollständige oder selektive Volkszählung durchgeführt. Daten aus mehreren Wiederholungsexperimenten werden aufgezeichnet und analysiert. Es wurden Studien an Protozoen (insbesondere Ciliaten), vielen Käferarten der Gattung Tribolium, Drosophila und Süßwasserkrebstieren (Daphnien) durchgeführt. Viele Experimente wurden an mikrobiellen Populationen durchgeführt (siehe Vorlesung 11). Experimente wurden auch in der Natur durchgeführt, unter anderem an Planarien (Reynolds), zwei Ameisenarten (Pontin) usw. In Abb. 9.2. stellt die Wachstumskurven von Kieselalgen dar, die dieselbe Ressource nutzen (und dieselbe ökologische Nische besetzen). Beim Anbau in Monokultur Asterionella Formosa erreicht eine konstante Dichte und hält die Konzentration des Rohstoffes (Silikat) auf einem konstant niedrigen Niveau. B. Beim Anbau in Monokultur Synedrauina verhält sich ähnlich und hält die Silikatkonzentration auf einem noch niedrigeren Niveau. B. Während der Co-Kultivierung (im Duplikat) Synedrauina verdrängt Asterionella formosa. Anscheinend Synedra

Reis. 9.2.Konkurrenz bei Kieselalgen. A - wenn es in Monokultur angebaut wird Asterionella Formosa erreicht eine konstante Dichte und hält die Konzentration des Rohstoffes (Silikat) auf einem konstant niedrigen Niveau. B - wenn es in Monokultur angebaut wird Synedrauina verhält sich ähnlich und hält die Silikatkonzentration auf einem noch niedrigeren Niveau. V - mit Co-Anbau (im Doppel) Synedruina verdrängt Asterionella formosa. Anscheinend Synedra gewinnt den Wettbewerb aufgrund seiner Fähigkeit, das Substrat besser auszunutzen (siehe auch Vorlesung 11).
Weithin bekannt sind die Experimente von G. Gause zur Untersuchung des Wettbewerbs, die das Überleben einer der konkurrierenden Arten belegen und es ihm ermöglichen, das „Gesetz des Wettbewerbsausschlusses“ zu formulieren. Das Gesetz besagt, dass in einer ökologischen Nische nur eine Art existieren darf. In Abb. 9.3. Die Ergebnisse von Gauses Experimenten werden für zwei Parametium-Arten präsentiert, die dieselbe ökologische Nische besetzen (Abb. 9.3 a, b) und für Arten, die unterschiedliche ökologische Nischen besetzen (Abb. 9.3 c).

Reis. 9.3. A- Populationswachstumskurven zweier Arten Parametium in Einzelkulturen. Schwarze Kreise – P Aurelia, weiße Kreise – P. Caudatum
B- Wachstumskurven von P Aurelia und P . Caudatum in einer gemischten Kultur.
Von Gause, 1934
Das Konkurrenzmodell (9.2) hat Nachteile, insbesondere folgt daraus, dass die Koexistenz zweier Arten nur dann möglich ist, wenn ihre Anzahl durch unterschiedliche Faktoren begrenzt wird, das Modell aber nicht angibt, wie groß die Unterschiede sein müssen, um eine langfristige Koexistenz zu gewährleisten . Gleichzeitig ist bekannt, dass für ein langfristiges Zusammenleben in einem sich verändernden Umfeld ein Unterschied in einer bestimmten Größenordnung notwendig ist. Durch die Einführung stochastischer Elemente in das Modell (z. B. die Einführung einer Ressourcennutzungsfunktion) können wir diese Probleme quantitativ untersuchen.
PREDATOR+VICTIM-System
 (9.7)
(9.7)
Hier im Gegensatz zu (9.2) die Vorzeichen B 12 Und B 21 sind unterschiedlich. Wie im Fall des Wettbewerbs der Ursprung
![]() (9.8)
(9.8)
ist ein spezieller Punkt vom Typ instabiler Knoten. Drei weitere mögliche stationäre Zustände:
![]() ,(9.9)
,(9.9)
![]() (9.10)
(9.10)
![]() (9.11)
(9.11)
Somit ist das Überleben nur der Beute (9.10), nur des Raubtiers (9.9) (sofern es über andere Nahrungsquellen verfügt) und das Zusammenleben beider Arten (9.11) möglich. Die letzte Option haben wir bereits in Vorlesung 5 besprochen. Mögliche Arten von Phasenporträts für ein Räuber-Beute-System sind in Abb. dargestellt. 9.4.
Isoklinen horizontaler Tangenten sind Geraden
X 2 = – B 21 X 1 /C 2 + A 1/c 2, X 2 = 0,
und Isoklinen vertikaler Tangenten- gerade
X 2 = – C 1 X 1 /B 12 + A 2 /B 12 , X 1 = 0.
Stationäre Punkte liegen am Schnittpunkt vertikaler und horizontaler Tangenten-Isoklinen.

Aus Abb. 9.4 Folgendes ist sichtbar. Raubtier-Beute-System (9.7) kann eine stabile Gleichgewichtslage haben, in derÖ Die Rumpopulation der Opfer ist vollständig ausgestorben ( ) und nur Raubtiere blieben übrig (Punkt 2 in Abb. 9.4 A). Offensichtlich kann eine solche Situation nur dann realisiert werden, wenn neben der Art der betrachteten Opfer auch X 1 Raubtier X 2 – verfügt über zusätzliche Stromquellen. Diese Tatsache spiegelt sich im Modell durch den positiven Term auf der rechten Seite der Gleichung für x2 wider. Besondere Punkte(1) und (3) (Abb. 9.4 A) sind instabil. Zweite Möglichkeit – ein stabiler stationärer Zustand, in dem die Raubtierpopulation vollständig ausgestorben ist und nur noch Beute übrig bleibt – stabiler Punkt(3) (Abb. 9.4 6 ). Hier singulärer Punkt (1) – auch ein instabiler Knoten.
Zum Schluss noch die dritte Möglichkeit – nachhaltige Koexistenz von Raubtier- und Beutepopulationen (Abb. 9.4 V), deren stationäre Zahlen durch die Formeln ausgedrückt werden (9.11).
Wie im Fall einer Population (siehe Vorlesung 3) für das Modell (9.7) Es ist möglich, ein stochastisches Modell zu entwickeln, es kann jedoch nicht explizit gelöst werden. Daher beschränken wir uns auf allgemeine Betrachtungen. Nehmen wir zum Beispiel an, dass der Gleichgewichtspunkt in einem bestimmten Abstand von jeder der Achsen liegt. Dann für Phasentrajektorien, auf denen die Werte liegenX 1 , X 2 groß genug bleiben, wird ein deterministisches Modell durchaus zufriedenstellend sein. Wenn jedoch an einem bestimmten Punkt der Phasentrajektorie eine Variable nicht sehr groß ist, können zufällige Schwankungen erheblich werden. Sie führen dazu, dass sich der darstellende Punkt in eine der Achsen verschiebt, was das Aussterben der entsprechenden Art bedeutet.
Somit erweist sich das stochastische Modell als instabil, da die stochastische „Drift“ früher oder später zum Aussterben einer der Arten führt. In einem solchen Modell stirbt das Raubtier schließlich aus, entweder durch Zufall oder weil seine Beutepopulation zuerst vernichtet wird. Das stochastische Modell des Räuber-Beute-Systems erklärt Gause‘s Experimente gut (Gause, 1934), in denen Ciliaten Paramettum candatum diente als Beute für einen anderen Wimpertier Didinium nasatum – Raubtier. Erwartet nach deterministischen Gleichungen (9.7) Die Gleichgewichtszahlen in diesen Experimenten betrugen etwa nur fünf Individuen jeder Art, daher ist es nicht verwunderlich, dass bei jedem wiederholten Experiment entweder die Raubtiere oder die Beute (und danach die Raubtiere) ziemlich schnell ausstarben. Die Ergebnisse der Experimente werden vorgestellt in Abb. 9.5.

Reis. 9.5. Höhe Parametium caudatum und räuberische Ciliaten Dadinium nasutum. Aus : Gause G.F. Der Kampf ums Dasein. Baltimore, 1934
Die Analyse von Volterra-Modellen der Arteninteraktion zeigt also, dass es trotz der großen Verhaltensvielfalt solcher Systeme im Modell konkurrierender Arten überhaupt keine ungedämpften Zahlenschwankungen geben kann. Allerdings werden solche Schwingungen in der Natur und im Experiment beobachtet. Die Notwendigkeit ihrer theoretischen Erklärung war einer der Gründe, Modellbeschreibungen in einer allgemeineren Form zu formulieren.
Verallgemeinerte Modelle der Interaktion zweier Typen
Zur Beschreibung der Interaktion von Arten wurde eine große Anzahl von Modellen vorgeschlagen, deren rechte Seite der Gleichungen Funktionen der Anzahl der interagierenden Populationen waren. Das Problem der Entwicklung allgemeiner Kriterien zur Feststellung, welche Art von Funktionen das Verhalten der temporären Populationsgröße, einschließlich stabiler Schwankungen, beschreiben können, wurde gelöst. Die bekanntesten dieser Modelle gehören Kolmogorov (1935, überarbeiteter Artikel – 1972) und Rosenzweig (1963).
 (9.12)
(9.12)
Das Modell beinhaltet die folgenden Annahmen:
1) Raubtiere interagieren nicht miteinander, d.h. Reproduktionsrate der Raubtiere k 2 und Anzahl der Opfer L pro Zeiteinheit von einem Raubtier ausgerottet wird, hängt nicht davon ab j.
2) Die Zunahme der Beutezahl in Anwesenheit von Raubtieren entspricht der Zunahme in Abwesenheit von Raubtieren abzüglich der Zahl der von Raubtieren ausgerotteten Beutetiere. Funktionen k 1 (X), k 2 (X), L(X), - sind stetig und auf der positiven Halbachse definiert X, j³ 0.
3) dk 1 /dx< 0. Dies bedeutet, dass die Reproduktionsrate von Beutetieren in Abwesenheit eines Raubtiers mit zunehmender Anzahl von Beutetieren monoton abnimmt, was die begrenzte Verfügbarkeit von Nahrungsmitteln und anderen Ressourcen widerspiegelt.
4) dk 2 /dx> 0, k 2 (0) < 0 < k 2 (¥ ). Mit zunehmender Beutezahl nimmt der Reproduktionskoeffizient von Raubtieren mit zunehmender Beutezahl monoton ab negative Werte, (wenn es nichts zu essen gibt) bis positiv.
5) Die Anzahl der Beute, die von einem Raubtier pro Zeiteinheit zerstört wird L(X)> 0 bei N> 0; L(0)=0.
Mögliche Arten von Phasenporträts des Systems (9.12) sind in Abb. dargestellt. 9.6:

Reis. 9.6.Phasenporträts des Kolmogorov-Systems (9.12), das die Wechselwirkung zweier Typen bei unterschiedlichen Parameterverhältnissen beschreibt. Erläuterungen im Text.
Stationäre Lösungen (es gibt zwei oder drei) haben die folgenden Koordinaten:
(1). ` x=0;` y=0.
Der Koordinatenursprung für beliebige Parameterwerte ist ein Sattel (Abb. 9.6 a-d).
(2). ` x=A,` y=0.(9.13)
Aermittelt aus der Gleichung:
k 1 (A)=0.
Stationär Lösung (9.13) ist ein Sattel wenn B< A (Abb. 9.6 A, B, G), B aus der Gleichung ermittelt
k 2 (B)=0
Punkt (9.13) wird in den positiven Quadranten gelegt, wenn B>A . Dies ist ein stabiler Knoten .
Der letzte Fall, der dem Tod des Raubtiers und dem Überleben der Beute entspricht, ist in Abb. dargestellt. 9.6 V.
(3). ` x=B,` y=C.(9.14)
Der Wert von C wird aus den Gleichungen bestimmt:
Punkt (9.14) – Fokus (Abb.9.6 A) oder Knoten (Abb.9.6 G), deren Stabilität vom Vorzeichen der Größe abhängtS
S 2 = – k 1 (B) – k 1 (B)B+L(B)C.
Wenn S>0, Ein Punkt ist stabil, wennS<0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 B)
In der ausländischen Literatur wird häufiger ein ähnliches Modell von Rosenzweig und MacArthur (1963) berücksichtigt:
 (9.15)
(9.15)
Wo F(X) – Änderungsrate der Zahl der Opfer X in Abwesenheit von Raubtieren, F( x,y) - Intensität der Raubtiere, k- Koeffizient, der die Effizienz der Verarbeitung von Beutebiomasse in Raubtierbiomasse charakterisiert, e- Raubtiersterblichkeit.
Modell (9.15) reduziert sich unter folgenden Annahmen auf einen Spezialfall des Kolmogorov-Modells (9.12):
1) Die Anzahl der Raubtiere wird nur durch die Anzahl der Beute begrenzt.
2) Die Geschwindigkeit, mit der ein bestimmtes Raubtier Beute frisst, hängt nur von der Dichte der Beutepopulation ab und hängt nicht von der Dichte der Raubtierpopulation ab.
Dann nehmen die Gleichungen (9.15) die Form an.
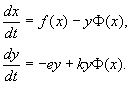
Bei der Beschreibung der Interaktion realer Arten werden die rechten Seiten der Gleichungen entsprechend den Vorstellungen über biologische Realitäten spezifiziert. Betrachten wir eines der beliebtesten Modelle dieser Art.
Modell der Interaktion zwischen zwei Arten von Insekten (MacArthur, 1971)
Das Modell, das wir im Folgenden betrachten werden, wurde verwendet, um das praktische Problem der Bekämpfung schädlicher Insekten durch Sterilisation der Männchen einer der Arten zu lösen. Basierend auf den biologischen Merkmalen der Arteninteraktion wurde das folgende Modell geschrieben
 (9.16)
(9.16)
Hier x,y- Biomasse von zwei Arten von Insekten. Die trophischen Interaktionen der in diesem Modell beschriebenen Arten sind sehr komplex. Dadurch wird die Form der Polynome auf der rechten Seite der Gleichungen bestimmt.
Schauen wir uns die rechte Seite der ersten Gleichung an. Insektenarten X fressen die Larven der Art bei(Mitglied +k 3 y), aber Erwachsene der Art bei fressen die Larven der Art X unterliegen einem hohen Artenreichtum X oder bei oder beide Typen (Mitglieder –k 4 xy, – y 2). Bei klein X Artensterblichkeit X höher als sein natürlicher Anstieg (1 –k 1 +k 2 x–x 2 < 0 bei klein X). In der zweiten Gleichung der Term k 5 spiegelt das natürliche Wachstum der Art wider y; –k 6 j – Selbstbeherrschung dieser Art,–k 7 X– Fressen von Larven der Art bei Insektenarten x, k 8 xy – Zunahme der Artenbiomasse bei aufgrund des Verzehrs dieser Art durch erwachsene Insekten bei Larven der Art X.
In Abb. 9.7 Es wird ein Grenzzyklus vorgestellt, der die Trajektorie einer stabilen periodischen Lösung des Systems darstellt (9.16).

Die Lösung der Frage, wie das Zusammenleben einer Population mit ihrer biologischen Umwelt sichergestellt werden kann, kann natürlich nicht ohne Berücksichtigung der Besonderheiten eines bestimmten biologischen Systems und einer Analyse aller seiner Wechselbeziehungen erfolgen. Gleichzeitig ermöglicht uns das Studium formaler mathematischer Modelle die Beantwortung einiger allgemeiner Fragen. Man kann argumentieren, dass bei Modellen wie (9.12) die Tatsache der Kompatibilität oder Inkompatibilität von Populationen nicht von ihrer ursprünglichen Größe abhängt, sondern nur durch die Art der Interaktion der Arten bestimmt wird. Das Modell hilft bei der Beantwortung der Frage: Wie kann man die Biozönose beeinflussen und steuern, um die schädlichen Arten schnellstmöglich zu vernichten?
Das Management kann auf eine kurzfristige, abrupte Änderung der Bevölkerungswerte reduziert werden X Und u. Diese Methode entspricht Bekämpfungsmethoden wie der einmaligen Zerstörung einer oder beider Populationen auf chemischem Wege. Aus der oben formulierten Aussage geht klar hervor, dass diese Kontrollmethode für kompatible Populationen unwirksam sein wird, da das System mit der Zeit wieder ein stationäres Regime erreichen wird.
Eine andere Möglichkeit besteht darin, die Art der Interaktionsfunktionen zwischen Ansichten zu ändern, beispielsweise beim Ändern der Werte von Systemparametern. Dieser parametrischen Methode entsprechen die biologischen Kontrollmethoden. Wenn also sterilisierte Männchen eingeführt werden, verringert sich die Rate des natürlichen Bevölkerungswachstums. Wenn wir gleichzeitig ein andersartiges Phasenbild erhalten, bei dem nur ein stabiler stationärer Zustand mit null Schädlingszahlen vorliegt, führt die Bekämpfung zum gewünschten Ergebnis – Zerstörung der Population einer schädlichen Art. Es ist interessant festzustellen, dass es manchmal ratsam ist, die Wirkung nicht auf den Schädling selbst, sondern auf seinen Partner auszuüben. Generell lässt sich nicht sagen, welche Methode effektiver ist. Dies hängt von den verfügbaren Kontrollen und von der expliziten Form der Funktionen ab, die die Interaktion von Populationen beschreiben.
Modell von A.D. Bazykin
Die theoretische Analyse von Modellen der Arteninteraktionen wurde am umfassendsten in A.D. Bazykins Buch „Biophysics of Interacting Populations“ (M., Nauka, 1985) durchgeführt.
Betrachten wir eines der in diesem Buch untersuchten Raubtier-Beute-Modelle.
 (9.17)
(9.17)
System (9.17) ist eine Verallgemeinerung des einfachsten Volterra-Raubtier-Beute-Modells (5.17) unter Berücksichtigung des Effekts der Raubtiersättigung. Modell (5.17) geht davon aus, dass die Intensität der Beutebeweidung linear mit zunehmender Beutedichte zunimmt, was bei hohen Beutedichten nicht der Realität entspricht. Zur Beschreibung der Abhängigkeit der Ernährung eines Raubtiers von der Beutedichte können verschiedene Funktionen gewählt werden. Es ist am wichtigsten, dass die gewählte Funktion mit dem Wachstum einhergeht X tendierte asymptotisch zu einem konstanten Wert. Modell (9.6) verwendete eine logistische Abhängigkeit. In Bazykins Modell wird die Hyperbel als solche Funktion gewählt X/(1+px). Erinnern wir uns daran, dass dies die Form der Monod-Formel ist, die die Abhängigkeit der Wachstumsrate von Mikroorganismen von der Konzentration des Substrats beschreibt. Dabei fungiert die Beute als Substrat und das Raubtier als Mikroorganismen. .
System (9.17) hängt von sieben Parametern ab. Die Anzahl der Parameter kann durch Ersetzen von Variablen reduziert werden:
X® (ANZEIGE)X; j ® (ANZEIGE)/y;
T® (1/A)T; g (9.18)
und hängt von vier Parametern ab.
Für eine vollständige qualitative Untersuchung ist es notwendig, den vierdimensionalen Parameterraum in Bereiche mit unterschiedlichem dynamischem Verhalten zu unterteilen, d.h. Erstellen Sie ein parametrisches oder strukturelles Porträt des Systems.
Anschließend ist es notwendig, für jeden Bereich des parametrischen Porträts Phasenporträts zu erstellen und die Verzweigungen zu beschreiben, die bei den Phasenporträts an den Grenzen verschiedener Bereiche des parametrischen Porträts auftreten.
Die Konstruktion eines vollständigen parametrischen Porträts erfolgt in Form einer Reihe von „Scheiben“ (Projektionen) eines niedrigdimensionalen parametrischen Porträts mit festen Werten einiger Parameter.
Parametrisches Porträt des Systems (9.18) für feste G und Klein e dargestellt in Abb. 9.8. Das Porträt enthält 10 Bereiche mit unterschiedlichem Verhalten von Phasentrajektorien.

Reis. 9.8.Parametrisches Porträt des Systems (9.18) für festG
und Klein e
Das Verhalten des Systems bei unterschiedlichen Parameterverhältnissen kann deutlich unterschiedlich sein (Abb. 9.9). Das System ermöglicht:
1) ein stabiles Gleichgewicht (Bereiche 1 und 5);
2) ein stabiler Grenzzyklus (Regionen 3 und 8);
3) zwei stabile Gleichgewichte (Region 2)
4) stabiler Grenzzyklus und instabiles Gleichgewicht darin (Regionen 6, 7, 9, 10)
5) stabiler Grenzzyklus und stabiles Gleichgewicht außerhalb davon (Bereich 4).
In den Parameterbereichen 7, 9, 10 wird der Anziehungsbereich des Gleichgewichts durch einen instabilen Grenzzyklus begrenzt, der innerhalb eines stabilen liegt. Die interessanteste Struktur ist das Phasenporträt, das dem Bereich 6 im parametrischen Porträt entspricht. Im Detail ist es in Abb. dargestellt. 9.10.

Der Anziehungsbereich des Gleichgewichts B 2 (schattiert) ist eine „Schnecke“, die sich vom instabilen Fokus B 1 dreht. Wenn bekannt ist, dass sich das System zum Anfangszeitpunkt in der Nähe von B 1 befand, kann beurteilt werden, ob die entsprechende Trajektorie das Gleichgewicht B 2 oder einen stabilen Grenzzyklus um die drei Gleichgewichtspunkte C (Sattel) erreichen wird ), B 1 und B 2 basierend auf probabilistischen Überlegungen.

Abb.9.10.Phasenporträt des Systems 9.18 für den parametrischen Bereich 6. Der Anziehungsbereich B 2 ist schattiert
In einem parametrischen Porträt(9.7) sind es 22 verschiedene Bifurkationsgrenzen, die sich bilden 7 verschiedene Arten von Gabelungen. Ihre Studie ermöglicht es uns, mögliche Arten des Systemverhaltens zu identifizieren, wenn sich seine Parameter ändern. Zum Beispiel beim Umzug aus der Gegend 1 bis Bereich 3 Es kommt zur Entstehung eines kleinen Grenzzyklus oder zur sanften Entstehung von Selbstschwingungen um ein einziges Gleichgewicht IN. Eine ähnliche sanfte Geburt von Selbstschwingungen, aber um eines der Gleichgewichte herum, nämlich B 1 , tritt auf, wenn die Grenzen von Regionen überschritten werden 2 und 4. Beim Verlassen des Geländes 4 bis Bereich 5 stabiler Grenzzyklus um einen PunktB 1 „platzt“ auf der Schleife der Separatoren und der einzige Anziehungspunkt bleibt das Gleichgewicht B 2 usw.
Von besonderem Interesse für die Praxis ist natürlich die Entwicklung von Kriterien für die Nähe eines Systems zu Bifurkationsgrenzen. Tatsächlich sind sich Biologen der „Pufferungs-“ oder „Flexibilitäts“-Eigenschaft natürlicher Ökosysteme durchaus bewusst. Unter diesen Begriffen versteht man üblicherweise die Fähigkeit eines Systems, äußere Einflüsse zu absorbieren. Solange die Intensität des äußeren Einflusses einen bestimmten kritischen Wert nicht überschreitet, erfährt das Verhalten des Systems keine qualitativen Veränderungen. Auf der Phasenebene entspricht dies der Rückkehr des Systems in einen stabilen Gleichgewichtszustand bzw. in einen stabilen Grenzzyklus, dessen Parameter sich nicht wesentlich vom ursprünglichen unterscheiden. Wenn die Intensität des Aufpralls das zulässige Maß überschreitet, „bricht“ das System zusammen und geht in ein qualitativ anderes dynamisches Verhalten über, es stirbt beispielsweise einfach ab. Dieses Phänomen entspricht einem Bifurkationsübergang.
Jede Art von Bifurkationsübergang weist ihre eigenen Besonderheiten auf, die es ermöglichen, die Gefahr eines solchen Übergangs für das Ökosystem einzuschätzen. Hier sind einige allgemeine Kriterien, die auf die Nähe einer gefährlichen Grenze hinweisen. Wie im Fall einer Art gilt: Wenn das System bei abnehmender Anzahl einer der Arten in der Nähe eines instabilen Sattelpunkts „stecken bleibt“, was sich in einer sehr langsamen Wiederherstellung der Anzahl auf den Anfangswert äußert, dann Das System befindet sich nahe der kritischen Grenze. Ein Indikator für Gefahr ist auch eine Veränderung der Form von Schwankungen in der Anzahl von Raubtieren und Beutetieren. Wenn aus harmonischen Schwingungen Relaxationsschwingungen werden und die Amplitude der Schwingungen zunimmt, kann dies zu einem Stabilitätsverlust des Systems und zum Aussterben einer der Arten führen.
Die weitere Vertiefung der mathematischen Theorie der Interaktion zwischen Arten geht dahin, die Struktur der Populationen selbst detailliert darzustellen und zeitliche und räumliche Faktoren zu berücksichtigen.
Literatur.
Kolmogorov A.N. Qualitative Untersuchung mathematischer Modelle der Bevölkerungsdynamik. // Probleme der Kybernetik. M., 1972, Heft 5.
MacArtur R. Grafische Analyse ökologischer Systeme // Bericht der Abteilung für Biologie der Perinceton University. 1971
A.D. Bazykin „Biophysik interagierender Populationen.“ M., Nauka, 1985.
V. Volterra: „Mathematische Theorie des Kampfes ums Dasein.“ M.. Wissenschaft, 1976
Gause G.F. Der Kampf ums Dasein. Baltimore, 1934.
Zurück in den 20er Jahren. A. Lotka und etwas später, unabhängig von ihm, V. Volterra schlugen mathematische Modelle vor, die konjugierte Schwankungen in den Populationen von Raubtieren und Beutetieren beschreiben. Betrachten wir die einfachste Version des Lotka-Volterra-Modells. Das Modell basiert auf einer Reihe von Annahmen:
1) Die Beutepopulation wächst in Abwesenheit eines Raubtiers exponentiell,
2) der Druck von Raubtieren hemmt dieses Wachstum,
3) Die Sterblichkeit der Beute ist proportional zur Häufigkeit der Begegnungen zwischen Raubtier und Beute (oder andernfalls proportional zum Produkt ihrer Populationsdichten);
4) Die Geburtenrate eines Raubtiers hängt von der Intensität des Beutekonsums ab.
Die momentane Änderungsrate der Beutepopulationsgröße kann durch die Gleichung ausgedrückt werden
dN f /dt = r 1 N f - p 1 N f N x,
wo r 1 - spezifische momentane Rate des Populationswachstums der Beute, p 1 – Konstante, die die Sterblichkeit der Beute mit der Dichte des Raubtiers verbindet, a N Und Nx - Dichte der Beute bzw. des Raubtiers.
Es wird angenommen, dass die momentane Wachstumsrate der Raubtierpopulation in diesem Modell der Differenz zwischen der Geburtenrate und der konstanten Sterblichkeit entspricht:
dN x /dt = p 2 N x N x – d 2 N x,
wo p 2 - Konstante, die die Geburtenrate in einer Raubtierpopulation mit der Beutedichte in Beziehung setzt, a d 2 - spezifische Sterblichkeitsrate des Raubtiers.
Gemäß den obigen Gleichungen wird jede der interagierenden Populationen in ihrem Wachstum nur durch die andere Population begrenzt, d. h. Der Anstieg der Zahl der Opfer wird durch den Druck der Raubtiere begrenzt, und der Anstieg der Zahl der Raubtiere wird durch die unzureichende Zahl der Opfer begrenzt. Es wird keine Selbstlimitierung der Populationen angenommen. Man geht beispielsweise davon aus, dass immer genug Nahrung für das Opfer vorhanden ist. Es ist auch nicht zu erwarten, dass die Beutepopulation der Kontrolle des Raubtiers entgeht, obwohl dies tatsächlich recht häufig vorkommt.
Trotz aller Konventionalität des Lotka-Volterra-Modells verdient es Aufmerksamkeit, schon allein deshalb, weil es zeigt, wie selbst ein solch idealisiertes System der Interaktion zwischen zwei Populationen zu einer recht komplexen Dynamik ihrer Zahlen führen kann. Die Lösung des Systems dieser Gleichungen ermöglicht es uns, die Bedingungen für die Aufrechterhaltung einer konstanten (Gleichgewichts-)Anzahl jeder Art zu formulieren. Die Beutepopulation bleibt konstant, wenn die Dichte des Raubtiers gleich r 1 /p 1 ist, und damit die Raubtierpopulation konstant bleibt, muss die Dichte der Beute gleich d 2 /p 2 sein. Tragen wir die Opferdichte auf der x-Achse ein N Und , und entlang der Ordinate - die Dichte des Raubtiers N X, dann sind die Isoklinen, die den Zustand der Konstanz von Raubtier und Beute zeigen, zwei gerade Linien, die senkrecht zueinander und zu den Koordinatenachsen stehen (Abb. 6,a). Es wird davon ausgegangen, dass unterhalb einer bestimmten Beutedichte (gleich d 2 /p 2) die Dichte des Raubtiers immer abnimmt und darüber immer zunimmt. Dementsprechend nimmt die Dichte der Beute zu, wenn die Dichte des Raubtiers unter dem Wert gleich r 1 / p 1 liegt, und nimmt ab, wenn sie über diesem Wert liegt. Der Schnittpunkt der Isoklinen entspricht der Bedingung einer konstanten Häufigkeit von Raubtieren und Beutetieren, und andere Punkte auf der Ebene dieses Diagramms bewegen sich entlang geschlossener Trajektorien und spiegeln somit regelmäßige Schwankungen in der Häufigkeit von Raubtieren und Beutetieren wider (Abb. 6, B). Der Schwingungsbereich wird durch das anfängliche Verhältnis der Dichten von Räuber und Beute bestimmt. Je näher es am Schnittpunkt der Isoklinen liegt, desto kleiner ist der durch die Vektoren beschriebene Kreis und desto kleiner ist dementsprechend die Amplitude der Schwingungen.
Reis. 6. Grafische Darstellung des Lotka-Voltaire-Modells für das Raubtier-Beute-System.
Einer der ersten Versuche, Schwankungen in der Häufigkeit von Raubtieren und Beutetieren in Laborexperimenten zu ermitteln, wurde von G.F. unternommen. Gause. Die Objekte dieser Experimente waren die Ciliaten Paramecium (Paramecium caudatum) und das räuberische Wimpertier Didinium (Didinium Nasutum). Die Nahrung für Paramecium war eine Suspension von Bakterien, die dem Medium regelmäßig zugesetzt wurde, und Didinium ernährte sich ausschließlich von Paramecium. Dieses System erwies sich als äußerst instabil: Der Druck des Raubtiers führte mit zunehmender Zahl zur vollständigen Ausrottung der Opfer, woraufhin die Population des Raubtiers selbst ausstarb. Um die Experimente zu erschweren, richtete Gause einen Unterschlupf für das Opfer ein, indem er ein wenig Glaswolle in Reagenzgläser mit Ciliaten einführte. Paramecia konnte sich frei zwischen den Wattefäden bewegen, Didinium jedoch nicht. In dieser Version des Experiments fraß Didinium alle Paramecia, die im wattefreien Teil des Reagenzglases schwammen, und starb aus, und die Paramecia-Population wurde dann durch die Fortpflanzung von Individuen, die im Tierheim überlebten, wiederhergestellt. Gause konnte nur dann einen gewissen Anschein von Schwankungen in der Anzahl von Raubtieren und Beutetieren erzielen, wenn er von Zeit zu Zeit sowohl Beute als auch Raubtiere in die Kultur einführte und so eine Einwanderung simulierte.
40 Jahre nach Gauses Arbeit wurden seine Experimente von L. Luckinbill wiederholt, der Ciliaten als Opfer verwendete Paramecium Aurelia, und als Raubtier desselben Didinium Nasutum. Luckinbill gelang es, mehrere Schwankungszyklen in der Zahl dieser Populationen zu erreichen, allerdings nur in dem Fall, in dem die Dichte des Parameciums durch einen Mangel an Nahrung (Bakterien) begrenzt war und der Kulturflüssigkeit Methylzellulose zugesetzt wurde – eine Substanz, die die Zahl reduziert Geschwindigkeit der Bewegung von Raubtier und Beute und verringert daher die Häufigkeit ihrer möglichen Begegnungen. Es stellte sich auch heraus, dass es einfacher ist, Schwingungen zwischen Räuber und Beute zu erreichen, wenn das Volumen des Versuchsgefäßes vergrößert wird, obwohl auch in diesem Fall die Bedingung einer Nahrungsbeschränkung der Beute erforderlich ist. Wenn dem System aus Raubtier und Beute, die in einem oszillierenden Modus nebeneinander existieren, überschüssige Nahrung hinzugefügt wurde, dann war die Reaktion ein rascher Anstieg der Zahl der Beute, gefolgt von einem Anstieg der Zahl der Raubtiere, was wiederum zur vollständigen Ausrottung von Raubtieren führte die Beutepopulation.
Die Lotka- und Volterra-Modelle dienten als Anstoß für die Entwicklung einer Reihe weiterer realistischerer Modelle des Raubtier-Beute-Systems. Insbesondere ein recht einfaches grafisches Modell, das das Verhältnis verschiedener Beute-Isoklinen analysiert Raubtier, wurde von M. Rosenzweig und R. MacArthur (Rosenzweig, MacArthur) vorgeschlagen. Laut diesen Autoren sind stationäre ( = konstant) Die Anzahl der Beute in den Koordinatenachsen der Dichte von Raubtier und Beute kann in Form einer konvexen Isokline dargestellt werden (Abb. 7, a). Ein Punkt, an dem sich die Isokline mit der Beutedichtelinie schneidet, entspricht der minimal zulässigen Beutedichte (die Bevölkerung darunter ist einem sehr hohen Risiko des Aussterbens ausgesetzt, allein schon aufgrund der geringen Häufigkeit von Treffen zwischen Männern und Frauen), und der andere Punkt entspricht dem Maximum, bestimmt durch die Menge der verfügbaren Nahrung oder die Verhaltensmerkmale der Beute selbst. Wir möchten betonen, dass wir immer noch über minimale und maximale Dichten in Abwesenheit eines Raubtiers sprechen. Wenn ein Raubtier auftaucht und seine Zahl zunimmt, sollte die minimal zulässige Beutedichte natürlich höher und die maximale niedriger sein. Jeder Wert der Beutedichte muss einer bestimmten Räuberdichte entsprechen, bei der eine Konstanz der Beutepopulation erreicht wird. Die geometrische Lage solcher Punkte ist die Beute-Isokline in den Dichtekoordinaten von Räuber und Beute. Vektoren, die die Richtung der Änderung der Beutedichte (horizontal ausgerichtet) zeigen, haben auf verschiedenen Seiten der Isokline unterschiedliche Richtungen (Abb. 7a).

Reis. 7. Isokline stationärer Populationen von Beutetieren (a) und Raubtieren (b).
Für das Raubtier wurde ebenfalls eine Isokline in denselben Koordinaten konstruiert, die dem stationären Zustand seiner Population entspricht. Vektoren, die die Richtung der Änderung der Raubtierhäufigkeit anzeigen, sind nach oben oder unten ausgerichtet, je nachdem, auf welcher Seite der Isokline sie sich befinden. Die Form der Raubtier-Isokline, dargestellt in Abb. 7, B. wird erstens durch das Vorhandensein einer bestimmten Mindestdichte der Beute bestimmt, die ausreicht, um die Population des Raubtiers aufrechtzuerhalten (bei einer geringeren Dichte der Beute kann das Raubtier seine Zahl nicht erhöhen), und zweitens durch das Vorhandensein von a bestimmte maximale Dichte des Raubtiers selbst, oberhalb derer die Zahl unabhängig von der Häufigkeit der Opfer abnimmt.

Reis. 8. Die Entstehung von Oszillationsmodi im Räuber-Beute-System in Abhängigkeit vom Standort des Räubers und der Isoklinen der Beute.
Bei der Kombination von Beute- und Raubtier-Isoklinen in einem Diagramm sind drei verschiedene Optionen möglich (Abb. 8). Wenn die Räuber-Isokline die Beute-Isokline an der Stelle schneidet, an der sie bereits abnimmt (bei hoher Beutedichte), bilden die Vektoren, die Änderungen in der Häufigkeit von Räuber und Beute zeigen, eine nach innen gedrehte Flugbahn, was gedämpften Fluktuationen in der Häufigkeit entspricht von Beute und Raubtier (Abb. 8, A). Für den Fall, dass die Isokline des Raubtiers die Isokline der Beute in ihrem aufsteigenden Teil schneidet (d. h. im Bereich niedriger Werte der Beutedichte), bilden die Vektoren eine sich abwickelnde Flugbahn, und mit zunehmender Zunahme treten Schwankungen in der Anzahl der Raubtiere und Beute auf Amplitude bzw. (Abb. 8, B). Wenn die Isokline des Raubtiers die Isokline der Beute im Bereich ihrer Spitze schneidet, bilden die Vektoren einen geschlossenen Kreis und Schwankungen in der Anzahl der Beute und des Raubtiers sind durch eine stabile Amplitude und Periode gekennzeichnet (Abb. 8, V).
Mit anderen Worten entsprechen gedämpfte Schwingungen einer Situation, in der ein Raubtier einen spürbaren Einfluss auf eine Beutepopulation ausübt, die nur eine sehr hohe Dichte (nahe dem Maximum) erreicht hat, und es treten Schwingungen mit zunehmender Amplitude auf, wenn das Raubtier dazu in der Lage ist Auch bei geringer Beutedichte lässt sich seine Zahl schnell erhöhen und so schnell vernichten. In anderen Versionen ihres Modells zeigten Posenzweig und McArthur, dass Räuber-Beute-Oszillationen durch die Einführung eines „Zufluchtsorts“, d. h. Dies deutet darauf hin, dass es in einem Gebiet mit geringer Beutedichte ein Gebiet gibt, in dem die Beutehäufigkeit unabhängig von der Anzahl der vorhandenen Raubtiere zunimmt.
Der Wunsch, Modelle durch Erhöhung ihrer Komplexität realistischer zu machen, manifestierte sich nicht nur in den Werken von Theoretikern, sondern auch Experimentatoren. Interessante Ergebnisse erzielte insbesondere Huffaker, der am Beispiel einer kleinen pflanzenfressenden Milbe die Möglichkeit der Koexistenz von Räuber und Beute im Oszillationsmodus aufzeigte Eotetranychus Sexmaculatus und eine räuberische Zecke greift ihn an Typhlodromus occidentalis. Als Nahrung für die pflanzenfressende Milbe dienten Orangen auf Tabletts mit Löchern (wie sie zum Aufbewahren und Transportieren von Eiern verwendet werden). Die Originalversion enthielt 40 Löcher auf einem Tablett, von denen einige Orangen (teilweise geschält) und andere Gummibälle enthielten. Beide Zeckenarten vermehren sich parthenogenetisch sehr schnell, sodass die Art ihrer Populationsdynamik in relativ kurzer Zeit aufgedeckt werden kann. Nachdem er 20 Weibchen der pflanzenfressenden Milbe auf ein Tablett gelegt hatte, beobachtete Huffaker das schnelle Wachstum seiner Population, die sich auf dem Niveau von 5-8.000 Individuen (pro Orange) stabilisierte. Fügte man der wachsenden Beutepopulation mehrere Individuen eines Raubtiers hinzu, vergrößerte sich die Beutepopulation schnell und starb aus, als alle Opfer gefressen waren.
Durch die Vergrößerung der Schale auf 120 Löcher, in denen einzelne Orangen zufällig auf viele Gummibälle verteilt waren, konnte Huffaker die Koexistenz von Raubtier und Beute verlängern. Wie sich herausstellte, spielt das Verhältnis ihrer Ausbreitungsraten eine wichtige Rolle bei der Interaktion zwischen Räuber und Beute. Huffaker schlug vor, dass durch die Erleichterung der Bewegung der Beute und die Erschwerung der Bewegung des Raubtiers die Zeit ihres Zusammenlebens verlängert werden könnte. Dazu wurden auf einem Tablett mit 120 Löchern 6 Orangen zufällig zwischen Gummibällen platziert, und um die Löcher mit Orangen wurden Vaseline-Barrieren gebaut, um die Ausbreitung des Raubtiers zu verhindern, und um die Ansiedlung der Beute zu erleichtern, wurden Holzpflöcke angebracht auf dem Tablett befestigt und dienen als eine Art „Startrampe“ für pflanzenfressende Milben (Tatsache ist, dass diese Art dünne Fäden produziert und mit deren Hilfe in der Luft schweben und sich mit dem Wind ausbreiten kann). In einem solch komplexen Lebensraum existierten Räuber und Beute acht Monate lang nebeneinander, was drei vollständige Zyklen von Populationsschwankungen zeigt. Die wichtigsten Bedingungen für dieses Zusammenleben sind folgende: Heterogenität des Lebensraums (im Sinne des Vorhandenseins geeigneter und ungeeigneter Gebiete für das Leben von Beutetieren) sowie die Möglichkeit der Migration von Beutetieren und Raubtieren (unter Beibehaltung). ein gewisser Vorteil der Beute in der Geschwindigkeit dieses Prozesses). Mit anderen Worten, ein Raubtier kann die eine oder andere lokale Ansammlung von Beutetieren vollständig ausrotten, aber einige der Beutetiere haben Zeit, zu wandern und andere lokale Ansammlungen zu bilden. Früher oder später wird das Raubtier auch neue lokale Ansammlungen erreichen, aber in der Zwischenzeit wird die Beute Zeit haben, sich an anderen Orten niederzulassen (auch dort, wo sie zuvor lebte, dann aber ausgerottet wurde).
Ähnliches wie Huffaker im Experiment beobachtete, passiert auch unter natürlichen Bedingungen. Zum Beispiel der Kaktusmotten-Schmetterling (Cactoblastis cactorum), Nach Australien gebracht, reduzierte sich die Anzahl der Feigenkakteen erheblich, vernichtete sie jedoch nicht vollständig, gerade weil sich der Kaktus etwas schneller ausbreiten konnte. An Orten, an denen der Feigenkaktus vollständig ausgerottet ist, kommt der Motte nicht mehr vor. Wenn der Feigenkaktus also nach einiger Zeit wieder hier eindringt, kann er eine gewisse Zeit lang wachsen, ohne dass die Gefahr besteht, dass er von der Motte zerstört wird. Mit der Zeit taucht die Motte hier jedoch erneut auf und vernichtet durch schnelle Vermehrung den Feigenkaktus.
Wenn man über Raubtier-Beute-Schwankungen spricht, kann man nicht umhin, die zyklischen Veränderungen in der Anzahl der Hasen und Luchse in Kanada zu erwähnen, die auf der Grundlage der Statistiken über die Pelzjagd der Hudson Bay Company vom Ende des 18. Jahrhunderts bis zum Beginn des 20. Jahrhunderts verfolgt werden 20. Jahrhundert. Dieses Beispiel wurde oft als klassische Veranschaulichung der Schwankungen zwischen Raubtier und Beute angesehen, obwohl wir in Wirklichkeit nur das Populationswachstum des Raubtiers (Luchs) im Anschluss an das Wachstum der Beutepopulation (Hase) sehen. Der Rückgang der Hasenzahl nach jedem Anstieg konnte nicht nur durch den erhöhten Druck von Raubtieren erklärt werden, sondern hing mit anderen Faktoren zusammen, offenbar vor allem mit dem Nahrungsmangel im Winter. Zu dieser Schlussfolgerung kam insbesondere M. Gilpin, der zu prüfen versuchte, ob diese Daten durch das klassische Lotka-Volterra-Modell beschrieben werden können. Die Testergebnisse zeigten, dass es keine zufriedenstellende Anpassung an das Modell gab, aber seltsamerweise wurde es besser, wenn Raubtier und Beute getauscht wurden, d. h. interpretierte den Luchs als „Beute“ und den Hasen als „Raubtier“. Eine ähnliche Situation spiegelt sich im humorvollen Titel des Artikels wider („Fressen Hasen Luchse?“), der im Wesentlichen sehr ernst ist und in einer seriösen wissenschaftlichen Zeitschrift veröffentlicht wurde.
das PA88-System, das anhand seiner Strukturformel gleichzeitig die Wahrscheinlichkeit von mehr als 100 pharmakologischen Wirkungen und Wirkmechanismen eines Stoffes vorhersagt. Die Wirksamkeit dieses Ansatzes zur Planung des Screenings liegt bei etwa 800 %, und die Genauigkeit der Computervorhersage ist 300 % höher als die Vorhersage von Experten.
Eines der konstruktiven Werkzeuge zur Gewinnung neuer Erkenntnisse und Lösungen in der Medizin ist daher die Methode der mathematischen Modellierung. Der Prozess der Mathematisierung der Medizin ist ein häufiger Ausdruck der Durchdringung wissenschaftlicher Erkenntnisse und steigert die Effizienz der Behandlung und der Präventionsarbeit.
4. Mathematisches Modell „Raubtier-Beute“
Zum ersten Mal in der Biologie wurde vom italienischen Mathematiker V. Volterra und seinen Kollegen ein mathematisches Modell periodischer Veränderungen in der Anzahl antagonistischer Tierarten vorgeschlagen. Das von Volterra vorgeschlagene Modell war eine Weiterentwicklung der Idee, die A. Lottka 1924 im Buch „Elements of Physical Biology“ dargelegt hatte. Daher ist dieses klassische mathematische Modell als „Lottky-Volterra“-Modell bekannt.
Obwohl die Beziehungen antagonistischer Arten in der Natur komplexer sind als in einem Modell, sind sie dennoch ein gutes Lehrmodell, an dem sich die Grundideen der mathematischen Modellierung erlernen lassen.
Das Problem also: In einem ökologisch geschlossenen Gebiet leben zwei Tierarten (z. B. Luchse und Hasen). Hasen (Beutetiere) ernähren sich von pflanzlicher Nahrung, die immer in ausreichender Menge verfügbar ist (dieses Modell berücksichtigt nicht die begrenzten Ressourcen pflanzlicher Nahrung). Luchse (Raubtiere) können nur Hasen fressen. Es muss ermittelt werden, wie sich die Anzahl der Beutetiere und Raubtiere in einem solchen Ökosystem im Laufe der Zeit verändert. Wenn die Beutetierpopulation zunimmt, steigt die Wahrscheinlichkeit von Begegnungen zwischen Räubern und Beutetieren, und dementsprechend nimmt mit einer gewissen Zeitverzögerung die Beutetierpopulation zu. Dieses recht einfache Modell beschreibt die Interaktion zwischen realen Raubtier- und Beutepopulationen in der Natur recht angemessen.
Jetzt fangen wir an Differentialgleichungen aufstellen. Um
Bezeichnen wir die Anzahl der Beutetiere mit N und die Anzahl der Raubtiere mit M. Die Zahlen N und M sind Funktionen der Zeit t. In unserem Modell berücksichtigen wir folgende Faktoren:
a) natürliche Fortpflanzung der Opfer; b) natürlicher Tod der Opfer;
c) Zerstörung von Opfern durch Fressen durch Raubtiere; d) natürliches Aussterben von Raubtieren;
e) eine Zunahme der Zahl der Raubtiere aufgrund der Fortpflanzung in Gegenwart von Nahrung.
Da es sich um ein mathematisches Modell handelt, besteht die Aufgabe darin, Gleichungen zu erhalten, die alle vorgesehenen Faktoren einbeziehen und die Dynamik beschreiben, also die Veränderung der Anzahl der Raubtiere und Beutetiere im Laufe der Zeit.
Die Anzahl der Beutetiere und Raubtiere soll sich im Laufe der Zeit t um ∆N und ∆M ändern. Die Veränderung der Opferzahl ∆N über die Zeit ∆t wird zum einen durch die Zunahme infolge der natürlichen Fortpflanzung (die proportional zur verfügbaren Opferzahl ist) bestimmt:
wobei B der Proportionalitätskoeffizient ist, der die Rate des natürlichen Aussterbens der Opfer charakterisiert.
Die Grundlage für die Ableitung einer Gleichung, die den Rückgang der Beutezahl aufgrund des Fressens durch Raubtiere beschreibt, ist die Idee, dass die Beutezahl umso schneller abnimmt, je häufiger sie angetroffen werden. Es ist auch klar, dass die Häufigkeit der Begegnungen zwischen Raubtieren und Beutetieren proportional sowohl zur Anzahl der Opfer als auch zur Anzahl der Raubtiere ist
Wenn wir die linke und rechte Seite der Gleichung (4) durch ∆t dividieren und zum Grenzwert bei ∆t→0 übergehen, erhalten wir Differentialgleichung erste Bestellung:
Um diese Gleichung zu lösen, müssen Sie wissen, wie sich die Anzahl der Raubtiere (M) im Laufe der Zeit ändert. Die Veränderung der Anzahl der Raubtiere (∆M) wird durch einen Anstieg aufgrund der natürlichen Fortpflanzung bei Vorhandensein ausreichender Nahrung (M 1 = Q∙N∙M∙∆t) und einen Rückgang aufgrund des natürlichen Aussterbens von Raubtieren ( M 2 = - P∙M∙∆ t):
M = Q∙N∙M∙∆t - P∙M∙∆t |
Aus Gleichung (6) können wir die Differentialgleichung erhalten:
Die Differentialgleichungen (5) und (7) stellen ein mathematisches „Raubtier-Beute“-Modell dar. Es reicht aus, die Werte des Koeffizienten zu bestimmen

Zur Lösung des Problems können die Entitäten A, B, C, Q, P und ein mathematisches Modell verwendet werden.
Überprüfung und Anpassung des mathematischen Modells. In diesem Labor
Neben der Berechnung des vollständigsten mathematischen Modells (Gleichungen 5 und 7) wird vorgeschlagen, einfachere Modelle zu untersuchen, bei denen etwas nicht berücksichtigt wird.
Nachdem Sie die fünf Komplexitätsebenen des mathematischen Modells betrachtet haben, können Sie die Phase der Überprüfung und Anpassung des Modells „fühlen“.
1. Ebene – im Modell wird für „Beute“ nur deren natürliche Fortpflanzung berücksichtigt, es gibt keine „Raubtiere“;
Stufe 2 – das Modell berücksichtigt das natürliche Aussterben von „Beutetieren“, es gibt keine „Raubtiere“;
Stufe 3 – das Modell berücksichtigt die natürliche Fortpflanzung von „Opfern“
Und Aussterben, keine „Raubtiere“;
4. Ebene – das Modell berücksichtigt die natürliche Fortpflanzung von „Opfern“
Und vom Aussterben bedroht und von „Raubtieren“ gefressen, die Zahl der „Raubtiere“ bleibt jedoch unverändert;
Stufe 5 – das Modell berücksichtigt alle besprochenen Faktoren.
Wir haben also das folgende Differentialgleichungssystem:
wobei M die Anzahl der „Raubtiere“ ist; N – Anzahl der „Opfer“;
t – aktuelle Zeit;
A – Reproduktionsrate von „Opfern“; C – Häufigkeit von Räuber-Beute-Begegnungen; B – Aussterberate der „Opfer“;
Q – Fortpflanzung von „Raubtieren“;
P – Aussterben der „Raubtiere“.
1. Ebene: M = 0, B = 0; 2. Ebene: M = 0, A = 0; 3. Ebene: M = 0; 4. Ebene: Q = 0, P = 0;
Level 5: vollständiges Gleichungssystem.
Wenn wir die Werte der Koeffizienten in jede Ebene einsetzen, erhalten wir unterschiedliche Lösungen, zum Beispiel:
Für die 3. Ebene ist der Wert des Koeffizienten M=0

Lösen der Gleichung, die wir erhalten
Ebenso für Level 1 und 2. Für die 4. und 5. Ebene ist es hier erforderlich, das Gleichungssystem mit der Runge-Kutta-Methode zu lösen. Als Ergebnis erhalten wir eine Lösung für mathematische Modelle dieser Ebenen.
II. ARBEITEN DER SCHÜLER WÄHREND DES PRAKTISCHEN UNTERRICHTS
Übung 1 . Mündliche Sprachkontrolle und Korrektur der Beherrschung des theoretischen Unterrichtsstoffs. Bestehen der Zulassung zum Unterricht.
Aufgabe 2. Durchführung von Laborarbeiten, Besprechung der erzielten Ergebnisse, Verfassen von Notizen.
Abschluss der Arbeiten
1. Rufen Sie vom Computer-Desktop aus das Programm „Lab. Nr. 6“ auf, indem Sie mit der linken Maustaste auf die entsprechende Verknüpfung doppelklicken.
2. Doppelklicken Sie mit der linken Maustaste auf die Verknüpfung „PREDATOR“.
3. Wählen Sie die Verknüpfung „PRED“ und wiederholen Sie den Programmaufruf mit der linken Maustaste (durch Doppelklick).
4. Drücken Sie nach dem Titelbildschirm „ENTER“.
5. Das Modellieren beginnt mit 1. Ebene.
6. Geben Sie das Jahr ein, ab dem das Modell analysiert werden soll: zum Beispiel 2000
7. Wählen Sie Zeitintervalle aus, zum Beispiel innerhalb von 40 Jahren, nach 1 Jahr (dann nach 4 Jahren).
2. Stufe: B = 0,05; N0 = 200;
3. Ebene: A = 0,02; B = 0,05; N = 200;
4. Stufe: A = 0,01; B = 0,002; C = 0,01; N0 = 200; M = 40; 5. Ebene: A = 1; B = 0,5; C = 0,02; Q = 0,002; P = 0,3; N0 = 200;
9. Erstellen Sie einen schriftlichen Bericht über die Arbeit, der Gleichungen, Diagramme, Ergebnisse der Berechnung der Eigenschaften des Modells und Schlussfolgerungen über die geleistete Arbeit enthalten sollte.
Aufgabe 3. Überwachung des endgültigen Wissensstandes:
a) ein mündlicher Bericht über die durchgeführten Laborarbeiten; b) Lösung situativer Probleme; c) Computertests.
Aufgabe 4. Aufgabe für die nächste Lektion: Abschnitt und Thema der Lektion, Abstimmung der Themen für Zusammenfassungsberichte (Berichtslänge 2-3 Seiten, Zeitvorgabe 5-7 Minuten).
Bundesamt für Bildung
Staatliche Bildungseinrichtung
höhere Berufsausbildung
„Staatliche Technische Universität Ischewsk“
Fakultät für Angewandte Mathematik
Abteilung „Mathematische Modellierung von Prozessen und Technologien“
Kursarbeit
in der Disziplin „Differentialgleichungen“
Thema: „Qualitative Erforschung des Räuber-Beute-Modells“
Ischewsk 2010
EINFÜHRUNG
1. PARAMETER UND GRUNDGLEICHUNG DES „RABIER-OPFER“-MODELLS
2.2 Verallgemeinerte Voltaire-Modelle vom Typ „Raubtier-Beute“.
3. PRAKTISCHE ANWENDUNG DES „RABIER-OPFER“-MODELLS
ABSCHLUSS
REFERENZLISTE
EINFÜHRUNG
Derzeit sind Umweltthemen von größter Bedeutung. Ein wichtiger Schritt zur Lösung dieser Probleme ist die Entwicklung mathematischer Modelle ökologischer Systeme.
Eine der Hauptaufgaben der Ökologie in der gegenwärtigen Phase ist die Untersuchung der Struktur und Funktionsweise natürlicher Systeme sowie die Suche nach allgemeinen Mustern. Die Mathematik hatte großen Einfluss auf die Ökologie und trug zur Entstehung der mathematischen Ökologie bei, insbesondere zu Abschnitten wie der Theorie der Differentialgleichungen, der Stabilitätstheorie und der Theorie der optimalen Kontrolle.
Eine der ersten Arbeiten auf dem Gebiet der mathematischen Ökologie war die Arbeit von A.D. Lotki (1880 - 1949), der als erster das Zusammenspiel verschiedener Populationen beschrieb, die durch Räuber-Beute-Beziehungen verbunden sind. Große Beiträge zur Erforschung des Raubtier-Beute-Modells leisteten V. Volterra (1860 - 1940), V.A. Kostitsin (1883-1963) Gegenwärtig werden die Gleichungen, die die Interaktion von Populationen beschreiben, Lotka-Volterra-Gleichungen genannt.
Die Lotka-Volterra-Gleichungen beschreiben die Dynamik der Durchschnittswerte – Bevölkerungsgröße. Derzeit wurden auf ihrer Grundlage allgemeinere Modelle der Populationsinteraktion erstellt, die durch Integro-Differentialgleichungen beschrieben werden, und kontrollierte Räuber-Beute-Modelle werden untersucht.
Eines der wichtigen Probleme der mathematischen Ökologie ist das Problem der Stabilität von Ökosystemen und des Managements dieser Systeme. Das Management kann mit dem Ziel durchgeführt werden, ein System zum Zweck seiner Nutzung oder Wiederherstellung von einem stabilen Zustand in einen anderen zu überführen.
1. PARAMETER UND GRUNDGLEICHUNG DES PREDATOR-PRIMATEN-MODELLS
Versuche, die Dynamik sowohl einzelner biologischer Populationen als auch von Gemeinschaften einschließlich interagierender Populationen mathematisch zu modellieren verschiedene Arten, werden seit langem durchgeführt. Eines der ersten Modelle des isolierten Bevölkerungswachstums (2.1) wurde bereits 1798 von Thomas Malthus vorgeschlagen:
, (1.1)Dieses Modell wird durch die folgenden Parameter spezifiziert:
N – Bevölkerungsgröße;
- die Differenz zwischen Geburten- und Sterberate.Wenn wir diese Gleichung integrieren, erhalten wir:
, (1.2)wobei N(0) die Populationsgröße zum Zeitpunkt t = 0 ist. Offensichtlich ist das Malthus-Modell bei
> 0 führt zu einem unendlichen Anstieg der Zahlen, der in natürlichen Populationen nie beobachtet wird, wo die Ressourcen, die dieses Wachstum gewährleisten, immer begrenzt sind. Veränderungen in der Anzahl der Populationen von Flora und Fauna können nicht durch ein einfaches malthusianisches Gesetz beschrieben werden; die Wachstumsdynamik wird durch viele miteinander verbundene Gründe beeinflusst – insbesondere reguliert und verändert sich die Fortpflanzung jeder Art selbst, so dass diese Art dabei erhalten bleibt der Evolution.Mathematische Beschreibung Mit diesen Gesetzen befasst sich die mathematische Ökologie – die Wissenschaft von den Beziehungen pflanzlicher und tierischer Organismen und der Gemeinschaften, die sie untereinander und mit ihnen bilden Umfeld.
Die ernsthafteste Untersuchung von Modellen biologischer Gemeinschaften, darunter mehrere Populationen verschiedener Arten, wurde vom italienischen Mathematiker Vito Volterra durchgeführt:
, - Einwohnerzahl; - Koeffizienten des natürlichen Wachstums (oder der Sterblichkeit) der Bevölkerung; - Koeffizienten der interspezifischen Interaktion. Abhängig von der Wahl der Koeffizienten beschreibt das Modell entweder den Kampf der Arten um gemeinsame Ressource oder Räuber-Beute-Interaktion, wenn eine Art Nahrung für eine andere ist. Während sich die Arbeiten anderer Autoren auf die Konstruktion verschiedener Modelle konzentrierten, führte V. Volterra eine eingehende Untersuchung der konstruierten Modelle biologischer Gemeinschaften durch. Mit dem Buch von V. Volterra begann nach Ansicht vieler Wissenschaftler die moderne mathematische Ökologie.2. QUALITATIVE FORSCHUNG DES ELEMENTÄREN „RÄUBIER-OPFER“-MODELLS
2.1 Modell der trophischen Interaktion nach dem Typ „Raubtier-Beute“.
Betrachten wir das von V. Volterre erstellte Modell der trophischen Interaktion vom Typ „Raubtier-Beute“. Es soll ein System aus zwei Arten geben, von denen die eine die andere frisst.
Betrachten wir den Fall, dass eine der Arten ein Raubtier und die andere eine Beute ist, und wir gehen davon aus, dass sich das Raubtier nur von der Beute ernährt. Nehmen wir die folgende einfache Hypothese an:
- Wachstumsrate des Opfers; - Wachstumsrate des Raubtiers; - Populationsgröße der Beute; - Populationsgröße des Raubtiers; - natürlicher Wachstumskoeffizient des Opfers; - Rate des Beuteverbrauchs durch ein Raubtier; - Sterblichkeitsrate des Raubtiers ohne Beute; - der Koeffizient der „Verarbeitung“ der Biomasse der Beute durch das Raubtier in seine eigene Biomasse.Anschließend wird die Populationsdynamik im Räuber-Beute-System durch ein System von Differentialgleichungen (2.1) beschrieben:
(2.1)wobei alle Koeffizienten positiv und konstant sind.
Das Modell hat eine Gleichgewichtslösung (2.2):
(2.2)Nach Modell (2.1) wird der Anteil der Raubtiere an der Gesamtmasse der Tiere durch Formel (2.3) ausgedrückt:
(2.3)Eine Analyse der Stabilität des Gleichgewichtszustandes gegenüber kleinen Störungen ergab, dass der singuläre Punkt (2.2) „neutral“ stabil (vom Typ „Zentrum“) ist, d. h. etwaige Abweichungen vom Gleichgewicht verschwinden nicht, sondern übertragen die versetzt das System in einen Schwingungsmodus mit einer Amplitude, die von der Größe der Störung abhängt. Systemtrajektorien auf der Phasenebene
haben die Form geschlossener Kurven, die in unterschiedlichen Abständen vom Gleichgewichtspunkt liegen (Abb. 1).Reis. 1 – Phase „Porträt“ des klassischen Volterra-Systems „Raubtier-Beute“
Wenn wir die erste Gleichung des Systems (2.1) durch die zweite dividieren, erhalten wir die Differentialgleichung (2.4) für die Kurve auf der Phasenebene
. (2.4)Wenn wir diese Gleichung integrieren, erhalten wir:
(2.5) ist die Integrationskonstante, wobeiEs lässt sich leicht zeigen, dass die Bewegung eines Punktes entlang der Phasenebene nur in eine Richtung erfolgt. Hierzu ist es sinnvoll, Funktionen auszutauschen
und , Verschieben des Koordinatenursprungs auf der Ebene zu einem stationären Punkt (2.2) und anschließendes Einführen von Polarkoordinaten: (2.6)In diesem Fall erhalten wir, wenn wir die Werte von System (2.6) in System (2.1) einsetzen.




