Logarithmen mit der gleichen Basisformel dividieren. Was ist ein Logarithmus? Logarithmen lösen. Beispiele. Eigenschaften von Logarithmen

Eines der Elemente der Algebra auf primitiver Ebene ist der Logarithmus. Der Name kommt aus dem Griechischen und leitet sich vom Wort „Zahl“ oder „Potenz“ ab und bedeutet die Potenz, mit der die Zahl in der Basis erhöht werden muss, um die endgültige Zahl zu finden.

Arten von Logarithmen

• log a b – Logarithmus der Zahl b zur Basis a (a > 0, a ≠ 1, b > 0);
• log b – dezimaler Logarithmus (Logarithmus zur Basis 10, a = 10);
• ln b – natürlicher Logarithmus (Logarithmus zur Basis e, a = e).

Wie löst man Logarithmen?

Der Logarithmus von b zur Basis a ist ein Exponent, der erfordert, dass b zur Basis a erhöht wird. Das erhaltene Ergebnis wird wie folgt ausgesprochen: „Logarithmus von b zur Basis a“. Die Lösung für logarithmische Probleme besteht darin, dass Sie die gegebene Potenz in Zahlen aus den angegebenen Zahlen bestimmen müssen. Es gibt einige Grundregeln, um den Logarithmus zu bestimmen oder zu lösen sowie die Notation selbst umzuwandeln. Mit ihnen werden logarithmische Gleichungen gelöst, Ableitungen gefunden, Integrale gelöst und viele andere Operationen ausgeführt. Im Grunde ist die Lösung des Logarithmus selbst seine vereinfachte Schreibweise. Nachfolgend sind die grundlegenden Formeln und Eigenschaften aufgeführt:

Für jedes a ; a > 0; a ≠ 1 und für jedes x ; y > 0.

• a log a b = b – einfach logarithmische Identität
• log a 1 = 0
• loga a = 1
• log a (x y) = log a x + log a y
• log a x/ y = log a x – log a y
• log a 1/x = -log a x
• log a x p = p log a x
• log a k x = 1/k log a x , für k ≠ 0
• log a x = log a c x c
• log a x = log b x/ log b a – Formel für den Umzug zu einer neuen Basis
• log a x = 1/log x a

So lösen Sie Logarithmen – Schritt-für-Schritt-Lösungsanleitung

• Schreiben Sie zunächst die erforderliche Gleichung auf.

Bitte beachten Sie: Wenn der Basislogarithmus 10 beträgt, wird die Eingabe gekürzt, sodass ein dezimaler Logarithmus entsteht. Wenn es eine natürliche Zahl e gibt, schreiben wir sie auf und reduzieren sie auf einen natürlichen Logarithmus. Das bedeutet, dass das Ergebnis aller Logarithmen die Potenz ist, mit der die Basiszahl erhöht wird, um die Zahl b zu erhalten.

Die Lösung liegt direkt in der Berechnung dieses Grades. Bevor ein Ausdruck mit einem Logarithmus gelöst wird, muss er nach der Regel, also mit Formeln, vereinfacht werden. Die wichtigsten Identitäten finden Sie, wenn Sie im Artikel etwas zurückgehen.

Addieren und Subtrahieren von Logarithmen mit zwei verschiedenen Zahlen, aber mit aus den gleichen Gründen, ersetzen Sie durch einen Logarithmus mit dem Produkt oder der Division der Zahlen b bzw. c. In diesem Fall können Sie die Formel für den Umzug zu einem anderen Stützpunkt anwenden (siehe oben).

Wenn Sie Ausdrücke zur Vereinfachung eines Logarithmus verwenden, müssen Sie einige Einschränkungen berücksichtigen. Und das heißt: Die Basis des Logarithmus a ist nur eine positive Zahl, aber nicht gleich Eins. Die Zahl b muss wie a größer als Null sein.

Es gibt Fälle, in denen Sie durch Vereinfachen eines Ausdrucks den Logarithmus nicht numerisch berechnen können. Es kommt vor, dass ein solcher Ausdruck keinen Sinn ergibt, weil viele Potenzen irrationale Zahlen sind. Belassen Sie unter dieser Bedingung die Potenz der Zahl als Logarithmus.

Logarithmische Ausdrücke, Lösungsbeispiele. In diesem Artikel werden wir uns mit Problemen im Zusammenhang mit der Lösung von Logarithmen befassen. Bei den Aufgaben geht es darum, die Bedeutung eines Ausdrucks herauszufinden. Es ist zu beachten, dass das Konzept des Logarithmus in vielen Aufgaben verwendet wird und es äußerst wichtig ist, seine Bedeutung zu verstehen. Was das Einheitliche Staatsexamen betrifft, wird der Logarithmus beim Lösen von Gleichungen, bei angewandten Problemen und auch bei Aufgaben im Zusammenhang mit dem Studium von Funktionen verwendet.

Lassen Sie uns Beispiele geben, um die eigentliche Bedeutung des Logarithmus zu verstehen:

Grundlegende logarithmische Identität:

Eigenschaften von Logarithmen, die man sich immer merken muss:

*Logarithmus des Produkts gleich der Summe Logarithmen von Faktoren.

* * *

*Der Logarithmus eines Quotienten (Bruch) ist gleich der Differenz zwischen den Logarithmen der Faktoren.

* * *

*Der Logarithmus eines Exponenten ist gleich dem Produkt aus dem Exponenten und dem Logarithmus seiner Basis.

* * *

*Übergang zu einer neuen Stiftung

* * *

Weitere Eigenschaften:

* * *

Die Berechnung von Logarithmen hängt eng mit der Verwendung von Exponenteneigenschaften zusammen.

Lassen Sie uns einige davon auflisten:

Der Kern dieser Eigenschaft besteht darin, dass sich bei der Übertragung des Zählers auf den Nenner und umgekehrt das Vorzeichen des Exponenten in das Gegenteil ändert. Zum Beispiel:

Eine Folgerung aus dieser Eigenschaft:

* * *

Bei der Potenzierung bleibt die Basis gleich, die Exponenten werden jedoch multipliziert.

* * *

Wie Sie gesehen haben, ist das Konzept eines Logarithmus selbst einfach. Die Hauptsache ist, was benötigt wird gute Übung, was eine gewisse Fähigkeit verleiht. Natürlich sind Formelkenntnisse erforderlich. Wenn die Fähigkeit zur Umrechnung elementarer Logarithmen nicht entwickelt ist, können Sie beim Lösen einfacher Aufgaben leicht einen Fehler machen.

Üben Sie, lösen Sie zunächst die einfachsten Beispiele aus dem Mathematikkurs und gehen Sie dann zu komplexeren über. In Zukunft werde ich auf jeden Fall zeigen, wie „gruselige“ Logarithmen gelöst werden; sie werden nicht im Einheitlichen Staatsexamen erscheinen, aber sie sind von Interesse, verpassen Sie sie nicht!

Das ist alles! Viel Glück!

Mit freundlichen Grüßen, Alexander Krutitskikh

P.S.: Ich wäre Ihnen dankbar, wenn Sie mir in den sozialen Netzwerken von der Seite erzählen würden.

Mit der Entwicklung der Gesellschaft und der Komplexität der Produktion entwickelte sich auch die Mathematik. Übergang vom Einfachen zum Komplexen. Von der gewöhnlichen Buchführung mit der Methode der Addition und Subtraktion mit ihrer wiederholten Wiederholung kamen wir zum Konzept der Multiplikation und Division. Die Reduzierung der wiederholten Multiplikationsoperation wurde zum Konzept der Potenzierung. Die ersten Tabellen zur Abhängigkeit von Zahlen von der Basis und zur Potenzierung wurden bereits im 8. Jahrhundert vom indischen Mathematiker Varasena erstellt. Daraus können Sie den Zeitpunkt des Auftretens von Logarithmen abzählen.

Historische Skizze

Die Wiederbelebung Europas im 16. Jahrhundert förderte auch die Entwicklung der Mechanik. T erforderte einen großen Rechenaufwand im Zusammenhang mit Multiplikation und Division mehrstellige Zahlen. Die alten Tische waren von großem Nutzen. Sie ermöglichten es, komplexe Operationen durch einfachere zu ersetzen – Addition und Subtraktion. Ein großer Fortschritt war das 1544 veröffentlichte Werk des Mathematikers Michael Stiefel, in dem er die Idee vieler Mathematiker verwirklichte. Dadurch war es möglich, Tabellen nicht nur für Abschlüsse im Formular zu verwenden Primzahlen, aber auch für beliebige rationale.

Im Jahr 1614 führte der Schotte John Napier, der diese Ideen entwickelte, erstmals den neuen Begriff „Logarithmus einer Zahl“ ein. Zur Berechnung der Logarithmen von Sinus- und Cosinuswerten sowie Tangenten wurden neue komplexe Tabellen erstellt. Dies reduzierte die Arbeit der Astronomen erheblich.

Es tauchten neue Tabellen auf, die von Wissenschaftlern drei Jahrhunderte lang erfolgreich verwendet wurden. Es ist schon viel Zeit vergangen neuer Betrieb in der Algebra erhielt es seine vollständige Form. Die Definition des Logarithmus wurde gegeben und seine Eigenschaften untersucht.

Erst im 20. Jahrhundert, mit dem Aufkommen von Taschenrechnern und Computern, gab die Menschheit die alten Tabellen auf, die im 13. Jahrhundert erfolgreich funktioniert hatten.

Heute nennen wir den Logarithmus von b zur Basis von a die Zahl x, die die Potenz von a ist, um b zu bilden. Dies wird als Formel geschrieben: x = log a(b).

Beispielsweise wäre log 3(9) gleich 2. Dies ist offensichtlich, wenn man der Definition folgt. Wenn wir 3 hoch 2 erhöhen, erhalten wir 9.

Somit legt die formulierte Definition nur eine Einschränkung fest: Die Zahlen a und b müssen reell sein.

Arten von Logarithmen

Die klassische Definition heißt reeller Logarithmus und ist eigentlich die Lösung der Gleichung a x = b. Option a = 1 ist grenzwertig und nicht von Interesse. Achtung: 1 zu jeder Potenz ist gleich 1.

Realer Wert des Logarithmus nur definiert, wenn die Basis und das Argument größer als 0 sind und die Basis nicht gleich 1 sein darf.

Besonderer Platz im Bereich der Mathematik Spielen Sie Logarithmen, die je nach Größe ihrer Basis benannt werden:

Regeln und Einschränkungen

Die grundlegende Eigenschaft von Logarithmen ist die Regel: Der Logarithmus eines Produkts ist gleich der logarithmischen Summe. log abp = log a(b) + log a(p).

Als Variante dieser Aussage gilt: log c(b/p) = log c(b) - log c(p), die Quotientenfunktion ist gleich der Differenz der Funktionen.

Aus den beiden vorherigen Regeln lässt sich leicht erkennen: log a(b p) = p * log a(b).

Weitere Eigenschaften sind:

Kommentar. Es besteht kein Grund, einen häufigen Fehler zu machen: Der Logarithmus einer Summe ist nicht gleich der Summe der Logarithmen.

Viele Jahrhunderte lang war die Berechnung eines Logarithmus eine ziemlich zeitaufwändige Aufgabe. Mathematiker verwendeten die bekannte Formel der logarithmischen Theorie der Polynomentwicklung:

ln (1 + x) = x — (x^2)/2 + (x^3)/3 — (x^4)/4 + … + ((-1)^(n + 1))*(( x^n)/n), wobei n eine natürliche Zahl größer als 1 ist, die die Genauigkeit der Berechnung bestimmt.

Logarithmen mit anderen Basen wurden unter Verwendung des Satzes über den Übergang von einer Basis zur anderen und der Eigenschaft des Logarithmus des Produkts berechnet.

Da diese Methode sehr arbeitsintensiv ist und bei der Lösung praktischer Probleme Da die Implementierung schwierig war, verwendeten wir vorkompilierte Logarithmentabellen, was die gesamte Arbeit erheblich beschleunigte.

In einigen Fällen wurden speziell entwickelte Logarithmendiagramme verwendet, die eine geringere Genauigkeit lieferten, aber die Suche nach dem gewünschten Wert erheblich beschleunigten. Die über mehrere Punkte konstruierte Kurve der Funktion y = log a(x) ermöglicht es Ihnen, mit einem regulären Lineal den Wert der Funktion an jedem anderen Punkt zu ermitteln. Ingenieure lange Zeit Für diese Zwecke wurde sogenanntes Millimeterpapier verwendet.

Im 17. Jahrhundert erschienen die ersten analogen Hilfsrechenbedingungen, die 19. Jahrhundert ein fertiges Aussehen erhalten. Das erfolgreichste Gerät hieß Rechenschieber. Trotz der Einfachheit des Geräts beschleunigte sein Aussehen den Prozess aller technischen Berechnungen erheblich, und das kann kaum überschätzt werden. Derzeit sind nur wenige Menschen mit diesem Gerät vertraut.

Das Aufkommen von Taschenrechnern und Computern machte den Einsatz anderer Geräte sinnlos.

Gleichungen und Ungleichungen

Um verschiedene Gleichungen und Ungleichungen mithilfe von Logarithmen zu lösen, werden die folgenden Formeln verwendet:

• Übergang von einer Basis zur anderen: log a(b) = log c(b) / log c(a);
• Als Konsequenz aus der vorherigen Option: log a(b) = 1 / log b(a).

Um Ungleichungen zu lösen, ist es nützlich zu wissen:

• Der Wert des Logarithmus ist nur dann positiv, wenn Basis und Argument beide größer oder kleiner als eins sind; Wenn mindestens eine Bedingung verletzt ist, ist der Logarithmuswert negativ.
• Wenn die Logarithmusfunktion auf die rechte und linke Seite einer Ungleichung angewendet wird und die Basis des Logarithmus größer als eins ist, bleibt das Vorzeichen der Ungleichung erhalten; sonst ändert es sich.

Beispiele für Probleme

Betrachten wir mehrere Möglichkeiten zur Verwendung von Logarithmen und ihren Eigenschaften. Beispiele zum Lösen von Gleichungen:

Erwägen Sie die Möglichkeit, den Logarithmus in eine Potenz zu bringen:

• Aufgabe 3. Berechnen Sie 25^log 5(3). Lösung: Unter den Bedingungen des Problems ähnelt der Eintrag dem folgenden (5^2)^log5(3) oder 5^(2 * log 5(3)). Schreiben wir es anders: 5^log 5(3*2), oder das Quadrat einer Zahl als Funktionsargument kann als Quadrat der Funktion selbst geschrieben werden (5^log 5(3))^2. Unter Verwendung der Eigenschaften von Logarithmen entspricht dieser Ausdruck 3^2. Antwort: Als Ergebnis der Berechnung erhalten wir 9.

Praktischer Nutzen

Da es sich um ein rein mathematisches Werkzeug handelt, scheint es weit davon entfernt zu sein wahres Leben dass der Logarithmus plötzlich annahm sehr wichtig um Objekte der realen Welt zu beschreiben. Es ist schwierig, eine Wissenschaft zu finden, in der sie nicht genutzt wird. Dies gilt in vollem Umfang nicht nur für natürliche, sondern auch für humanitäre Wissensgebiete.

Logarithmische Abhängigkeiten

Hier einige Beispiele für numerische Abhängigkeiten:

Mechanik und Physik

Historisch gesehen haben sich Mechanik und Physik immer mit Hilfe entwickelt mathematische Methoden Forschung und diente gleichzeitig als Anstoß für die Entwicklung der Mathematik, einschließlich der Logarithmen. Die Theorie der meisten Gesetze der Physik ist in der Sprache der Mathematik verfasst. Lassen Sie uns nur zwei Beispiele für die Beschreibung physikalischer Gesetze mit dem Logarithmus geben.

Das Problem der Berechnung einer so komplexen Größe wie der Raketengeschwindigkeit kann mithilfe der Tsiolkovsky-Formel gelöst werden, die den Grundstein für die Theorie der Weltraumforschung legte:

V = I * ln (M1/M2), wobei

• V ist die Endgeschwindigkeit des Flugzeugs.
• I – spezifischer Impuls des Motors.
• M 1 – Anfangsmasse der Rakete.
• M 2 – Endmasse.

Ein weiteres wichtiges Beispiel- Dies wird in der Formel eines anderen großen Wissenschaftlers, Max Planck, verwendet, die zur Bewertung des Gleichgewichtszustands in der Thermodynamik dient.

S = k * ln (Ω), wobei

• S – thermodynamische Eigenschaft.
• k – Boltzmann-Konstante.
• Ω ist das statistische Gewicht verschiedener Zustände.

Chemie

Weniger offensichtlich ist die Verwendung von Formeln in der Chemie, die das Verhältnis von Logarithmen enthalten. Nennen wir nur zwei Beispiele:

• Nernst-Gleichung, der Zustand des Redoxpotentials des Mediums im Verhältnis zur Aktivität von Stoffen und der Gleichgewichtskonstante.
• Auch die Berechnung von Konstanten wie dem Autolyseindex und dem Säuregehalt der Lösung ist ohne unsere Funktion nicht möglich.

Psychologie und Biologie

Und es ist überhaupt nicht klar, was Psychologie damit zu tun hat. Es stellt sich heraus, dass die Stärke der Empfindung durch diese Funktion gut als das umgekehrte Verhältnis des Reizintensitätswerts zum niedrigeren Intensitätswert beschrieben wird.

Nach den obigen Beispielen ist es nicht mehr verwunderlich, dass das Thema Logarithmen in der Biologie weit verbreitet ist. Über biologische Formen, die logarithmischen Spiralen entsprechen, könnten ganze Bände geschrieben werden.

Andere Gebiete

Es scheint, dass die Existenz der Welt ohne Verbindung mit dieser Funktion unmöglich ist, und sie unterliegt allen Gesetzen. Vor allem, wenn die Naturgesetze mit geometrischem Verlauf verbunden sind. Es lohnt sich, einen Blick auf die MatProfi-Website zu werfen, dort gibt es viele solcher Beispiele die folgenden Bereiche Aktivitäten:

Die Liste kann endlos sein. Wenn Sie die Grundprinzipien dieser Funktion beherrschen, können Sie in die Welt der unendlichen Weisheit eintauchen.

Der Schwerpunkt dieses Artikels liegt Logarithmus. Hier geben wir eine Definition eines Logarithmus, zeigen die akzeptierte Schreibweise, geben Beispiele für Logarithmen und sprechen über natürliche und dezimale Logarithmen. Anschließend betrachten wir die grundlegende logarithmische Identität.

Seitennavigation.

Definition von Logarithmus

Das Konzept eines Logarithmus entsteht bei der Lösung eines Problems in einem bestimmten umgekehrten Sinne, wenn Sie einen Exponenten aus einem bekannten Exponentenwert und einer bekannten Basis ermitteln müssen.

Aber genug Vorworte, es ist Zeit, die Frage zu beantworten: „Was ist ein Logarithmus?“ Geben wir die entsprechende Definition.

Definition.

Logarithmus von b zur Basis a, wobei a>0, a≠1 und b>0 der Exponent ist, auf den Sie die Zahl a erhöhen müssen, um als Ergebnis b zu erhalten.

An dieser Stelle stellen wir fest, dass das gesprochene Wort „Logarithmus“ sofort zwei Folgefragen aufwerfen sollte: „Welche Zahl“ und „Auf welcher Basis“. Mit anderen Worten: Es gibt einfach keinen Logarithmus, sondern nur den Logarithmus einer Zahl zu einer Basis.

Lasst uns gleich einsteigen Logarithmus-Notation: Der Logarithmus einer Zahl b zur Basis a wird normalerweise als log a b bezeichnet. Der Logarithmus einer Zahl b zur Basis e und der Logarithmus zur Basis 10 haben ihre eigenen Sonderbezeichnungen lnb bzw. logb, das heißt, sie schreiben nicht log e b, sondern lnb und nicht log 10 b, sondern lgb.

Jetzt können wir geben: .
Und die Aufzeichnungen machen keinen Sinn, da im ersten von ihnen unter dem Vorzeichen des Logarithmus steht eine negative Zahl, im zweiten gibt es eine negative Zahl in der Basis und im dritten gibt es eine negative Zahl unter dem Logarithmuszeichen und eine Einheit in der Basis.

Jetzt lasst uns darüber reden Regeln zum Lesen von Logarithmen. Log a b wird als „der Logarithmus von b zur Basis a“ gelesen. Beispielsweise ist log 2 3 der Logarithmus von drei zur Basis 2 und der Logarithmus von zwei Komma zwei Dritteln zur Basis 2 Quadratwurzel von fünf. Der Logarithmus zur Basis e heißt natürlicher Logarithmus, und die Notation lnb lautet „natürlicher Logarithmus von b“. Zum Beispiel ist ln7 der natürliche Logarithmus von sieben, und wir werden ihn als natürlichen Logarithmus von Pi lesen. Der Logarithmus zur Basis 10 hat auch einen besonderen Namen – dezimaler Logarithmus, und lgb wird als „dezimaler Logarithmus von b“ gelesen. Beispielsweise ist lg1 der dezimale Logarithmus von eins und lg2,75 der dezimale Logarithmus von zwei Komma sieben fünf Hundertstel.

Es lohnt sich, gesondert auf die Bedingungen a>0, a≠1 und b>0 einzugehen, unter denen die Definition des Logarithmus gegeben ist. Lassen Sie uns erklären, woher diese Einschränkungen kommen. Eine Gleichheit der Form namens , die sich direkt aus der oben gegebenen Definition des Logarithmus ergibt, wird uns dabei helfen.

Beginnen wir mit a≠1. Da eins hoch zu jeder Potenz gleich eins ist, kann die Gleichheit nur dann wahr sein, wenn b=1, aber log 1 1 kann jede reelle Zahl sein. Um diese Mehrdeutigkeit zu vermeiden, wird a≠1 angenommen.

Begründen wir die Zweckmäßigkeit der Bedingung a>0. Mit a=0 hätten wir nach der Definition eines Logarithmus eine Gleichheit, die nur mit b=0 möglich ist. Aber dann kann log 0 0 jede reelle Zahl ungleich Null sein, da Null zu jeder Potenz ungleich Null Null ist. Die Bedingung a≠0 ermöglicht es uns, diese Mehrdeutigkeit zu vermeiden. Und wenn a<0 нам бы пришлось отказаться от рассмотрения рациональных и иррациональных значений логарифма, так как степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Поэтому и принимается условие a>0 .

Schließlich folgt aus der Ungleichung a>0 die Bedingung b>0, da , und der Wert einer Potenz mit positiver Basis a immer positiv ist.

Um diesen Punkt abzuschließen, nehmen wir an, dass die angegebene Definition des Logarithmus es Ihnen ermöglicht, den Wert des Logarithmus sofort anzugeben, wenn die Zahl unter dem Logarithmuszeichen eine bestimmte Potenz der Basis ist. Tatsächlich erlaubt uns die Definition eines Logarithmus zu sagen, dass, wenn b=ap, dann der Logarithmus der Zahl b zur Basis a gleich p ist. Das heißt, das Gleichheitsprotokoll a a p =p ist wahr. Wir wissen zum Beispiel, dass 2 3 =8, dann ist log 2 8=3. Wir werden im Artikel mehr darüber sprechen.

Definition von Logarithmus

Der Logarithmus von b zur Basis a ist der Exponent, auf den a erhöht werden muss, um b zu erhalten.

Nummer e In der Mathematik ist es üblich, die Grenze zu bezeichnen, bis zu der ein Ausdruck strebt

Nummer e Ist irrationale Zahl- eine mit eins inkommensurable Zahl, die weder als ganze Zahl noch als Bruch genau ausgedrückt werden kann rational Nummer.

Buchstabe e- erster Buchstabe eines lateinischen Wortes exponieren- angeben, daher der Name in der Mathematik exponentiell- Exponentialfunktion.

Nummer e weit verbreitet in der Mathematik und in allen Wissenschaften, die auf die eine oder andere Weise mathematische Berechnungen für ihre Zwecke nutzen.

Logarithmen. Eigenschaften von Logarithmen

Definition: Der Logarithmus einer positiven Zahl b zu ihrer Basis ist der Exponent c, um den die Zahl a erhöht werden muss, um die Zahl b zu erhalten.

Grundlegende logarithmische Identität:

7) Formel für den Umzug in eine neue Basis:

lna = log e a, e ≈ 2,718…

Aufgaben und Tests zum Thema „Logarithmen. Eigenschaften von Logarithmen"

• Logarithmen – Wichtige Themen zur Prüfung des Einheitlichen Staatsexamens in Mathematik

Um Aufgaben zu diesem Thema erfolgreich abzuschließen, müssen Sie die Definition eines Logarithmus, die Eigenschaften von Logarithmen, die grundlegende logarithmische Identität sowie die Definitionen von Dezimal- und natürlichen Logarithmen kennen. Die Hauptaufgabentypen zu diesem Thema sind Probleme bei der Berechnung und Transformation logarithmischer Ausdrücke. Betrachten wir ihre Lösung anhand der folgenden Beispiele.

Lösung: Mit den Eigenschaften von Logarithmen erhalten wir

Lösung: Unter Verwendung der Eigenschaften von Graden erhalten wir

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Eigenschaften von Logarithmen, Formulierungen und Beweisen.

Logarithmen haben eine Reihe charakteristischer Eigenschaften. In diesem Artikel werden wir uns mit den wichtigsten befassen Eigenschaften von Logarithmen. Hier geben wir ihre Formulierungen an, schreiben die Eigenschaften von Logarithmen in Form von Formeln nieder, zeigen Beispiele für ihre Anwendung und führen auch Beweise für die Eigenschaften von Logarithmen.

Seitennavigation.

Grundlegende Eigenschaften von Logarithmen, Formeln

Um es einfacher zu merken und zu verwenden, stellen wir es uns vor Grundeigenschaften von Logarithmen in Form einer Liste von Formeln. Im nächsten Absatz geben wir deren Formulierungen, Belege, Anwendungsbeispiele und notwendige Erläuterungen.

Eigenschaft des Logarithmus der Einheit: log a 1=0 für jedes a>0, a≠1.

Logarithmus einer Zahl gleich der Basis: log a a=1 für a>0, a≠1.

Eigenschaft des Logarithmus der Potenz der Basis: log a a p =p, wobei a>0, a≠1 und p eine beliebige reelle Zahl ist.

Logarithmus des Produkts zweier positiver Zahlen: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
und die Eigenschaft des Logarithmus des Produkts von n positiven Zahlen: log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n , a>0 , a≠1 , x 1 >0, x 2 >0, …, x n >0 .

Eigenschaft des Logarithmus eines Quotienten: , wobei a>0, a≠1, x>0, y>0.

Logarithmus der Potenz einer Zahl: log a b p =p·log a |b| , wobei a>0, a≠1, b und p Zahlen sind, so dass der Grad b p sinnvoll ist und b p > 0.

Folge: , wobei a>0, a≠1, n eine natürliche Zahl größer als eins ist, b>0.

Folgerung 1: , a>0 , a≠1 , b>0 , b≠1 .

Folgerung 2: , a>0 , a≠1 , b>0 , p und q sind reelle Zahlen, q≠0 , insbesondere für b=a gilt .

Formulierungen und Eigenschaftsnachweise

Wir fahren mit der Formulierung und dem Beweis der schriftlichen Eigenschaften von Logarithmen fort. Alle Eigenschaften von Logarithmen werden anhand der Definition des Logarithmus und der daraus folgenden logarithmischen Grundidentität sowie der Eigenschaften des Grades bewiesen.

Lass uns beginnen mit Eigenschaften des Logarithmus von Eins. Seine Formulierung lautet wie folgt: Logarithmus der Einheit gleich Null, also, log a 1=0 für jedes a>0, a≠1. Der Beweis ist nicht schwierig: Da a 0 =1 für jedes a, das die oben genannten Bedingungen a>0 und a≠1 erfüllt, folgt der zu beweisende Gleichheitslog a 1=0 unmittelbar aus der Definition des Logarithmus.

Geben wir Beispiele für die Anwendung der betrachteten Eigenschaft: log 3 1=0, log1=0 und .

Kommen wir zur nächsten Eigenschaft: Der Logarithmus einer Zahl gleich der Basis ist gleich eins, also, log a a=1 für a>0, a≠1. Da a 1 =a für jedes a gilt, ist nach Definition des Logarithmus log a a=1.

Beispiele für die Verwendung dieser Eigenschaft von Logarithmen sind die Gleichungen log 5 5=1, log 5,6 5,6 und lne=1.

Der Logarithmus einer Potenz einer Zahl gleich der Basis des Logarithmus ist gleich dem Exponenten. Diese Eigenschaft des Logarithmus entspricht einer Formel der Form log a a p =p, wobei a>0, a≠1 und p – eine beliebige reelle Zahl. Diese Eigenschaft folgt direkt aus der Definition des Logarithmus. Beachten Sie, dass Sie damit den Wert des Logarithmus sofort angeben können. Wenn es möglich ist, die Zahl unter dem Logarithmuszeichen als Potenz der Basis darzustellen, werden wir im Artikel „Logarithmen berechnen“ näher darauf eingehen.

Zum Beispiel log 2 2 7 =7, log10 -4 =-4 und .

Logarithmus des Produkts zweier positiver Zahlen x und y ist gleich dem Produkt der Logarithmen dieser Zahlen: log a (x y)=log a x+log a y, a>0 , a≠1 . Beweisen wir die Eigenschaft des Logarithmus eines Produkts. Aufgrund der Eigenschaften des Grades a log a x+log a y =a log a x ·a log a y, und da durch die logarithmische Hauptidentität a log a x =x und a log a y =y, dann a log a x ·a log a y =x·y. Somit ist ein log a x+log a y =x·y, woraus nach der Definition eines Logarithmus die zu beweisende Gleichheit folgt.

Lassen Sie uns Beispiele für die Verwendung der Eigenschaft des Logarithmus eines Produkts zeigen: log 5 (2 3)=log 5 2+log 5 3 und .

Die Eigenschaft des Logarithmus eines Produkts lässt sich auf das Produkt einer endlichen Zahl n positiver Zahlen x 1 , x 2 , …, x n as verallgemeinern log a (x 1 · x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n. Mit der Methode der mathematischen Induktion lässt sich diese Gleichheit problemlos beweisen.

Beispielsweise kann der natürliche Logarithmus des Produkts durch die Summe dreier natürlicher Logarithmen der Zahlen 4, e und ersetzt werden.

Logarithmus des Quotienten zweier positiver Zahlen x und y ist gleich der Differenz zwischen den Logarithmen dieser Zahlen. Die Eigenschaft des Logarithmus eines Quotienten entspricht einer Formel der Form , wobei a>0, a≠1, x und y einige positive Zahlen sind. Die Gültigkeit dieser Formel ist ebenso bewiesen wie die Formel für den Logarithmus eines Produkts: seit , dann per Definition des Logarithmus .

Hier ist ein Beispiel für die Verwendung dieser Eigenschaft des Logarithmus: .

Lass uns weitergehen zu Eigenschaft des Logarithmus der Potenz. Der Logarithmus eines Grades ist gleich dem Produkt aus dem Exponenten und dem Logarithmus des Basismoduls dieses Grades. Schreiben wir diese Eigenschaft des Logarithmus einer Potenz als Formel: log a b p =p·log a |b|, wobei a>0, a≠1, b und p Zahlen sind, so dass der Grad b p sinnvoll ist und b p > 0.

Zuerst beweisen wir, dass diese Eigenschaft positiv b ist. Die grundlegende logarithmische Identität ermöglicht es uns, die Zahl b als a log a b darzustellen, dann ist b p =(a log a b) p , und der resultierende Ausdruck ist aufgrund der Potenzeigenschaft gleich a p·log a b . Wir kommen also zu der Gleichung b p =a p·log a b, woraus wir durch die Definition eines Logarithmus schließen, dass log a b p =p·log a b.

Es bleibt noch, diese Eigenschaft für negatives b zu beweisen. Hier stellen wir fest, dass der Ausdruck log a b p für negatives b nur für gerade Exponenten p sinnvoll ist (da der Wert des Grades b p größer als Null sein muss, sonst ergibt der Logarithmus keinen Sinn) und in diesem Fall b p =|b| P. Dann ist b p =|b| p =(a log a |b|) p =a p·log a |b| , woraus log a b p =p·log a |b| .

Zum Beispiel, und ln(-3) 4 =4·ln|-3|=4·ln3 .

Es folgt aus der vorherigen Eigenschaft Eigenschaft des Logarithmus von der Wurzel: Der Logarithmus der n-ten Wurzel ist gleich dem Produkt des Bruchs 1/n mit dem Logarithmus des Wurzelausdrucks, d. h. wenn a>0, a≠1, n eine natürliche Zahl größer als eins ist, b>0 .

Der Beweis basiert auf der Gleichheit (siehe Definition des Exponenten mit einem gebrochenen Exponenten), die für jedes positive b gilt, und der Eigenschaft des Logarithmus des Exponenten: .

Hier ist ein Beispiel für die Verwendung dieser Eigenschaft: .

Jetzt lasst uns beweisen Formel für den Übergang zu einer neuen Logarithmusbasis Typ . Dazu reicht es aus, die Gültigkeit der Gleichheit log c b=log a b·log c a zu beweisen. Die grundlegende logarithmische Identität ermöglicht es uns, die Zahl b als log a b darzustellen, dann log c b=log c a log a b . Es bleibt noch die Eigenschaft des Logarithmus des Grades zu verwenden: log c a log a b =log a b·log c a . Damit ist die Gleichheit log c b=log a b·log c a bewiesen, was bedeutet, dass auch die Formel für den Übergang zu einer neuen Basis des Logarithmus bewiesen ist .

Lassen Sie uns einige Beispiele für die Verwendung dieser Eigenschaft von Logarithmen zeigen: und .

Die Formel für den Wechsel zu einer neuen Basis ermöglicht es Ihnen, mit Logarithmen zu arbeiten, die eine „bequeme“ Basis haben. Beispielsweise kann damit auf natürliche oder dezimale Logarithmen umgestellt werden, sodass Sie den Wert eines Logarithmus aus einer Logarithmentabelle berechnen können. Die Formel zum Wechseln zu einer neuen Logarithmusbasis ermöglicht es in einigen Fällen auch, den Wert eines bestimmten Logarithmus zu ermitteln, wenn die Werte einiger Logarithmen mit anderen Basen bekannt sind.

Ein Sonderfall der Formel für den Übergang zu einer neuen Logarithmusbasis für c=b der Form wird häufig verwendet. Dies zeigt, dass log a b und log b a zueinander inverse Zahlen sind. Z.B, .

Die Formel wird auch häufig verwendet, was zum Ermitteln der Werte von Logarithmen praktisch ist. Um unsere Worte zu bestätigen, zeigen wir, wie man damit den Wert eines Logarithmus der Form berechnen kann. Wir haben . Um die Formel zu beweisen, reicht es aus, die Formel zum Übergang zu einer neuen Basis des Logarithmus a zu verwenden: .

Es bleibt noch, die Eigenschaften des Vergleichs von Logarithmen zu beweisen.

Lassen Sie uns die umgekehrte Methode verwenden. Angenommen, für a 1 >1, a 2 >1 und a 1 2 und für 0 1 gilt log a 1 b≤log a 2 b. Basierend auf den Eigenschaften von Logarithmen können diese Ungleichungen umgeschrieben werden als Und und daraus folgt, dass log b a 1 ≤log b a 2 bzw. log b a 1 ≥log b a 2. Dann müssen entsprechend den Eigenschaften von Potenzen mit gleichen Basen die Gleichungen b log b a 1 ≥b log b a 2 und b log b a 1 ≥b log b a 2 gelten, also a 1 ≥a 2 . Wir kamen also zu einem Widerspruch zur Bedingung a 1 2. Damit ist der Beweis abgeschlossen.

Grundlegende Eigenschaften von Logarithmen

• Materialien für den Unterricht
• Laden Sie alle Formeln herunter

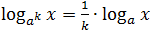
Logarithmen können wie alle Zahlen auf jede Art addiert, subtrahiert und transformiert werden. Da es sich bei Logarithmen aber nicht gerade um gewöhnliche Zahlen handelt, gibt es hier Regeln, die man nennt Haupteigenschaften.

Diese Regeln müssen Sie unbedingt kennen – ohne sie lässt sich kein einziges ernstes logarithmisches Problem lösen. Darüber hinaus gibt es nur sehr wenige davon – Sie können alles an einem Tag lernen. Also lasst uns anfangen.

Logarithmen addieren und subtrahieren

Betrachten Sie zwei Logarithmen mit denselben Basen: log a x und log a y. Dann können sie addiert und subtrahiert werden und:

Die Summe der Logarithmen ist also gleich dem Logarithmus des Produkts und die Differenz ist gleich dem Logarithmus des Quotienten. Bitte beachten Sie: Der entscheidende Punkt hier ist identische Gründe. Wenn die Gründe unterschiedlich sind, funktionieren diese Regeln nicht!

Diese Formeln helfen Ihnen, einen logarithmischen Ausdruck zu berechnen, auch wenn seine einzelnen Teile nicht berücksichtigt werden (siehe Lektion „Was ist ein Logarithmus“). Schauen Sie sich die Beispiele an und sehen Sie:

Aufgabe. Finden Sie den Wert des Ausdrucks: log 6 4 + log 6 9.

Da Logarithmen die gleichen Basen haben, verwenden wir die Summenformel:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Aufgabe. Finden Sie den Wert des Ausdrucks: log 2 48 − log 2 3.

Die Grundlagen sind die gleichen, wir verwenden die Differenzformel:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Aufgabe. Finden Sie den Wert des Ausdrucks: log 3 135 − log 3 5.

Auch hier sind die Grundlagen dieselben, also haben wir:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Wie Sie sehen, bestehen die ursprünglichen Ausdrücke aus „schlechten“ Logarithmen, die nicht separat berechnet werden. Aber nach den Transformationen erhält man ganz normale Zahlen. Viele bauen auf dieser Tatsache auf Testpapiere. Ja, im Einheitlichen Staatsexamen werden prüfungsähnliche Ausdrücke in aller Ernsthaftigkeit (manchmal praktisch ohne Änderungen) angeboten.

Extrahieren des Exponenten aus dem Logarithmus

Jetzt machen wir die Aufgabe etwas komplizierter. Was ist, wenn die Basis oder das Argument eines Logarithmus eine Potenz ist? Dann kann der Exponent dieses Grades nach folgenden Regeln aus dem Vorzeichen des Logarithmus entnommen werden:

• log a x n = n · log a x ;
• 
• 

Es ist leicht zu erkennen, dass die letzte Regel den ersten beiden folgt. Aber es ist trotzdem besser, sich daran zu erinnern – in manchen Fällen wird es den Rechenaufwand erheblich reduzieren.

Alle diese Regeln machen natürlich Sinn, wenn die ODZ des Logarithmus beachtet wird: a > 0, a ≠ 1, x > 0. Und noch etwas: Lernen Sie, alle Formeln nicht nur von links nach rechts anzuwenden, sondern auch umgekehrt , d.h. Sie können die Zahlen vor dem Logarithmuszeichen in den Logarithmus selbst eingeben. Dies wird am häufigsten benötigt.

Aufgabe. Finden Sie den Wert des Ausdrucks: log 7 49 6 .

Lassen Sie uns den Grad im Argument loswerden, indem wir die erste Formel verwenden:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Aufgabe. Finden Sie die Bedeutung des Ausdrucks:

[Bildunterschrift]

Beachten Sie, dass der Nenner einen Logarithmus enthält, dessen Basis und Argument exakte Potenzen sind: 16 = 2 4 ; 49 = 7 2. Wir haben:

[Bildunterschrift]

Ich denke, das letzte Beispiel bedarf einer Klarstellung. Wo sind die Logarithmen geblieben? Bis zum letzten Moment arbeiten wir nur mit dem Nenner. Wir stellten die Basis und das Argument des dort stehenden Logarithmus in Form von Potenzen dar und entfernten die Exponenten – wir erhielten einen „dreistöckigen“ Bruch.

Schauen wir uns nun den Hauptbruch an. Zähler und Nenner enthalten die gleiche Zahl: log 2 7. Da log 2 7 ≠ 0 ist, können wir den Bruch kürzen – 2/4 bleiben im Nenner. Nach den Regeln der Arithmetik lässt sich die Vier auf den Zähler übertragen, was auch geschehen ist. Das Ergebnis war die Antwort: 2.

Übergang zu einer neuen Stiftung

Als ich über die Regeln zum Addieren und Subtrahieren von Logarithmen sprach, habe ich ausdrücklich betont, dass diese nur mit den gleichen Basen funktionieren. Was ist, wenn die Gründe unterschiedlich sind? Was ist, wenn es sich nicht um exakte Potenzen derselben Zahl handelt?

Hier helfen Formeln für den Übergang zu einer neuen Stiftung. Formulieren wir sie in Form eines Theorems:

Gegeben sei der Logarithmus log a x. Dann gilt für jede Zahl c mit c > 0 und c ≠ 1 die Gleichheit:

[Bildunterschrift]

Insbesondere wenn wir c = x setzen, erhalten wir:

[Bildunterschrift]

Aus der zweiten Formel folgt, dass Basis und Argument des Logarithmus vertauscht werden können, allerdings wird in diesem Fall der gesamte Ausdruck „umgedreht“, also der Logarithmus erscheint im Nenner.

Diese Formeln sind in konventionellen Formen selten zu finden numerische Ausdrücke. Wie praktisch sie sind, lässt sich nur bei der Lösung logarithmischer Gleichungen und Ungleichungen beurteilen.

Es gibt jedoch Probleme, die nur durch den Umzug in eine neue Stiftung gelöst werden können. Schauen wir uns einige davon an:

Aufgabe. Finden Sie den Wert des Ausdrucks: log 5 16 log 2 25.

Beachten Sie, dass die Argumente beider Logarithmen exakte Potenzen enthalten. Nehmen wir die Indikatoren heraus: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Lassen Sie uns nun den zweiten Logarithmus „umkehren“:

[Bildunterschrift]

Da sich das Produkt beim Umordnen der Faktoren nicht ändert, haben wir in aller Ruhe vier und zwei multipliziert und uns dann mit Logarithmen befasst.

Aufgabe. Finden Sie den Wert des Ausdrucks: log 9 100 lg 3.

Basis und Argument des ersten Logarithmus sind exakte Potenzen. Schreiben wir das auf und entfernen wir die Indikatoren:

[Bildunterschrift]

Lassen Sie uns nun den dezimalen Logarithmus loswerden, indem wir zu einer neuen Basis wechseln:

[Bildunterschrift]

Grundlegende logarithmische Identität

Im Lösungsprozess ist es oft notwendig, eine Zahl als Logarithmus zu einer gegebenen Basis darzustellen. In diesem Fall helfen uns folgende Formeln:

1. n = log a a n

2. Im ersten Fall wird die Zahl n zum Exponenten im Argument. Die Zahl n kann absolut alles sein, da es sich nur um einen Logarithmuswert handelt.

   Die zweite Formel ist eigentlich eine paraphrasierte Definition. So nennt man es: die grundlegende logarithmische Identität.

   Was passiert eigentlich, wenn die Zahl b so potenziert wird, dass die Potenz von b die Zahl a ergibt? Das ist richtig: Das Ergebnis ist die gleiche Zahl a. Lesen Sie diesen Absatz noch einmal sorgfältig durch – viele Menschen bleiben dabei hängen.

   Wie Formeln für den Übergang zu einer neuen Basis ist die grundlegende logarithmische Identität manchmal die einzig mögliche Lösung.

   [Bildunterschrift]

   Beachten Sie, dass log 25 64 = log 5 8 – wir haben einfach das Quadrat aus der Basis und dem Argument des Logarithmus gebildet. Unter Berücksichtigung der Regeln zur Potenzmultiplikation mit gleicher Basis erhalten wir:

   [Bildunterschrift]

   Falls es jemand nicht weiß, das war eine echte Aufgabe aus dem Einheitlichen Staatsexamen :)

   Logarithmische Einheit und logarithmischer Nullpunkt

   Abschließend möchte ich zwei Identitäten nennen, die kaum als Eigenschaften bezeichnet werden können – vielmehr sind sie Konsequenzen der Definition des Logarithmus. Sie tauchen ständig in Problemen auf und bereiten überraschenderweise auch „fortgeschrittenen“ Studierenden Probleme.

   1. log a a = 1 ist eine logarithmische Einheit. Denken Sie ein für alle Mal daran: Der Logarithmus zu jeder Basis a dieser Basis selbst ist gleich eins.
   2. log a 1 = 0 ist logarithmisch Null. Die Basis a kann alles sein, aber wenn das Argument eins enthält, ist der Logarithmus gleich Null! Denn a 0 = 1 ist eine direkte Folge der Definition.

   Das sind alle Eigenschaften. Üben Sie unbedingt die Umsetzung! Laden Sie den Spickzettel zu Beginn der Lektion herunter, drucken Sie ihn aus und lösen Sie die Aufgaben.

   Logarithmus. Eigenschaften des Logarithmus (Addition und Subtraktion).

   Eigenschaften des Logarithmus folgt aus seiner Definition. Und so der Logarithmus der Zahl B bezogen auf A ist definiert als der Exponent, auf den eine Zahl erhöht werden muss A um die Nummer zu bekommen B(Logarithmus existiert nur für positive Zahlen).

   Aus dieser Formulierung folgt die Berechnung x=log a b, entspricht der Lösung der Gleichung a x =b. Zum Beispiel, log 2 8 = 3 weil 8 = 2 3 . Die Formulierung des Logarithmus ermöglicht es, das Wenn zu begründen b=a c, dann der Logarithmus der Zahl B bezogen auf A gleicht Mit. Es ist auch klar, dass das Thema Logarithmen eng mit dem Thema Potenzen verbunden ist.

   Mit Logarithmen können Sie wie mit allen Zahlen umgehen Operationen der Addition, Subtraktion und auf jede erdenkliche Weise verwandeln. Da es sich bei Logarithmen jedoch nicht um ganz gewöhnliche Zahlen handelt, gelten hier eigene Sonderregeln, die man nennt Haupteigenschaften.

   Logarithmen addieren und subtrahieren.

   Nehmen wir zwei Logarithmen mit den gleichen Basen: Log ein x Und log ein y. Dann ist es möglich, Additions- und Subtraktionsoperationen durchzuführen:

   Wie wir sehen, Summe der Logarithmen entspricht dem Logarithmus des Produkts und Unterschied Logarithmen- Logarithmus des Quotienten. Darüber hinaus gilt dies, wenn die Zahlen A, X Und bei positiv und a ≠ 1.

   Es ist wichtig zu beachten, dass der Hauptaspekt dieser Formeln die gleichen Grundlagen sind. Bei abweichenden Gründen gelten diese Regeln nicht!

   Die Regeln zum Addieren und Subtrahieren von Logarithmen mit gleichen Basen werden nicht nur von links nach rechts gelesen, sondern auch umgekehrt. Als Ergebnis haben wir die Sätze für den Logarithmus des Produkts und den Logarithmus des Quotienten.

   Logarithmus des Produkts zwei positive Zahlen sind gleich der Summe ihrer Logarithmen ; Wenn wir diesen Satz umschreiben, erhalten wir Folgendes, wenn die Zahlen A, X Und bei positiv und a ≠ 1, Das:

   Logarithmus des Quotienten zwei positive Zahlen ist gleich der Differenz zwischen den Logarithmen des Dividenden und des Divisors. Anders ausgedrückt, wenn die Zahlen A, X Und bei positiv und a ≠ 1, Das:

   Wenden wir zur Lösung die obigen Theoreme an Beispiele:

   Wenn die Zahlen X Und bei sind also negativ Produktlogarithmusformel wird bedeutungslos. Daher ist es verboten zu schreiben:

   da die Ausdrücke log 2 (-8) und log 2 (-4) überhaupt nicht definiert sind (logarithmische Funktion). bei= Protokoll 2 X nur für positive Argumentwerte definiert X).

   Produktsatz nicht nur für zwei, sondern für eine unbegrenzte Anzahl von Faktoren anwendbar. Das bedeutet für jeden natürlichen k und alle positiven Zahlen X 1 , X 2 , . . . ,x n Es gibt eine Identität:

   Aus Logarithmus-Quotientensatz Eine weitere Eigenschaft des Logarithmus kann erhalten werden. Es ist allgemein bekannt, dass log A 1= 0 also

   Das heißt, es besteht eine Gleichheit:

   Logarithmen zweier reziproker Zahlen aus dem gleichen Grund werden sich nur durch das Vorzeichen voneinander unterscheiden. Also:

   Logarithmus. Eigenschaften von Logarithmen

   Logarithmus. Eigenschaften von Logarithmen

   Betrachten wir Gleichheit. Teilen Sie uns die Werte von und mit und wir möchten den Wert von ermitteln.

   Das heißt, wir suchen nach dem Exponenten, um den wir ihn spannen müssen, um zu erhalten.

   Lassen kann eine Variable jeden realen Wert annehmen, dann gelten für die Variablen folgende Einschränkungen: o" title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″ />

   Wenn wir die Werte von und kennen und vor der Aufgabe stehen, das Unbekannte zu finden, dann führen wir zu diesem Zweck ein mathematische Operation Was heisst Logarithmus.

   Um den Wert zu finden, den wir nehmen Logarithmus einer Zahl Von Basis :

   Der Logarithmus einer Zahl zur Basis ist der Exponent, auf den sie erhöht werden muss, um zu erhalten.

   Also grundlegende logarithmische Identität:

   o» title=»a>o»/> , 1″ title=»a1″/>, 0″ title=»b>0″/>

   Ist im Wesentlichen mathematische Notation Definitionen von Logarithmus.

   Die mathematische Operation des Logarithmus ist die Umkehrung der Potenzierungsoperation, also Eigenschaften von Logarithmen hängen eng mit den Eigenschaften des Grades zusammen.

   Lassen Sie uns die wichtigsten auflisten Eigenschaften von Logarithmen:

   (o" title="a>o"/> , 1″ title=»a1″/>, 0″ title=»b>0″/>, 0,

   d>0″/>, 1″ title=“d1″/>

   4.

   5.

   Mit der folgenden Gruppe von Eigenschaften können Sie den Exponenten eines Ausdrucks unter dem Vorzeichen des Logarithmus oder an der Basis des Logarithmus in Form eines Koeffizienten vor dem Vorzeichen des Logarithmus darstellen:

   6.

   7.

   8.

   9.

   Die nächste Gruppe von Formeln ermöglicht den Übergang von einem Logarithmus mit einer bestimmten Basis zu einem Logarithmus mit einer beliebigen Basis und heißt Formeln für den Umzug in eine neue Basis:

   10.

   12. (Folge aus Eigenschaft 11)

   

   Die folgenden drei Eigenschaften sind nicht allgemein bekannt, werden jedoch häufig beim Lösen logarithmischer Gleichungen oder beim Vereinfachen von Ausdrücken, die Logarithmen enthalten, verwendet:

   13.

   14.

   15.

   Sonderfälle:

   — dezimaler Logarithmus

   — natürlicher Logarithmus

   Bei der Vereinfachung von Ausdrücken, die Logarithmen enthalten, wird ein allgemeiner Ansatz verwendet:

   1. Vorstellung Dezimalstellen in Form von gewöhnlichen.

   2. Wir stellen gemischte Zahlen als unechte Brüche dar.

   3. Wir zerlegen die Zahlen zur Basis des Logarithmus und unter dem Vorzeichen des Logarithmus in einfache Faktoren.

   4. Wir versuchen, alle Logarithmen auf die gleiche Basis zu reduzieren.

   5. Wenden Sie die Eigenschaften von Logarithmen an.

   Schauen wir uns Beispiele für die Vereinfachung von Ausdrücken an, die Logarithmen enthalten.

   Beispiel 1.

   Berechnung:

   Vereinfachen wir alle Exponenten: Unsere Aufgabe besteht darin, sie auf Logarithmen zu reduzieren, deren Basis dieselbe Zahl ist wie die Basis des Exponenten.

   ==(nach Eigenschaft 7)=(nach Eigenschaft 6) =

   Ersetzen wir die Indikatoren, die wir erhalten haben, in den ursprünglichen Ausdruck. Wir bekommen:

   Antwort: 5.25

   Beispiel 2. Berechnen Sie:

   

   Reduzieren wir alle Logarithmen auf die Basis 6 (in diesem Fall „wandern“ die Logarithmen vom Nenner des Bruchs zum Zähler):

   Zerlegen wir die Zahlen unter dem Logarithmuszeichen in einfache Faktoren:

   Wenden wir die Eigenschaften 4 und 6 an:

   Lassen Sie uns den Ersatz vorstellen

   Wir bekommen:

   Antwort 1

   Logarithmus . Grundlegende logarithmische Identität.

   Eigenschaften von Logarithmen. Dezimaler Logarithmus. Natürlicher Logarithmus.

   Logarithmus positive Zahl N zur Basis (B > 0, B 1) ist der Exponent x, auf den b erhöht werden muss, um N zu erhalten .

   Dieser Eintrag entspricht dem Folgenden: b x = N .

   Beispiele: log 3 81 = 4, da 3 4 = 81;

   log 1/3 27 = – 3, da (1/3) - 3 = 3 · 3 = 27.

   Die obige Definition des Logarithmus kann als Identität geschrieben werden:

   

   Grundlegende Eigenschaften von Logarithmen.

   2) log 1 = 0, da B 0 = 1 .

   3) Der Logarithmus des Produkts ist gleich der Summe der Logarithmen der Faktoren:

   4) Der Logarithmus des Quotienten ist gleich der Differenz zwischen den Logarithmen des Dividenden und des Divisors:

   5) Der Logarithmus einer Potenz ist gleich dem Produkt aus dem Exponenten und dem Logarithmus seiner Basis:

   Die Konsequenz dieser Eigenschaft ist folgende: Logarithmus der Wurzel gleich dem Logarithmus der Wurzelzahl dividiert durch die Potenz der Wurzel:

   

   6) Wenn die Basis des Logarithmus ein Grad ist, dann der Wert Der Kehrwert des Exponenten lässt sich als Logarithmusreim darstellen:

   

   Die letzten beiden Eigenschaften können zu einer kombiniert werden:

   

   7) Übergangsmodulformel (d. h. Übergang von einer Logarithmusbasis zu einer anderen Basis):

   

   Im Sonderfall wann N=a wir haben:

   

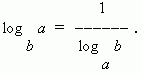
   Dezimaler Logarithmus angerufen Basislogarithmus 10. Es wird mit lg bezeichnet, d.h. Protokoll 10 N= Protokoll N. Logarithmen der Zahlen 10, 100, 1000, . p sind jeweils 1, 2, 3, …, d. h. habe so viel positives

   Einheiten, wie viele Nullen gibt es in einer logarithmischen Zahl nach einer? Logarithmen der Zahlen 0,1, 0,01, 0,001, . p sind jeweils –1, –2, –3, …, d.h. haben so viele negative Einsen, wie es Nullen in der logarithmischen Zahl vor der Eins gibt (einschließlich ganzer Nullen). Die Logarithmen anderer Zahlen haben einen sogenannten Bruchteil Mantisse. Ganzer Teil der Logarithmus heißt charakteristisch. Für den praktischen Gebrauch sind dezimale Logarithmen am praktischsten.

   Natürlicher Logarithmus angerufen Basislogarithmus e. Es wird mit ln bezeichnet, d.h. Protokoll e N= Protokoll N. Nummer e ist irrational, sein ungefährer Wert ist 2,718281828. Es ist die Grenze, zu der die Zahl tendiert (1 + 1 / N) N mit unbegrenzter Steigerung N(cm. Erste wunderbare Grenze auf der Seite „Limits“. Zahlenfolgen»).
   So seltsam es auch klingen mag, natürliche Logarithmen erwiesen sich bei der Durchführung verschiedener Arten von Operationen im Zusammenhang mit der Funktionsanalyse als sehr praktisch. Logarithmen zur Basis berechnen e viel schneller durchgeführt werden als aus irgendeinem anderen Grund.

• Wie erhalte ich eine Bescheinigung über die staatliche Registrierung des Eigentums einer Wohnung? Gemäß der Verfassung der Russischen Föderation ist der Staat mit der Funktion des Garanten privater Eigentumsrechte betraut. Die Befugnisse des Staates in diesem Bereich […]
• Ecken und Mittelpunkte in Gruppen Ecken – der Abschnitt, in dem interessante Ideen und Gestaltungsmöglichkeiten für Informations-, Entwicklungs- und Spielecken in Kindergarten, hergestellt von den Händen von Lehrern und Erziehern. IN Gruppe vorschulischer Bildungseinrichtungen abhängig von […]
• Was ist heute nötig, um in Russland ein Kind zu adoptieren? Eine Adoption in Russland erfordert neben einer verantwortungsvollen persönlichen Entscheidung eine Reihe von Verfahren zur staatlichen Überprüfung der Kandidaten. Eine strenge Auswahl in der Vorbereitungsphase trägt zu mehr […] bei.
• Strafe für die Nichteinreichung der SZV-M- und RSV-1-Meldungen an die Pensionskasse der Russischen Föderation. Am Ende jedes Melde- und Abrechnungszeitraums muss der Versicherungsnehmer der Pensionskasse die erforderliche Berechnung im RSV-1-Formular vorlegen. Wenn aus irgendeinem Grund […]
• Wann und wie erhalten Sie den kapitalgedeckten Teil Ihrer Rente von der Sberbank? Die Sberbank ist eine Partnerbank des staatlichen Pensionsfonds. Auf dieser Grundlage könnten Bürger, die sich für eine kapitalgedeckte Rente angemeldet haben, den kapitalgedeckten Teil […]
• So erhalten Sie Zahlungszuschüsse Dienstprogramme(mieten)? Gemäß der Wohnungsgesetzgebung der Russischen Föderation werden bestimmten Kategorien von Bürgern Zuschüsse für Stromrechnungen gewährt. Um mehr über das Verfahren zu erfahren, [...]
• Kostenlose Informationen zur TIN oder OGRN aus dem Steuerregister in ganz Russland – online. Informationen zur staatlichen Registrierung erhalten Sie auf dem Unified Tax Services Portal Rechtspersonen, Einzelunternehmer, […]
• Senkgrube: Sanitär- und Bauvorschriften und -vorschriften Um ein Abwassersystem in einer Datscha oder einem städtischen Gebiet zu installieren, müssen Sie nicht nur bauliche, sondern auch gesetzliche Standards befolgen. Senkgrube: Normen und Regeln für ihre Anordnung [...]